整理Matlab的神经网络工具箱实用指南.docx

整理Matlab的神经网络工具箱实用指南.docx

《整理Matlab的神经网络工具箱实用指南.docx》由会员分享，可在线阅读，更多相关《整理Matlab的神经网络工具箱实用指南.docx（31页珍藏版）》请在冰豆网上搜索。

整理Matlab的神经网络工具箱实用指南

Matlab的神经网络工具箱实用指南　　

文章摘要:

第一章是神经网络的基本介绍，第二章包括了由工具箱指定的有关网络结构和符号的基本材料以及建立神经网络的一些基本函数，例如new、init、adapt和train。

第三章以反向传播网络为例讲解了反向传播网络的原理和应用的基本过程。

第一章介绍

1．神经网络

神经网络是单个并行处理元素的集合，我们从生物学神经系统得到启发。

在自然界，网络功能主要由神经节决定，我们可以通过改变连接点的权重来训练神经网络完成特定的功能。

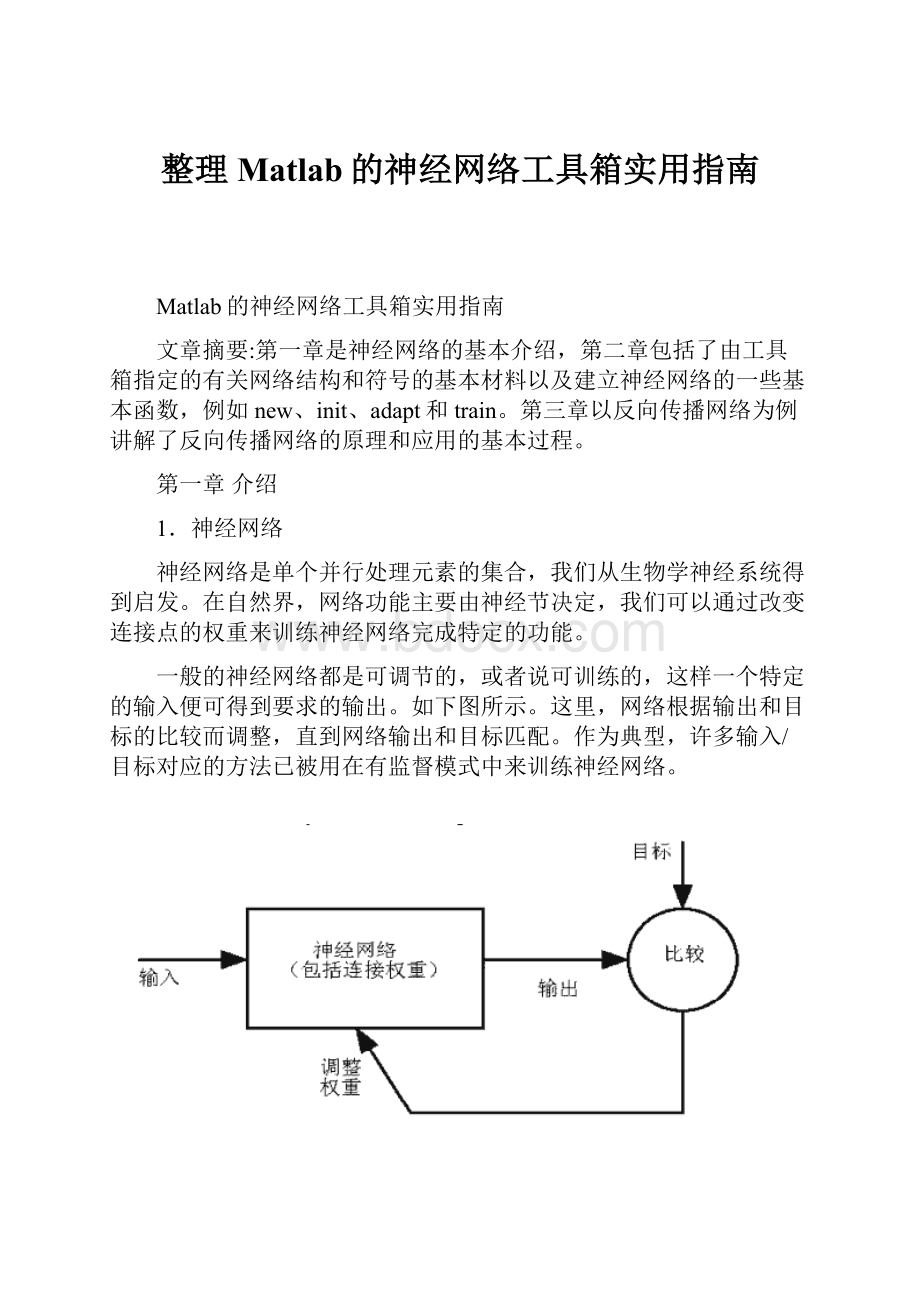
一般的神经网络都是可调节的，或者说可训练的，这样一个特定的输入便可得到要求的输出。

如下图所示。

这里，网络根据输出和目标的比较而调整，直到网络输出和目标匹配。

作为典型，许多输入/目标对应的方法已被用在有监督模式中来训练神经网络。

神经网络已经在各个领域中应用，以实现各种复杂的功能。

这些领域包括：

模式识别、鉴定、分类、语音、翻译和控制系统。

如今神经网络能够用来解决常规计算机和人难以解决的问题。

我们主要通过这个工具箱来建立示范的神经网络系统，并应用到工程、金融和其他实际项目中去。

一般普遍使用有监督训练方法，但是也能够通过无监督的训练方法或者直接设计得到其他的神经网络。

无监督网络可以被应用在数据组的辨别上。

一些线形网络和Hopfield网络是直接设计的。

总的来说，有各种各样的设计和学习方法来增强用户的选择。

神经网络领域已经有50年的历史了，但是实际的应用却是在最近15年里，如今神经网络仍快速发展着。

因此，它显然不同与控制系统和最优化系统领域，它们的术语、数学理论和设计过程都已牢固的建立和应用了好多年。

我们没有把神经网络工具箱仅看作一个能正常运行的建好的处理轮廓。

我们宁愿希望它能成为一个有用的工业、教育和研究工具，一个能够帮助用户找到什么能够做什么不能做的工具，一个能够帮助发展和拓宽神经网络领域的工具。

因为这个领域和它的材料是如此新，这个工具箱将给我们解释处理过程，讲述怎样运用它们，并且举例说明它们的成功和失败。

我们相信要成功和满意的使用这个工具箱，对范例和它们的应用的理解是很重要的，并且如果没有这些说明那么用户的埋怨和质询就会把我们淹没。

所以如果我们包括了大量的说明性材料，请保持耐心。

我们希望这些材料能对你有帮助。

这个章节在开始使用神经网络工具箱时包括了一些注释，它也描述了新的图形用户接口和新的运算法则和体系结构，并且它解释了工具箱为了使用模块化网络对象描述而增强的机动性。

最后这一章给出了一个神经网络实际应用的列表并增加了一个新的文本--神经网络设计。

这本书介绍了神经网络的理论和它们的设计和应用，并给出了相当可观的MATLAB和神经网络工具箱的使用。

2．准备工作

基本章节

第一章是神经网络的基本介绍，第二章包括了由工具箱指定的有关网络结构和符号的基本材料以及建立神经网络的一些基本函数，例如new、init、adapt和train。

第三章以反向传播网络为例讲解了反向传播网络的原理和应用的基本过程。

帮助和安装

神经网络工具箱包含在nnet目录中，键入helpnnet可得到帮助主题。

工具箱包含了许多示例。

每一个例子讲述了一个问题，展示了用来解决问题的网络并给出了最后的结果。

显示向导要讨论的神经网络例子和应用代码可以通过键入helpnndemos找到。

安装神经网络工具箱的指令可以在下列两份MATLAB文档中找到：

theInstallationGuideforMS-WindowsandMacintosh或者theInstallationGuideforUNIX。

第二章神经元模型和网络结构

1．符号

数学符号

下面给出等式和数字中用到的基本符号：

标量--小写的斜体字.....a,b,c

向量--小写加粗的非斜体字.....a,b,c

矩阵-大写加粗的非斜体字.....A,B,C

向量表示一组数字

数学符号和字符的等价

从数学符号到字符的转换或者反过来可以遵循一些规则，为了便于今后引用我们将这些规则列出。

为了从数学符号变为MATLAB符号用户需要：

变上标为细胞数组标号

例如

变下标为圆括号标号

例如

和

变圆括号标号为二维数组标号

例如

变数学运算符为MATLAB运算符和工具箱函数

例如

2．神经元模型

单神经元

下图所示为一个单标量输入且无偏置的神经元。

这个输入标量通过乘以权重为标量w的连结点得到结果wp，这仍是一个标量。

这里，加权的输入wp仅仅是转移函数f的参数，函数的输入是标量a。

右边的神经元有一个标量偏置b，你既可以认为它仅仅是通过求和节点加在结果wp上，也可以认为它把函数f左移了b个单位，偏置除了有一个固定不变的输入值1以外，其他的很像权重。

标量n是加权输入wp和偏置b的和，它作为转移函数f的参数。

函数f是转移函数，它可以为阶跃函数或者曲线函数，它接收参数n给出输出a，下一节将给出各种不同的转移函数。

注意神经元中的w和b都是可调整的标量参数。

神经网络的中心思想就是参数的可调整使得网络展示需要和令人感兴趣的行为。

这样，我们就可以通过调整权重和偏置参量训练神经网络做一定的工作。

或者神经网络自己调整参数以得到想要的结果。

在这个工具箱里所有的神经元都提供偏置，我们的许多例子中都用到了偏置并且假定它在这个工具箱的大多数情况下都要用到。

可是，如果你愿意的话，你也可以在一个神经元中省略偏置。

正如上面所提到的，在神经元中，标量b是个可调整的参数。

它不是一个输入。

可是驱动偏置的常量1却是一个输入而且当考虑线性输入向量时一定要这样认为。

转移函数

在这个工具箱里包括了许多转移函数。

你能在"TransferFunctionGraphs"中找到它们的完全列表。

下面列出了三个最常用的函数。

上图所示的阶跃转移函数限制了输出，使得输入参数小于0时输出为0，大于或等于0时输出为1，在第三章中我们将用它来进行分类。

工具箱中有一个函数hardlim来数学上的阶跃，如上图所示。

我们可以输入以下代码

n=-5:

0.1:

5;

plot（n,hardlim（n）,'c+:

'）;

它产生一张在-5到5之间的阶跃函数图。

所有在工具箱中的数学转移函数都能够用同名的函数实现。

线性转移函数如下图所示

　　这种类型的神经元将在第四章的自适应线性滤波中用作线性拟合。

　　下图显示的曲线转移函数的输入参数是正负区间的任意值，而将输出值限定于0到1之间。

　　这种传递函数通常用于反向传播（BP）网络，这得益于函数的可微性。

　　在上面所示的每一个转移函数图的右边方框中的符号代表了对应的函数，这些图表将替换网络图的方框中的f来表示所使用的特定的转移函数。

　　第13章列出了所有的转移函数和图标。

你能够定义自己的传递函数，你可以不限于使用第13章所列的转移函数。

你能够通过运行示例程序nn2n1来试验一个神经元和各种转移函数。

带向量输入的神经元

　　一个有R个元素输入向量的神经元如下图所示。

这里单个输入元素

　　乘上权重

　　得到加权值输入求和节点。

它们的和是Wp，单行矩阵W和向量p的点乘。

　　这个神经元有一个偏置b，它加在加权的输入上得到网络输入n，和值n是转移函数f的参数。

表达式自然可用MATLAB代码表示为：

n=W*p+b

　　可是，用户很少要写如此底层的代码，因为这些代码已经被建立到函数中来定义和模拟整个网络。

上面所示的图包括了许多细节。

当我们考虑有许多神经元和可能是许多神经元组成的多层网络时，我们可能会漏掉许多细节。

因此，作者设计了一个简洁的符号代表单个神经元。

这个符号如下图中所示，它将会在以后的多重神经元电路中用到。

　　这里输入向量p用左边的黑色实心竖条代表，p的维数写在符号p下面，在图中是Rx1。

（注意我们用的是大写字母，正如在以前句子里R用来表示向量大小时一样。

）因此，p是一个有R个输入元素的向量。

这个输入列向量乘上R列单行矩阵W。

和以前一样，常量1作为一个输入乘上偏置标量b，给转移函数的网络输入是n，它是偏置与乘积Wp的和。

这个和值传给转移函数f得到网络输出a，在这个例子中它是一个标量。

注意如果我们有超过一个神经元，网络输出就有可能是一个向量。

　　上面图中定义了神经网络的一层。

一层包括权重的组合，乘法和加法操作（这里就是向量乘积Wp），偏置b和转移函数f。

输入数组，即向量p不包括在一层中。

　　这个简洁的网络符号每一次都会被用到，向量的大小会显示在矩阵变量名字的下面。

我们希望这个符号会让你理解神经网络的结构以及与之相关的矩阵数学。

　　正如前面所讨论的，当特定的转移函数在一张图中被使用时，转移函数将用上面所示的符号代替。

下面是几个例子：

　　你可以通过运行示例程序nnd2n2来试验有2个元素的神经元。

　　3．网络结构

　　两个或更多的上面所示的神经元可以组合成一层，一个典型的网络可包括一层或者多层。

我们首先来研究神经元层。

　　单层神经元网络

　　有R输入元素和S个神经元组成的单层网络如下图所示：

在一个单层网络中，输入向量p的每一个元素都通过权重矩阵W和每一个神经元连接起来。

第I个神经元通过把所有加权的输入和偏置加起来得到它自己的标量输出n（i）。

不同的n（i）合起来形成了有S个元素的网络输入向量n。

最后，网络层输出一个列向量a，我们在图的底部显示了a的表达式。

注意输入元素个数R和神经元个数S通常是不等的，我们也并不需要这两者相等。

你也可以建立一个简单的复合神经元层，它将上面所示的网络并行的合在一起，使用不同的转移函数。

所有的网络都有相同的输入，而每一个网络都会产生输出。

输入向量元素经加权矩阵W作用输入网络。

W=

注意加权矩阵W的行标标记权重的目的神经元，列标标记待加权的输入标号。

因此，的标号表示从输入信号的第二个元素到第一个神经元的权重是。

有S个神经元和R个输入元素的神经网络也能够简化成以下符号：

这里，p是一个有R个元素的输入向量，W是一个SxR的矩阵，a和b是有S个元素的向量。

如前面所定义的，神经元层包括权重矩阵，乘法运算，偏置向量b，求和符和转移函数框。

输入和层

我们将要讨论多层网络，所以我们需要拓展我们的符号来描述这样的网络。

特别是我们要弄清连接输入的权重矩阵和连接层的权重矩阵之间的区别。

我们也要分清权重矩阵的目的和源。

我们将把连接输入的权重矩阵成为输入权重，把来自层输出的权重矩阵称为层矩阵。

进一步说，我们在各个权重和其他网络元素中将用上标区分源（第二个标号）和目的（第一个标号）。

作为示例，我们用简化的形式重画了上面所画的单层多输入网络。

你可以看到，我们把连接输入向量p的权重矩阵标记为输入权重矩阵（IW1,1），第二个标号1是源，第二个标号1是目的。

同样，第一层的元素，比如偏置、网络输入和输出都有上标1来表示它们属于第一层。

在下一章节，我们将用LW表示层权重矩阵，用IW表示输入权重矩阵。

你可以复习以下这一章开始的符号那一节，它把特定的网络net中用数学符号表示的层权重矩阵转换成代码，如下所示：

IW1,1net.IW{1,1}

这样,你就可以写代码来得到对转移函数的网络输入了：

n{1}=net.IW{1,1}*p+net.b{1}

多层神经元网络

一个网络可以有几层，每一层都有权重矩阵W，偏置向量b和输出向量a。

为了区分这些权重矩阵、输出矩阵等等，在图中的每一层，我们都为感兴趣的变量以上标的形式增加了层数。

你能够看到在下面所示的三层网络图和等式中使用层符号。

上面所示的网络有R1个输入，第一层有S1个神经元，第二层有S2个神经元，以次类推。

一般不同层有不同数量的神经元。

每一个神经元的偏置输入是常量1。

注意中间层的输出就是下一层的输入。

第二层可看作有S1个输入，S2个神经元和S1xS2阶权重矩阵W2的单层网络。

第二层的输入是a1，输出是a2，现在我们已经确定了第二层的所有向量和矩阵，我们就能把它看成一个单层网络了。

其他层也可以照此步骤处理。

多层网络中的层扮演着不同的角色。

给出网络输出的层叫做输出层。

所有其他的层叫做隐层。

上图所示的三层网络有一个输出层（第三层）和两个隐层（第一和第二层）。

有些作者把输入作为第四层，这里不用这种指定。

上面所示的三层网络的简洁画法如下图所示：

多层网络的功能非常强大。

举个例子，一个两层的网络，第一层的转移函数是曲线函数，第二层的转移函数是线性函数，通过训练，它能够很好的模拟任何有有限断点的函数。

这种两层网络集中应用于"反向传播网络"。

注意我们把第三层的输出a3标记为y。

我们将使用这种符号来定义这种网络的输出。

4．数据结构

这一节将讨论影响网络仿真的输入数据结构的格式。

我们首先讨论静态网络，在讨论动态网络。

我们将关心两种基本的输入向量类型：

同步（同时或者无时序）向量和异步向量。

对异步向量来说，向量的顺序是非常重要的。

对同步向量来说，顺序是不重要的，并且如果我们已经有一定数量的并行网络我们就能把一个输入向量输入到其中的任意网络。

静态网络中的同步输入仿真

仿真静态网络（没有反馈或者延迟）是网络仿真最简单的一种。

在这种情况中，我们不需要关心向量输入的时间顺序，所以我们可以认为它是同时发生的。

另外，为了是问题更简单，我们假定开始网络仅有一个输入向量。

我们用下面的网络作为例子。

为了建立这个网络我们可以用以下命令：

net=newlin（[-11;-11],1）;

简单起见我们假定权重矩阵和偏置为

W=[1，2]，b=[0]

其命令行是：

net.IW{1,1}=[12];

net.b{1}=0;

假定模拟的网络有四个无序向量，即Q=4：

这些同步向量可以用一个矩阵来表示：

P=[1223;2131];

安全评价可针对一个特定的对象，也可针对一定的区域范围。

现在我们就可以模拟这个网络了：

（四）安全预评价内容A=sim（net,P）

A=

5485

（1）可能造成重大环境影响的建设项目，编制环境影响报告书，对产生的环境影响应进行全面评价；我们向网络输入一个简单的同步向量矩阵，得到了一个简单的同步向量输出矩阵。

结果不论是由一个网络串行输出还是由四个网络并行输出得到的都是一样的。

由于输入并无关联，输入向量的顺序并不重要。

动态网络中的异步输入仿真

根据工程、系统生命周期和评价的目的，安全评价分为三类：

安全预评价、安全验收评价、安全现状评价。

当网络中存在延迟时，顺序发生的输入向量就要按一定的序列输入网络。

为了演示这种情况，我们用了一个有延迟的简单网络。

（2）辨识和分析评价对象可能存在的各种危险、有害因素，分析危险、有害因素发生作用的途径及其变化规律。

　　为了建立这个网络我们可以用以下命令：

　　net=newlin（[-11],1,[01]）;

　　net.biasConnect=0;

　　假定权重矩阵为：

　　W=[1，2]

　　命令行为：

　　net.IW{1,1}=[12];

　　假定输入顺序为：

　　p

（1）=[1],p

（2）=[2],p（3）=[3],p（4）=[4]

　　输入序列可以用一个细胞数组来表示：

　　P={1234};

　　这样我们就能模拟这个网络了：

　　A=sim（net,P）

　　A=

　　[1][4][7][10]

　　我们输入一个包含输入序列的细胞数组，网络产生一个包含输出序列的细胞数组。

注意异步输入中的输入顺序是很重要的。

在这个例子中，当前输出等于当前输入乘1加上前一个输入乘2。

如果我们改变输入顺序，那么输出结果也回随之改变。

　　动态网络中的同步输入仿真

　　如果我们在上一个例子中把输入作为同步而不是异步应用，我们就会得到完全不同的响应。

（虽然我们不清楚为什么要在动态网络中使用这种方式。

）这就好象每一个输入都同时加到一个单独的并行网络中。

在前一个例子中，如果我们用一组同步输入，我们有：

　　p1=[1],p2=[2],p3=[3],p4=[4]

　　这可用下列代码创建：

　　P=[1234];

　　模拟这个网络，我们得到：

　　A=sim（net,P）

　　A=

　　1234

　　这个结果和我们同时把每一个输入应用到单独的网络中并计算单独的输出没什么两样。

注意如果我们没有初始化延迟时间，那么缺省值就是0。

在这个例子中，由于当前输入的权重是1，输出就是输入乘1。

在某些特定的情况下，我们可能想要在同一时间模拟一些不同序列的网络响应。

这种情况我们就要给网络输入一组同步序列。

比如说，我们要把下面两个序列输入网络：

　　p

（1）=[1],p

（2）=[2],p（3）=[3],p（4）=[4]

　　p

（1）=[4],p

（2）=[3],p（3）=[2],p（4）=[1]

　　输入P应该是一个细胞数组，每一个数组元素都包含了两个同时发生的序列的元素。

　　P={[14][23][32][41]};

　　现在我们就可以模拟这个网络了：

　　A=sim（net,P）;

　　网络输出结果将是：

　　A={[14][411][78][105]}

　　你可以看到，每个矩阵的第一列是由第一组输入序列产生的输出序列，每个矩阵的第二列是由第二组输入序列产生的输出序列。

这两组序列之间没有关联，好象他们是同时应用在单个的并行网络上的。

　　下面的图表显示了当我们有Q个TS长度的序列时，在函数sim中输入P的一般格式。

它函盖了单输入向量的所有的情况。

每一个细胞数组的元素都是一个同步向量矩阵，它对应于每一个序列的同一时间点。

如果有多输入向量，那么在细胞数组中的矩阵里就有多行。

　　这一节我们我们把同步和异步输入应用到了动态网络中。

在以前的章节中我们把同步输入应用到了静态网络中。

我们也能把异步序列应用到静态网络中。

这不会改变网络的输出响应，但是这会影响训练过的网络的形式。

在下一节你会更清楚的了解这一点。

　　5．训练方式

　　在这一节中，我们将描述两种不同的训练方式。

在增加方式中，每提交一次输入数据，网络权重和偏置都更新一次。

在批处理方式中，仅仅当所有的输入数据都被提交以后，网络权重和偏置才被更新。

　　增加方式（应用与自适应网络和其他网络）

　　虽然增加方式更普遍的应用于动态网络，比如自适应滤波，但是在静态和动态网络中都可以应用它。

在这一节中我们将示范怎样把增加方式应用到这两种网络中去。

　　静态网络中的增加方式

　　继续考虑前面用过的第一个静态网络的例子，我们用增加方式来训练它，这样每提交一次输入数据，网络权重和偏置都更新一次。

在这个例子里我们用函数adapt，并给出输入和目标序列：

　　假定我们要训练网络建立以下线性函数：

　　t=2p1+p2

　　我们以前用的输入是：

　　目标输出是：

　　t1=[4],t2=[5],t3=[7],t4=[7]

　　我们首先用0初始化权重和偏置。

为了显示增加方式的效果，我们把学习速度也设为0。

　　net=newlin（[-11;-11],1,0,0）;

　　net.IW{1,1}=[00];

　　net.b{1}=0;

　　为了用增加方式，我们把输入和目标输出表示为以下序列：

　　P={[1;2][2;1][2;3][3;1]};

　　T={4577};

　　前面的讨论中，不论是作为一个同步向量矩阵输入还是作为一个异步向量细胞数组输入，模拟的输出值是一样的。

而在训练网络时，这是不对的。

当我们使用adapt函数时，如果输入是异步向量细胞数组，那么权重将在每一组输入提交的时候更新（就是增加方式），我们将在下一节看到，如果输入是同步向量矩阵，那么权重将只在所有输入提交的时候更新（就是批处理方式）。

　　我们现在开始用增加方式训练网络：

　　[net,a,e,pf]=adapt（net,P,T）;

　　由于学习速度为0，网络输出仍然为0，并且权重没有被更新。

错误和目标输出相等。

　　a=[0][0][0][0]

　　e=[4][5][7][7]

　　如果我们设置学习速度为0.1，我们就能够看到当每一组输入提交时，网络是怎么调整的了。

　　net.inputWeights{1,1}.learnParam.lr=0.1;

　　net.biases{1,1}.learnParam.lr=0.1;

　　[net,a,e,pf]=adapt（net,P,T）;

　　a=[0][2][6.0][5.8]

　　e=[4][3][1.0][1.2]

　　由于在第一个输入数据提交前还没有更新，第一个输出和学习速率为0时一样。

由于权重已更新，第二个输出就不一样了。

每计算一次错误，权重都不断的修改。

如果网络可行并且学习速率设置得当，错误将不断的趋向于0。

　　动态网络中的增加方式

　　我们同样也能用增加方式训练动态网络。

实际上，这是最普遍的情况。

让我们用前面用过的那个有输入延迟的线性网络作为例子，我们将初始化权重为0，并把学习速率设为0.1。

　　net=newlin（[-11],1,[01],0.1）;

　　net.IW{1,1}=[00];

　　net.biasConnect=0;

　　为了用增加方式，我们把输入和目标输出表示为细胞数组的元素：

　　Pi={1};

　　P={234};

　　T={357};

　　这里我们尝试训练网络把当前输入和前一次输入加起来作为当前输出。

输入序列和我们以前使用sim的例子中用过的一样，除了我们指定了输入序列的第一组作为延迟的初始状态。

现在我们可以用adapt来训练网络了：

　　[net,a,e,pf]=adapt（net,P,T,Pi）;

　　a=[0][2.4][7.98]

　　e=[3][2.6][-1.98]

　　由于权重没有更新，第一个输出是0。

每一个序列步进，权重都改变一次。

　　批处理方式

　　在批处理方式中，仅仅当所有的输入数据都被提交以后，网络权重和偏置才被更新，它也可以应用于静态和动态网络。

我们将在这一节讨论这两种类型。

静态网络中的批处理方式

2.环境影响评价工作等级的划分依据批处理方式可以用adapt或train函数来实现，虽然由于由于采用了更高效的学习算法，train通常是最好的选择。

增加方式只能用adapt来实现，train函数只能用于批处理方式。

　　让我们用前面用过的静态网络的例子开始，学习速率设置为0.1。

　　net=newlin（[-11;-11],1,0,0.1）;

　　net.IW{1,1}=[00];

　　net.b{1}=0;

　　用adapt函数实现静态网络的批处理方式，输入向量必须用同步向量矩阵的方式放置：

　　P=[1223;2131];

　　T=[4577];

　　当我们调用adapt时将触发adaptwb函数，这是缺省的线性网络调整函数。

learnwh是缺省的权重和偏置学习函数。

因此，Widrow-Hoff学习法将会被使用：

　　[net,a,e,pf]=adapt（net,P,T）;

　　a=0000

　　e=4577

　　注意网络的输出全部为0，因为在所有要训练的数据提交前