初中数学九年级中考复习圆习题课PPT.ppt

初中数学九年级中考复习圆习题课PPT.ppt

《初中数学九年级中考复习圆习题课PPT.ppt》由会员分享，可在线阅读，更多相关《初中数学九年级中考复习圆习题课PPT.ppt（85页珍藏版）》请在冰豆网上搜索。

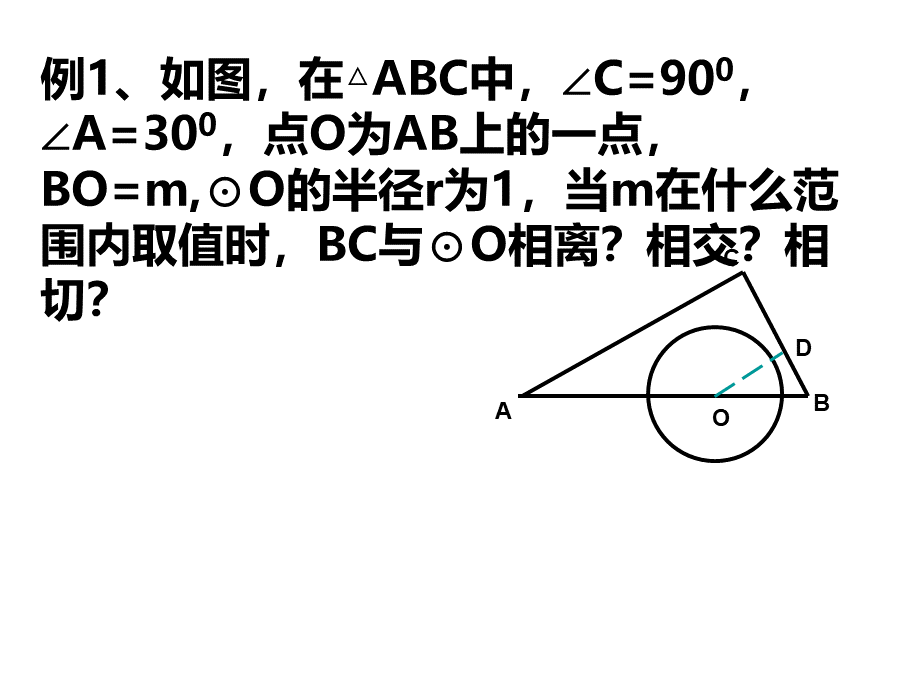
例1、如图，在ABC中，C=900，A=300，点O为AB上的一点，BO=m,O的半径r为1，当m在什么范围内取值时，BC与O相离？

相交？

相切？

A,B,C,O,D,如图，在以O为圆心的两个同心圆中，大圆的弦AB和CD相等，且AB与小圆相切于点E，求证：

CD与小圆相切。

例2O的直径AB=4,ABC=300,BC=,D是线段BC的中点，

（1）试判断点D与O的位置关系，说明理由；

（2）过点D作DE丄AC,垂足为点E,求证：

直线DE是O切线。

F,C,B,A,O,300,2,E,O,D,证明一条直线是圆的切线主要有两种方法：

一、已知待证直线经过圆上一点，那么只需证明待证直线与过圆上此点的直径（或半径）垂直；二、未知待证直线与过圆有交点，则可过圆心作直线的垂线，再证垂线段长等于半径。

F,B,.O,C,A,如上图，ABC中A=900，AB=3，BC=4，试求ABC内切圆的半径,例3：

如图,在ABC中，ACB=900，O是它的内切圆，E、D是切点，已知BOC=1050，O的半径是1，求AE的长。

A,B,C,D,E,O.,例4如图，P经过坐标原点O且与两坐标轴的正半轴交于点A，B两点，点A的坐标为（1，0），C为P上一点，且在第二象限内，AC交y轴于点D，若BC=CO=OA，以直线AB为对称轴，对ABC作轴对称变换，点C的对应点为E。

（1）求点B，点D的坐标。

（2）判断四边形A0BE是哪种特殊四边形？

并求出点E的坐标。

P,O,E,D,C,B,A（1，0）,例4如图，P经过坐标原点O且与两坐标轴的正半轴交于点A，B两点，点A的坐标为（1，0），C为P上一点，且在第二象限内，AC交y轴于点D，若BC=CO=OA，以直线AB为对称轴，对ABC作轴对称变换，点C的对应点为E。

P,O,E,D,C,B,A（1，0）,（3）求以点D为顶点，且经过点E的抛物线的函数解析式。

例4如图，P经过坐标原点O且与两坐标轴的正半轴交于点A，B两点，点A的坐标为（1，0），C为P上一点，且在第二象限内，AC交y轴于点D，若BC=CO=OA，以直线AB为对称轴，对ABC作轴对称变换，点C的对应点为E。

P,O,E,D,C,B,A（1，0）,（4）求出点C的坐标，判断点C是否落在（3）中的抛物线上？

F,3.施工工地的水平地面上,有三根外径都是1m的水泥管，两两相切地堆放在一起，则其最高点到地面的距离是,4.三个半径为的圆两两外切，且ABC的每一边都与其中两个圆相切，那么ABC的周长_.,B,A,C,例：

如图已知矩形ABCD的边AB=3厘米，AD=4厘米,

（1）以点A为圆心，3厘米为半径作圆A，则点B、C、D与圆A的位置关系如何？

（B在圆上，D在圆外，C在圆外）,

（2）以点A为圆心，4厘米为半径作圆A，则点B、C、D与圆A的位置关系如何？

（B在圆内，D在圆上，C在圆外）,（3）以点A为圆心，5厘米为半径作圆A，则点B、C、D与圆A的位置关系如何？

（B在圆内，D在圆内，C在圆上）,2cm,3cm,画出由所有到已知点的距离大于或等于2cm并且小于或等于3cm的点组成的图形.,O,思考,例2ABC的内切圆O与BC、CA、AB分别相切于点D、E、F，且AB=9cm，BC=14cm，CA=13cm，求AF、BD、CE的长.,解:

设AF=x（cm）,则AE=x（cm）,CD=CE=AC-AE=13-xBD=BF=AB-AF=9-x,由BD+CD=BC可得（13-x）+（9-x）=14,解得x=4,AF=4（cm）,BD=5（cm）,CE=9（cm）.,记忆:

1.RtABC中,C=90,a=3,b=4,则内切圆的半径是_.,1,4.如图，已知等边三角形ABC中，边长为6cm，求它的外接圆半径。

5.如图，等腰ABC中，求外接圆的半径。

例：

求证：

在一个三角形中，至少有一个内角小于或等于60,已知：

ABC求证：

ABC中至少有一个内角小于或等于60,证明：

假设ABC中没有一个内角小于或等于60，即A60，B60，C60,于是ABC606060180，与三角形的内角和等于180矛盾所以ABC中至少有一个内角小于或等于60。

C,C,B,1、如果扇形的圆心角是20，那么这个扇形的面积等于这个扇形所在圆的面积的_；2、扇形的面积是它所在圆的面积的，这个扇形的圆心角的度数是_；3、扇形的面积是S，它的半径是r，这个扇形的弧长是_.,答案：

240，,小试牛刀,例题讲解,如图23.3.5，圆心角为60的扇形的半径为10厘米，求这个扇形的面积和周长（3.14）,=52.33（平方厘米）；,扇形的周长为,=30.47（厘米）。

解:

因为n60，r10厘米，所以扇形面积为,下面是圆弧形桥拱,其每拱的跨度为40m,拱形的半径为29m,求拱形的高.,转化为数学模型为:

有一圆弧形桥拱,拱的跨度AB=40m,拱形的半径R=29m,求拱形的高.,在直角三角形BOD中:

OD2=OB2-BD2，,解:

如图:

由垂径定理得:

BD=,=20m,OD2=292202，,OD=21m,所以拱形的高CD=29-21=8m,2两圆的半径之比为5:

3，当两圆相切时，圆心距为8cm，求两圆的半径？

解:

设大圆的半径为5x,小圆的半径为3x两圆外切时:

5x+3x=8得x=1两圆半径分别为5cm和3cm,解：

设P的半径为R

（1）若O与P外切，则OP=5+R=8R=3cm,

（2）若O与P内切，则OP=R-5=8，R=13cm所以P的半径为3cm或13cm,.,.,P,O,1.如图O的半径为5cm，点P是O外一点，OP=8cm。

若以P为圆心作P与O相切，求P的半径？

例题,两.圆内切时:

5x-3x=8得x=4两圆半径分别为20cm和12cm,这是一块铁板，上面有A、B、C三个点，经测量，AB=13cm,BC=14cm,CA=9cm,以各顶点为圆心的三个圆两两外切。

求各圆的半径。

答案：

4cm9cm5cm,思考：

圆心A到X轴、Y轴的距离各是多少?

例题1：

.A,O,已知A的直径为6，点A的坐标为（-3，-4），则A与X轴的位置关系是_,A与Y轴的位置关系是_。

B,C,4,3,相离,相切,解：

过C点作CDAB,垂足为D,AB=5,34=5CD,在RtABC中，C=90，AC=3cm，BC=4cm，以C为圆心，r为半径作圆。

想一想?

当r满足_时,C与线段AB只有一个公共点.,r=2.4cm,B,C,A,D,4,5,3,d=2.4cm,或3cmr4cm,三、当堂训练：

1、正方形ABCD的边长为a,以A为圆心，a为半径作圆，则直线BD与A的位置关系是什么？

2、如图,公路MN和PQ在P处交汇,且QPN=30,点A处有一所中学,AP=160米,一拖拉机从点P处沿公路MN行驶，假设拖拉机行使时,周围100米以内会受到噪音的影响,已知拖拉机的速度为18千米时,那么学校会受到影响吗?

如果会,受到影响的时间多长?

例1有一个亭子它的地基是半径为4m的正六边形,求地基的周长和面积（精确到0.1平方米）.,.,O,B,C,r,R,P,3、课堂练习，掌握新知,1、要拧开一个边长为4cm的螺帽，扳手张开的开口b至少要多少？

（5）有若干个等圆外切，正好在围成的空隙中可以作一个同样大小的圆与这若干个圆外切，则这若干个圆的个数是个。

填空题：

6,A,B,O,C,在矩形ABCD中，AB=5，BC=12，如果分别以A、C为圆心的两圆相切，点D在C内，点B在C外，求A的半径r的取值范围。

例1、,如图，在ABC中，BAC90，ABAC，A的半径为1，若点O在BC上运动（与点B、C不重合），设BOx，AOC的面积为y。

（1）求y关于x的函数解析式，写出定义域。

（2）以O为圆心，BO为半径作O与A相切时，求AOC的面积。

例2、,弓形的弦长为6cm，弓形的高为2cm，则这弓形所在的圆的半径为.,3、已知：

如图，O中，AB为弦，C为弧AB的中点，OC交AB于D，AB=6cm，CD=1cm.求O的半径OA.,4.如图,圆O与矩形ABCD交于E、F、G、H,EF=10,HG=6,AH=4.求BE的长.,M,N,已知：

AB和CD是O内的两条平行弦，AB=6cm，CD=8cm，O的半径为5cm，,思考题：

（1）请根据题意画出符合条件的图形,

（2）求出AB、与CD间的距离。

（1）,

（2）,例1：

船能过拱桥吗,.如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗？

相信自己能独立完成解答.,例2：

如图，圆O的弦AB8，DC2，直径CEAB于D，求半径OC的长。

垂径,例3：

如图，已知圆O的直径AB与弦CD相交于G，AECD于E，BFCD于F，且圆O的半径为10，CD=16，求AE-BF的长。

练习3:

如图，CD为圆O的直径，弦AB交CD于E，CEB=30，DE=9，CE=3，求弦AB的长。

挑战自我画一画,3.如图,圆O与矩形ABCD交于E、F、G、H,EF=10,HG=6,AH=4.求BE的长.,垂径定理的应用,例1如图，一条公路的转变处是一段圆弧（即图中弧CD,点O是弧CD的圆心）,其中CD=600m,E为弧CD上的一点,且OECD垂足为F,EF=90m.求这段弯路的半径.,解:

连接OC.,老师提示:

注意闪烁的三角形的特点.,船能过拱桥吗,2.如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗？

相信自己能独立完成解答.,船能过拱桥吗,解:

如图,用表示桥拱,所在圆的圆心为O,半径为Rm,经过圆心O作弦AB的垂线OD,D为垂足,与相交于点C.根据垂径定理,D是AB的中点,C是的中点,CD就是拱高.由题设得,在RtOAD中，由勾股定理，得,解得R3.9（m）.,在RtONH中，由勾股定理，得,此货船能顺利通过这座拱桥.,垂径定理的应用,在直径为650mm的圆柱形油槽内装入一些油后，截面如图所示.若油面宽AB=600mm，求油的最大深度.,垂径定理的逆应用,在直径为650mm的圆柱形油槽内装入一些油后，截面如图所示.若油面宽AB=600mm，求油的最大深度.,D,C,基础训练,1.已知弧长为4cm,它所对的圆心角为120,那么它所对的弦长为（）,2.在O中,所对的圆心角为60,且弦AB=5cm,则的长为（）,C,A,3.如图,在扇形OAB中,AOB=90，已以AB为直径画半圆，则阴影部分面积是（）A.大于SAOBB.等于SAOBC.小于SAOBD.不能确定与SAOB的关系,4.如图,正方形的边长为2,以边长为直径在正方形内画半圆,则阴影部分面积是（）A.-4B.4-C.-2D.4-/4,B,B,5.一个形如圆锥的冰淇淋纸筒，其底面直径为cm,母线长cm,则它的侧面积是（）.66.30.28.15,6.在半径为6cm的圆中，120的圆心角所对的弧长为.,7.扇形半径为12,面积为9,它的圆心角等于度,8.已知扇形的面积为24,弧长为cm,则扇形的半径是cm,圆心角是度,9.已知扇形的面积是12,半径是8cm,则扇形周长是,10.圆锥的底面半径是1cm,母线是2cm,则高是cm,侧面积是，全面积是,D,4cm,22.5,6,240,19,2,3,2、如图,把RtABC的斜边放在直线l上，按顺时针方向在l上转动次，使它转到ABC的位置.设BC=1,AC=求

（1）点A所经过的路线长.

（2）点A所经过的路线与直线l所围成的面积,3、如图,已知扇AOB,AOB=90,OA=OB=4,以OA为直径作半圆M,作MPOB交AB于P,交M于点Q,求阴影部分面积.,4、如图，在中，弦cm,圆周角求阴影部分面积,5、如图：

AB是圆O的直径，弦CD/AB，圆周角CAB等于30度，AB=2cm，求图中阴影部分的面积？

6、如图，矩形ABCD中，AB=1，B