 下学期统计软件在林业中的应用答案.docx
下学期统计软件在林业中的应用答案.docx
- 文档编号:9781719
- 上传时间:2023-02-06
- 格式:DOCX
- 页数:25
- 大小:146.13KB
下学期统计软件在林业中的应用答案.docx
《下学期统计软件在林业中的应用答案.docx》由会员分享,可在线阅读,更多相关《下学期统计软件在林业中的应用答案.docx(25页珍藏版)》请在冰豆网上搜索。
下学期统计软件在林业中的应用答案
统计软件在林业中的应用期末考试试题答案
姓名:
王权龙学号:
201001116012专业:
森林经理学
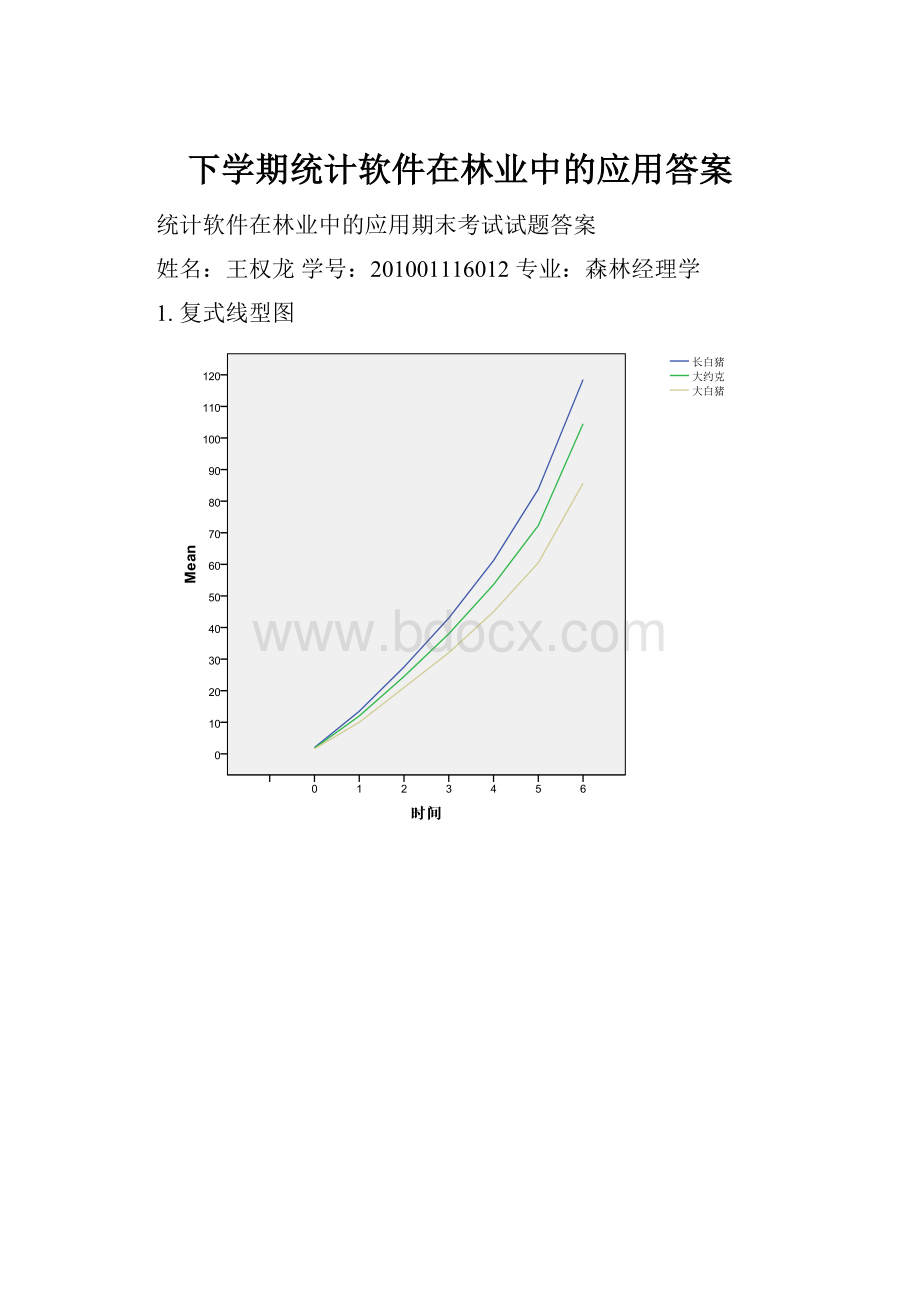
1.复式线型图
复式条型图
2
Descriptives
产鱼量
N
Mean
Std.Deviation
Std.Error
95%ConfidenceIntervalforMean
Minimum
Maximum
LowerBound
UpperBound
a
7
560.00
28.237
10.673
533.89
586.11
530
610
b
6
612.00
23.229
9.483
587.62
636.38
587
642
Total
13
584.00
36.763
10.196
561.78
606.22
530
642
ANOVA
产鱼量
SumofSquares
df
MeanSquare
F
Sig.
BetweenGroups
8736.000
1
8736.000
12.844
.004
WithinGroups
7482.000
11
680.182
Total
16218.000
12
因sig=0.04<0.05说明两种饵料养殖罗非鱼的产鱼量差异性显著.
3
表1.ANOVA
增量
SumofSquares
df
MeanSquare
F
Sig.
BetweenGroups
50.418
4
12.605
6.025
.002
WithinGroups
41.842
20
2.092
Total
92.260
24
由表1可知Sig=0.02<0.05,说明品种间增重有显著差异.
表2.TestofHomogeneityofVariance
增量
LeveneStatistic
df1
df2
Sig.
.363
4
20
.832
表2为方差齐性检验,相伴概率为0.832,远大于显著性水平0.05,表明各品种间增重总体方差相等,可进行多重比较.
表3.MultipleComparisons
DependentVariable:
增量
LSD
(I)品种
(J)品种
MeanDifference(I-J)
Std.Error
Sig.
95%ConfidenceInterval
LowerBound
UpperBound
b1
b2
3.000(*)
.8351
.002
1.258
4.742
b3
1.967(*)
.8758
.036
.140
3.794
b4
.542
.9336
.568
-1.406
2.489
b5
3.792(*)
.9336
.001
1.844
5.739
b2
b1
-3.000(*)
.8351
.002
-4.742
-1.258
b3
-1.033
.8758
.252
-2.860
.794
b4
-2.458(*)
.9336
.016
-4.406
-.511
b5
.792
.9336
.407
-1.156
2.739
b3
b1
-1.967(*)
.8758
.036
-3.794
-.140
b2
1.033
.8758
.252
-.794
2.860
b4
-1.425
.9703
.157
-3.449
.599
b5
1.825
.9703
.075
-.199
3.849
b4
b1
-.542
.9336
.568
-2.489
1.406
b2
2.458(*)
.9336
.016
.511
4.406
b3
1.425
.9703
.157
-.599
3.449
b5
3.250(*)
1.0228
.005
1.117
5.383
b5
b1
-3.792(*)
.9336
.001
-5.739
-1.844
b2
-.792
.9336
.407
-2.739
1.156
b3
-1.825
.9703
.075
-3.849
.199
b4
-3.250(*)
1.0228
.005
-5.383
-1.117
*Themeandifferenceissignificantatthe.05level.
表3为多重性比较,满足方差齐性的LSD法多重比较结果。
根据相伴概率sig与显著性水平的比较,从表中可以看出b1与b2,b3,b5之间差异显著;b2与b1,b4间差异显著;b3与b1,b5之间差异显著;b4与b2,b5差异显著;b5与b2,b3,b4之间差异显著。
4TestsofBetween-SubjectsEffects
DependentVariable:
剂量
Source
TypeIIISumofSquares
df
MeanSquare
F
Sig.
CorrectedModel
13075.000(a)
11
1188.636
.
.
Intercept
100467.000
1
100467.000
.
.
品系
6457.667
3
2152.556
.
.
剂量类别
6074.000
2
3037.000
.
.
品系*剂量类别
543.333
6
90.556
.
.
Error
.000
0
.
Total
113542.000
12
CorrectedTotal
13075.000
11
aRSquared=1.000(AdjustedRSquared=.)
从表中分析知注射不同剂量的雌激素对各品系有显著性差异,说明雌激素的剂量对子宫发育有影响。
5
MultipleComparisons
DependentVariable:
数量
LSD
(I)种类
(J)种类
MeanDifference(I-J)
Std.Error
Sig.
95%ConfidenceInterval
LowerBound
UpperBound
b1
b2
-2.50
2.741
.371
-8.16
3.16
b3
-12.42(*)
2.741
.000
-18.07
-6.76
b2
b1
2.50
2.741
.371
-3.16
8.16
b3
-9.92(*)
2.741
.001
-15.57
-4.26
b3
b1
12.42(*)
2.741
.000
6.76
18.07
b2
9.92(*)
2.741
.001
4.26
15.57
Basedonobservedmeans.
Themeandifferenceissignificantatthe.05level.
从表可以看出,b3与其他两种差异最显著,属于最优。
MultipleComparisons
DependentVariable:
数量
LSD
(I)肥源
(J)肥源
MeanDifference(I-J)
Std.Error
Sig.
95%ConfidenceInterval
LowerBound
UpperBound
a1
a2
17.67(*)
3.165
.000
11.13
24.20
a3
13.44(*)
3.165
.000
6.91
19.98
a4
3.67
3.165
.258
-2.87
10.20
a2
a1
-17.67(*)
3.165
.000
-24.20
-11.13
a3
-4.22
3.165
.195
-10.75
2.31
a4
-14.00(*)
3.165
.000
-20.53
-7.47
a3
a1
-13.44(*)
3.165
.000
-19.98
-6.91
a2
4.22
3.165
.195
-2.31
10.75
a4
-9.78(*)
3.165
.005
-16.31
-3.25
a4
a1
-3.67
3.165
.258
-10.20
2.87
a2
14.00(*)
3.165
.000
7.47
20.53
a3
9.78(*)
3.165
.005
3.25
16.31
Basedonobservedmeans.
*Themeandifferenceissignificantatthe.05level.
从表可以看出,a1与其他几种差异最显著,属于最优。
6做理想的回归方程
表1:
偏回归系数方差分析
ANOVAb
Model
SumofSquares
df
MeanSquare
F
Sig.
1
Regression
1.382E7
5
2763775.354
1128.303
.000a
Residual
24494.981
10
2449.498
Total
1.384E7
15
a.Predictors:
(Constant),x5,x3,x4,x2,x1
b.DependentVariable:
y
由表可见,F=1128.303,P≈0<0.01,表明y—民航客运量与x1—国民收入(亿元)、x2—消费额(亿元)、x3—铁路客运量(万人)、x4—民航航线里程(万公里)、x5—来华旅游入境人数(万人)的综合线性影响是极显著的。
表2:
各变量偏回归系数及其检验
Coefficientsa
Model
UnstandardizedCoefficients
StandardizedCoefficients
t
Sig.
B
Std.Error
Beta
1
(Constant)
450.909
178.078
2.532
.030
x1
.354
.085
2.447
4.152
.002
x2
-.561
.125
-2.485
-4.478
.001
x3
-.007
.002
-.083
-3.510
.006
x4
21.578
4.030
.531
5.354
.000
x5
.435
.052
.564
8.440
.000
a.DependentVariable:
y
根据上表课建立以下多元回归方程:
Y=450.909+0.354x1-0.561x2-0.007x3+21.578x4+0.435x5。
并从表中得,偏回归系数x1—国民收入(亿元)、x2—消费额(亿元)、x3—铁路客运量(万人)、x4—民航航线里程(万公里)、x5—来华旅游入境人数(万人)相应的t值和显著性概率分别为tx1=4.152,px1=0.030<0.05;tx2=-4.478,px2=0.002<0.01;tx3=-3.510,px3=0.006<0.01;tx4=5.354,px4=0.000<0.01;tx5=8.440,px5=0.000<0.01所有的偏回归系数都显著说明该回归方程是最优方程。
7.聚类分析如下:
表1:
中国房地产9个指标间的相关系数阵
ProximityMatrix
Case
MatrixFileInput
x1
x2
x3
x4
x5
x6
x7
x8
x9
x1
.000
1470654.000
3.009E8
1.927E8
2.123E8
1.701E8
8.137E7
2.715E8
2.888E8
x2
1470654.000
.000
3.351E8
1.680E8
2.403E8
1.980E8
7.412E7
2.468E8
2.617E8
x3
3.009E8
3.351E8
.000
8.906E8
1.366E8
1.319E8
5.212E8
9.349E8
9.931E8
x4
1.927E8
1.680E8
8.906E8
.000
7.054E8
5.883E8
1.002E8
7.657E7
6.376E7
x5
2.123E8
2.403E8
1.366E8
7.054E8
.000
1.056E8
4.088E8
7.674E8
8.162E8
x6
1.701E8
1.980E8
1.319E8
5.883E8
1.056E8
.000
3.174E8
6.561E8
7.011E8
x7
8.137E7
7.412E7
5.212E8
1.002E8
4.088E8
3.174E8
.000
1.812E8
1.846E8
x8
2.715E8
2.468E8
9.349E8
7.657E7
7.674E8
6.561E8
1.812E8
.000
2418251.435
x9
2.888E8
2.617E8
9.931E8
6.376E7
8.162E8
7.011E8
1.846E8
2418251.435
.000
表2:
聚类过程描述表
AgglomerationSchedule
Stage
ClusterCombined
Coefficients
StageClusterFirstAppears
NextStage
Cluster1
Cluster2
Cluster1
Cluster2
1
1
2
1470654.000
0
0
4
2
8
9
2418251.435
0
0
3
3
4
8
7.017E7
0
2
7
4
1
7
7.775E7
1
0
7
5
5
6
1.056E8
0
0
6
6
3
5
1.343E8
0
5
8
7
1
4
2.106E8
4
3
8
8
1
3
5.421E8
7
6
0
从以上两表可分析如下:
由于该过程有9个变量,因此需经过9步聚类。
第一步:
变量x1与变量x2聚成一类,凝聚系数为1470654.000,与相关系数1470654.000一致。
第二步:
变量x8与变量x9聚成一类,凝聚系数为2418251.435,该凝集系数和变量x8和x9的相关系数一致,因为变量x8和x9事先都没有进入任何一组。
第三步:
变量x4与变量x8聚成一类,即变量x4进入已聚类的“变量x8与变量x9”之中,其凝聚系数为7.017E7,它不等于变量x4与变量x8的相关系数7.657E7。
也不等于变量x4与变量x9的相关系数6.376E7。
因此此处的凝聚系数是变量x4与变量x8、变量x9联合成后多重相关系数。
第四步:
变量x1与变量x7聚成一类,即变量x7进入已聚类的“变量x1与变量x2”之中,其凝聚系数为7.775E7,它不等于变量x7与变量x1的相关系数8.137E7,也不等于变量x7与变量x2的相关系数7.412E7。
因此此处的凝聚系数是变量x7与变量x1、变量x2联合成后多重相关系数。
第五步:
变量x5与变量x6聚成一类,凝聚系数为1.056E8,该凝集系数和变量x5和x6的相关系数一致,因为变量x5和x6事先都没有进入任何一组。
第六步:
变量x3与变量x5聚成一类,即变量x3进入已聚类的“变量x5与变量x6”之中,其凝聚系数为1.343E8,它不等于变量x3与变量x5的相关系数1.366E8,也不等于变量x3与变量x6的相关系数1.319E8。
因此此处的凝聚系数是变量x3与变量x5、变量x6联合成后多重相关系数。
第七步:
变量x1与变量x4聚成一类,即变量x4进入已聚类的“变量x1与变量x2”之中,其凝聚系数为2.106E8,它不等于变量x4与变量x1的相关系数1.927E8,也不等于变量x4与变量x2的相关系数1.680E8。
因此此处的凝聚系数是变量x4与变量x1、变量x2联合成后多重相关系数。
第八步:
变量x1与变量x3聚成一类,即变量x3进入已聚类的“变量x1与变量x2”之中,其凝聚系数为5.421E8,它不等于变量x3与变量x1的相关系数3.009E8,也不等于变量x3与变量x2的相关系数3.351E8。
因此此处的凝聚系数是变量x3与变量x1、变量x2联合成后多重相关系数。
8.建立判别函数,并判定另外4个待判样品属于哪类?
根据SPSS判别分析可得以下数据:
表1:
Eigenvalues
Function
Eigenvalue
%ofVariance
Cumulative%
CanonicalCorrelation
1
59.330(a)
98.8
98.8
.992
2
.693(a)
1.2
100.0
.640
aFirst2canonicaldiscriminantfunctionswereusedintheanalysis.
表2:
Wilks'Lambda
TestofFunction(s)
Wilks'Lambda
Chi-square
df
Sig.
1through2
.010
43.948
12
.000
2
.591
4.999
5
.416
表3:
StandardizedCanonicalDiscriminantFunctionCoefficients
Function
1
2
X1
-17.046
-7.677
X2
14.757
9.870
X3
-1.306
-.513
X4
6.381
-.666
X5
1.332
.710
X6
4.315
1.833
表4:
CanonicalDiscriminantFunctionCoefficients
Function
1
2
X1
-1.950
-.878
X2
1.748
1.169
X3
-.930
-.365
X4
.825
-.086
X5
.102
.054
X6
1.662
.706
(Constant)
-78.896
-30.330
表5:
FunctionsatGroupCentroids
类型
Function
1
2
第一组
-2.647
1.013
第二组
9.444
-.259
第三组
-6.797
-.754
表6:
ClassificationFunctionCoefficients
类型
第一组
第二组
第三组
X1
-159.015
-181.479
-149.370
X2
168.068
187.715
158.749
X3
-98.413
-109.195
-93.908
X4
58.217
68.296
54.948
X5
11.702
12.862
11.185
X6
202.770
221.972
194.625
(Constant)
-5628.382
-6584.377
-5266.780
表7:
CasewiseStatistics
CaseNumber
ActualGroup
HighestGroup
DiscriminantScores
PredictedGroup
P(D>d|G=g)
P(G=g|D=d)
SquaredMahalanobisDistancetoCentroid
Function1
Function2
p
df
1
1
1
.846
2
1.000
.334
-2.197
1.375
2
1
1
.876
2
1.000
.266
-2.292
1.386
3
1
1
.942
2
1.000
.119
-2.782
1.330
4
1
1
.756
2
.999
.561
-3.289
.628
5
1
1
.800
2
1.000
.445
-2.677
.346
6
2
2
.789
2
1.000
.474
9.939
.219
7
2
2
.659
2
1.000
.835
8.594
-.594
8
2
2
.050
2
1.000
5.990
10.332
-2.540
9
2
2
.091
2
1.000
4.786
8.627
1.771
10
2
2
.955
2
1.000
.092
9.728
-.151
11
3
3
.936
2
1.000
.132
-6.901
-.406
12
3
3
.836
2
1.000
.359
-7.393
-.693
13
3
3
.076
2
1.000
5.152
-8.834
-1.756
14
3
3
.178
2
.905
3.457
-4.942
-.630
15
3
3
.607
2
.997
.998
-5.914
-.286
16
ungrouped
3
.000
2
1.000
395.903
-21.903
-13.704
17
ungrouped
1
.745
2
.999
.588
-3.393
.834
18
ungrouped
2
.000
2
1.000
31.237
14.502
2.120
19
ungrouped
3
.310
2
1.000
2.344
-7.914
-1.801
表8:
ClassificationResults(a)
类型
Predi
- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 下学 统计 软件 林业 中的 应用 答案
 冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。


 《城市规划基本知识》深刻复习要点.docx
《城市规划基本知识》深刻复习要点.docx
