多边形综合练习.docx

多边形综合练习.docx

《多边形综合练习.docx》由会员分享，可在线阅读，更多相关《多边形综合练习.docx（18页珍藏版）》请在冰豆网上搜索。

多边形综合练习

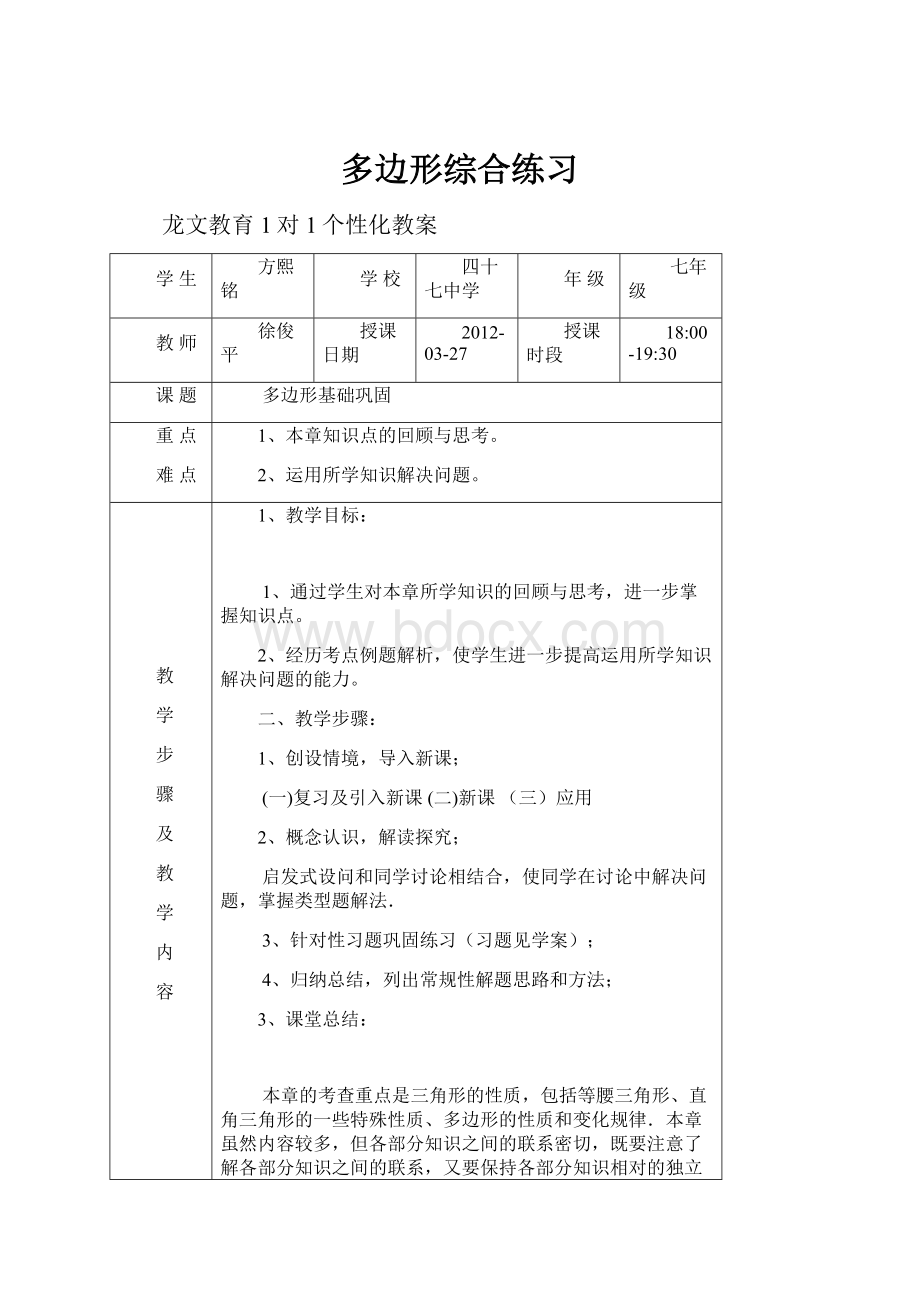
龙文教育1对1个性化教案

学生

方熙铭

学校

四十七中学

年级

七年级

教师

徐俊平

授课日期

2012-03-27

授课时段

18:

00-19:

30

课题

多边形基础巩固

重点

难点

1、本章知识点的回顾与思考。

2、运用所学知识解决问题。

教

学

步

骤

及

教

学

内

容

1、教学目标：

1、通过学生对本章所学知识的回顾与思考，进一步掌握知识点。

2、经历考点例题解析，使学生进一步提高运用所学知识解决问题的能力。

二、教学步骤：

1、创设情境，导入新课；

（一）复习及引入新课

（二）新课（三）应用

2、概念认识，解读探究；

启发式设问和同学讨论相结合，使同学在讨论中解决问题，掌握类型题解法．

3、针对性习题巩固练习（习题见学案）；

4、归纳总结，列出常规性解题思路和方法；

3、课堂总结：

本章的考查重点是三角形的性质，包括等腰三角形、直角三角形的一些特殊性质、多边形的性质和变化规律．本章虽然内容较多，但各部分知识之间的联系密切，既要注意了解各部分知识之间的联系，又要保持各部分知识相对的独立性．本章的难点是推理入门．以前在第一册中已了解了推理证明，以及证明几何命题的一般方法步骤，是为现在正规练习证明做准备的．证明要求掌握有理有据地推理，精练准确地表达过程，有一定难度．

四、课后作业：

（见学案）

教导处签字：

日期：

年月日

课后

评价

一、学生对于本次课的评价

O特别满意O满意O一般O差

二、教师评定

1、学生上次作业评价

O好O较好O一般O差

2、学生本次上课情况评价

O好O较好O一般O差

作业

布置

教师

留言

教师签字：

家长

意见

家长签字：

日期：

年月日

教学讲义

教学目标：

1、通过学生对本章所学知识的回顾与思考，进一步掌握知识点；

2、经历考点例题解析，使学生进一步提高运用所学知识解决问题的能力。

教学重点：

本章知识点的回顾与思考。

教学难点：

运用所学知识解决问题。

教学步骤：

典型例题：

例1、一个多边形，它的外角最多有几个是钝角？

说说你的理由．

例2、一个五边形截去一个角后就一定是三角形吗？

画出所有可能的图形，并分别说出内角和和外角和变

化情况．

例3、一个n边形除了一个内角之外，其余各内角之和是1780度求这个多边形的边数n和这个内角的度数？

1、

（1）六边形的内角和是，外角和是．

（2）一个多边形的内角和与外角和都是360°，这个多边形是边形．

（3）一个十边形所有内角都相等，它的每一个外角等于度．

（4）多边形边数增加一条，则它的内角和增加度，外角和．

（5）一个多边形的每一个外角都是72°，那么这个多边形的内角和为．

2、一个多边形每一个外角都等于与它相邻的内角，这种多边形是几边形能确定它的每一个外角的度数吗？

3、任意多边形的外角和等于__________．

课堂精练：

1、一个多边形，它的内角和是外角和的2倍，这个多边形的边数是（）．

A．3B．4C．5D．6

2、一个多边形，它的每个内角都等于相邻外角的5倍，则这个多边形是（）

A．正五边形B．正十边形C．正十二边形D．不存在．

3、n边形所有对角线的条数是（）

A.

B.

C.

D.

4.如果多边形的内角和是外角和的k倍，那么这个多边形的边数是（）

A.kB.2k+1C.2k+2D.2k-2

5.若把一个多边形的顶点数增加一倍，它的内角和是25200，那么原多边形的顶点数为（）

A.8B.9C.6D.10

6.若一个多边形的边数增加１，则它的内角和（　）

Ａ.不变　　　Ｂ.增加１　　Ｃ.增加180°　　　Ｄ.增加360°

7.当一个多边形的边数增加时，其外角和（　　）

Ａ.增加　　　Ｂ.减少　　Ｃ.不变　　　Ｄ.不能确定

8.某学生在计算四个多边形的内角和时，得到下列四个答案，其中错误的是（　　）

A.180°B.540°C.1900°D.1080°

9.如果一个多边形的内角和是720°，那么这个多边形的对角线的条数是（　　）

Ａ.6Ｂ.9Ｃ.14Ｄ.20

10.如果一个多边形的内角和是它的外角和的n倍，则这个多边形的边数是（　　）

Ａ.n　　Ｂ.2n-2　Ｃ.2n　Ｄ.2n+2

11.一个多边形截去一个角（不过顶点）后，形成的多边形的内角和是2520°那么原多边形的边数是（　　）

Ａ.13　　　Ｂ.14　　Ｃ.15　　Ｄ.13或15

12.一个多边形的内角和是它的外角和的4倍，这个多边形是（　　）

Ａ.四边形　　Ｂ.六边形　　　Ｃ.八边形　　Ｄ.十边形

13.一个多边形中，除一个内角外，其余各内角和是120°，则这个角的度数是（　）

Ａ.60°　　Ｂ.80°　　Ｃ.100°　Ｄ.120°

14.用下列一种正多边形可以拼地板的是（）

A.正五边形B.正六边形C.正八边形D.正十二边形

15.多边形每一个内角都等于120°,则从此多边形一个顶点出发可引的对角线的条数是（）

A.5条B.4条C.3D.2条

16.若一个多边形除了一个内角外,其余各内角之和是2570°,则这个角是（）

A.90°B.15°C.120°D.130°

17.在多边形的内角中,锐角的个数不能多于（）

A.2个B.3个C.4个D.5个

18.n边形的边数增加一倍,它的内角和增加（）

A.180°B.360°C.（n-2）.180°D.n.180°

19、一个多边形的外角中,钝角的个数不可能是（）毛

A.1个B.2个C.3个D.4个

20.若一个多边形的各内角都相等,则一个内角与一个外角的度数之比不可能是（）

A.2:

1B.1:

1C.5:

2D.5:

4

21.一个多边形的内角中,锐角的个数最多有（）

A.3个B.4个C.5个D.6个

22.四边形中,如果有一组对角都是直角,那么另一组对角可能（）

A.都是钝角;B.都是锐角C.是一个锐角、一个钝角D.是一个锐角、一个直角

23.若从一个多边形的一个顶点出发,最多可以引10条对角线,则它是（）

A.十三边形B.十二边形C.十一边形D.十边形

24.若一个多边形共有十四条对角线,则它是（）

A.六边形B.七边形C.八边形D.九边形

25、若一个多边形除了一个内角外,其余各内角之和为2570°,则这个内角的度数为（）

A.90°B.105°C.130°D.120°

26.用形状、大小完全相同的图形不能镶嵌成平面图案的是（）毛

A.等腰三角形B.正方形C.正五边形D.正六边形

27.下列图形中,能镶嵌成平面图案的是（）

A.正六边形B.正七边形C.正八边形D.正九边形

28.不能镶嵌成平面图案的正多边形组合为（）

A.正八边形和正方形B.正五边形和正十边形

C.正六边形和正三角形D.正六边形和正八边形

29.如图所示,各边相等的五边形ABCDE中,若∠ABC=2∠DBE,则∠ABC等于（）

A.60°B.120°C.90°D.45°

填空题精练：

1.用正三角形和正六边形镶嵌,在每个顶点处有_______个正三角形和_____个正六边形,或在每个顶点处有______个正三角形和________个正六边形.

2.用正多边形镶嵌,设在一个顶点周围有m个正方形、n个正八边形,则m=_____,n=______.

3.用一种正五边形或正八边形的瓷砖_______铺满地面.（填“能”或“不能”）

4.一个多边形的内角和与外角和相等，则这个多边形是边形.

5.多边形的边数增加一条时，其外角和，内角和增加.

6.一个多边形的内角和是外角和的5倍,那么这个多边形的边数是.

7.从n边形的一个顶点出发,最多可以引______条对角线,这些对角线可以将这个多边形分成__个三角形.

8.如果一个多边形的每一个内角都相等,且每一个内角都大于135°,那么这个多边形的边数最少为___.

9.已知一个多边形的每一个外角都相等,一个内角与一个外角的度数之比为9:

2,则这个多边形的边数为_.

10.每个内角都为144°的多边形为_________边形.

11.如果一个多边形的内角和等于1800°，则这个多边形是___边形；如果一个ｎ边形每一个内角都是

135°，则＝ｎ___；

12、如果一个ｎ边形每一个外角都是36°，则＝ｎ______。

13.如果一个多边形的内角和等于900°,那么这个多边形是_____边形.

14.一个正多边形的每个外角都等于30°,则这个多边形边数是______.

15.n边形的外角和与内角和的度数之比为2:

7,则边数为_______.

16.从一个多边形的一个顶点出发,一共做了10条对角线,则这个多边形的内角和为_____度.

17.在四边形ABCD中,如果∠A:

∠B:

∠C:

∠D=1:

2:

3:

4,则∠D=______.

18.用正方形和正十二边形以及正_____边形可以拼地板.

19.n边形的内角和等于______度。

任意多边形的外角和等于______度。

20.如果十边形的每个内角都相等，那么它的每个内角都等于______度，每个外角都等于______度。

21.若多边形的内角和是1080°，则这个多边形是______边形。

22．一个n边形的每一个外角都等于72°，则n=，它的内角和是。

23．

（1）n边形的内角和等于，多边形的外角和都等于．

（2）一个多边形的内角和等于它的外角和，那么这个多边形是边形．

（3）一个多边形的每个外角都是300，则这个多边形是边形．

（4）一个十边形所有内角都相等，它的每一个外角等于度．

（5）一个五边形五个外角的比是2：

3：

4：

5：

6，则这个五边形五个外角的度数分别是．

（6）多边形边数增加一条，则它的内角和增加度，外角和．

24.n边形的内角和=________度，外角和=_______度。

25.如果一个多边形的内角和与它的外角和相等，那么这个多边形是____边形。

26.如果一个多边形的内角和等于它的外角和5倍，那么这个多边形是____边形。

27.若n边形的每个内角都是150°，则n=____。

28.一个多边形的每个外角都是36°，这个多边形是______边形。

29.如果一个多边形的每个内角都相等，且内角的度数是与它相邻的外角度数的2倍，那么这个边形的每

个内角是_____度，其内角和等于______度。

30、若一个多边形的内角和是1800°，则这个多边形的边数是_______。

解答题精讲：

1.若两个多边形的边数之比为1：

2，两个多边形的内角和之和为1440°，求这两个多边形的边数。

2．一个多边形的外角和是内角和的

，它是几边形？

3．一个多边形的每一个外角都是72°，那么这个多边形的内角和为多少度？

4．一个多边形每一个外角都等于与它相邻的内角，这种多边形是几边形能确定它的每一个外角的度数吗？

5、一个多边形的各个内角都相等，且一个内角是150°，你知道它是几边形吗？

6.一个多边形的每一个外角都等于24°,求这个多边形的边数.

7．一个零件的形状如图中阴影部分．按规定∠A应等于90º，∠B、∠C应分别是29º和21º，检验人员度

量得∠BDC＝141º，就断定这个零件不合格．你能说明理由吗？

8．若两个多边形的边数相差1，则它们的内角和、外角和分别有什么异同？

9．一个多边形，它的外角最多有几个是钝角？

说说你的理由．

10．一个四边形截去一个角后就一定是三角形吗？

画出所有可能的图形，并分别说出内角和和外角和变化

情况．

11．如图，求∠A＋∠B＋∠C＋∠D＋∠E＋∠F度数。

12．一个多边形除了一个内角外，其余各内角的和为2478°求这个内角的度数。

13.求图15-13①、②中，∠A+∠B+∠C+∠D+∠E的度数。

14.一个五边形的五个外角的读数比是1∶2∶3∶4∶5，求这个五边形的五个内角的度数比.

15.两个正多边形的边数之比为1∶2，内角和之比为3∶8，求这两个多边形的边数、内角和

16.一个多边形出一个内角外，其余个内角的和为20300，求这个多边形的边数.

课后练习：

1、三角形的一个外角等于与它不相邻的；

2、三角形的一个外角大于任何一个与它.

3、已知一个多边形的内角和是2340度，这个多边形是　　　边形。

4、等腰三角形两条边长为25、12，则其周长为　　　　

5、如果一个三角形的3个外角的度数之比是2:

3:

4，则其相邻内角的度数比为　　　

6、用多种正多边形拼地板，关键是看这几个正多边形的内角加起来要等于　　　　

7、正十边形的每一个内角的度数等于　　　

8、如图，AC⊥BD于C，已知∠A＝40°，∠AEF＝70°，∠D＝　　　　

（第8题图）

9.4条线段的长度分别为2，3,　4，5，任选3条线段可以组成　　个三角形。

10、用正三角形和正四边形作平面镶嵌，在一个顶点周围，可以有　　　个在三角形和　　个正四边形。

11、已知等腰三角形的一边长等于5，一边长等于6，则它的周长为______.

12、三角形三个角的比为3：

2：

5，则三个角分别为______.

13、在

ABC中，若

B+

A=2

C，则

C=_____.。

14、在

ABC中，若

C+

A=2

B，

C-

A=

，则

A=_____,

B=_____,

C=_____.

15、在三角形中，相邻的外角是内角的2倍，则这两个角的度数为______.

16、在△ABC中，∠A＋∠B=∠C，则△ABC是三角形。

17、从一个多边形的一个顶点出发，作了15条对角线，则这个多边形的内角和为。

18、在△ABC中，AB＝AC，∠A＝36度，CD平分∠ACB，则图中的等腰三角形有个。

分别

是。

19、已知：

如图，五角星中，∠A＋∠B＋∠C＋∠D＋∠E＝＿＿＿。

20、多边形每增加一条边，那么它的内角和增加＿＿，外角和＿＿＿。

21、多边形的内角中，最多有＿＿＿＿个锐角。

二、选择：

1、下列的线段哪些可以组成三角形（　　　）

A、10，14，24　B、12，2，16，　C、16，6，4　D、8，10，12

2、等腰三角形的一个外角等于100度，这个等腰三角形的底角的度数为（）

A、45度B、50度C、80度或50度D、45度或50度

3、已知等腰三角形的周长为24，一边长为4，则另一边长是（）

A、10B、16C、10或16D、无法确定

4、一个三角形的两边长分别是3和8，而第三边长为奇数，那么第三边长是（）

A、5或7B、7或9C、9或11D、11

5、不能够铺满地面的组合图形是（）

A、正八边形和正方形B、正方形和正三角形

C、正六边形和正方形D、正六边形和正三角形

6、一个多边形的内角和比它的外角和的3倍少

，这个多边形的边数是（）

A、5条B、6条C、7条D、8条

7、小明不慎将一块三角形的玻璃摔碎成如图所示的四块（即图中标有1、2、3、4的四块），你认为将其中的哪一块带去，就能配一块与原来一样大小的三角形?

应该带＿＿＿＿。

A．第1块B．第2块C．第3块D．第4块

8、

ABC中，三边长为6，7，

，则

的取值范围是（）

A、

B、

C、

D、无法确定

9、把三角形的面积分为相等的两部分的是（　　　　）

A.三角形的角平分线　B、三角形的中线　C、三角形的高　D、以上都不对

10、适合条件

的三角形是（）

A、锐角三角形B、直角三角形C、钝角三角形D、不能确定

11、如果三角形的一个外角小于和它相邻的内角，那么这个三角形为（）

A、钝角三角形B、锐角三角形C、直角三角形D、斜三角形

12、若ΔABC边为a、b、c，则|a－b－c|＋|b－c－a|＋|c－a－b|＝（）。

A、－a－b－c　B、a＋b＋cC、a＋b－c　D、a－b＋c

13、若一个多边形的边数增加2倍，它的外角和（　　　　）

A.扩大2倍　B、缩小2倍　C、保持不变　D、无法确定

14、具备下列条件的三角形中，不为直角三角形的是（　　　）

A、∠A＋∠B＝∠C　　　　　　　　B、∠A＝∠B＝∠C/2

C、∠A＝90°－∠B　　　　　　　D、∠A－∠B＝90°

15、一个多边形的内角和比它的外角和的2倍还大180°，这个多边形的边数是（　）

A、5　　　　　B、6　　　　　C、7　　　　　D、8

三、1.作图：

分别作出下列三角形的三条高：

2、按图中所给的条件，求出∠1、∠2、∠3的度数.

3、如图，飞机要从A地飞往B地，因受大风影响，一开始就偏离航线（AB）18°（即∠A＝18°）飞到了C地，经B地的导航站测得∠ABC＝10°.此时飞机必须沿某一方向飞行才能到达能到达B处.那么这一方向与水平方向的夹角∠BCD的度数？

4、如图：

∠A＝70度，若O为两条角平分线的交点，求∠BOC的度数。

5、如图：

在△ABC中，∠ABC和∠ACB平分线交于点O，过点O作EF∥BC，交AB于E，交AC于F，且△

ABC的周长是24cm，BC＝10cm，求△AEF的周长?

6、如图，在

ABC中，BD是

ABC的角平分线，DE//BC，交AB于E，∠A=450,∠BDC=600，求ΔBDE各内

角的度数．

7、一个多边形每个内角相等，并且每一个外角等于一个内角的

，求此多边形的边数。

8、如图，已知DC是△ABC中∠ACB的外角平分线，说明为什么∠BAC＞∠B.