小升初几何之等积蝴蝶鸟头.docx

小升初几何之等积蝴蝶鸟头.docx

《小升初几何之等积蝴蝶鸟头.docx》由会员分享，可在线阅读，更多相关《小升初几何之等积蝴蝶鸟头.docx（12页珍藏版）》请在冰豆网上搜索。

小升初几何之等积蝴蝶鸟头

小升初几何重点复习

——等积、蝴蝶、鸟头

小升初考试中几何题目一般都较难，而三角形中常见的三大几何模型——等积模型，蝶形模型，鸟头模型就是三角形计算的重要部分，近几年成都各大名校的选拔考试的面积题目，也有逐步增加难度的趋势。

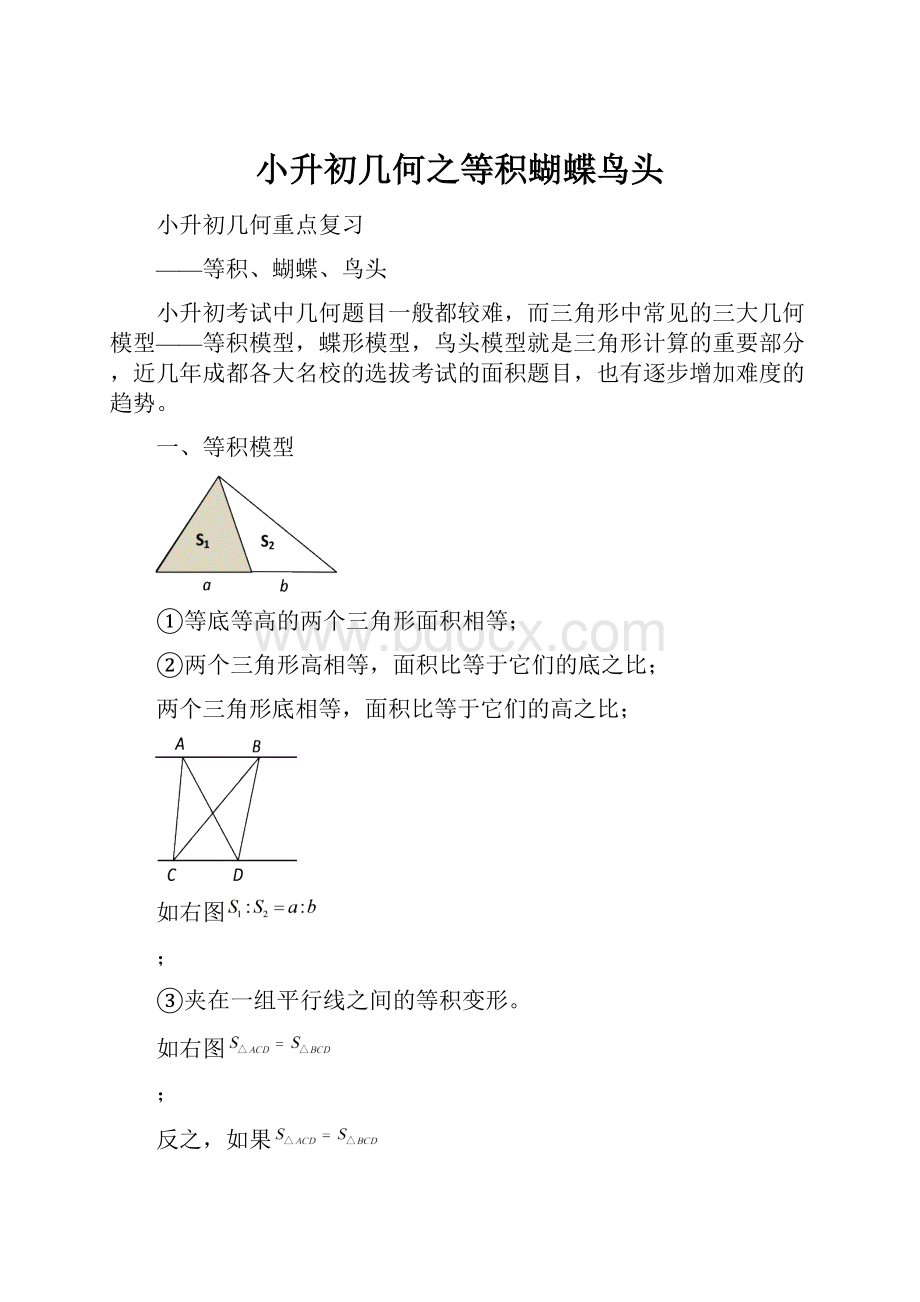
一、等积模型

①等底等高的两个三角形面积相等；

②两个三角形高相等，面积比等于它们的底之比；

两个三角形底相等，面积比等于它们的高之比；

如右图

；

③夹在一组平行线之间的等积变形。

如右图

；

反之，如果

，则可知直线AB平行于CD；

④等底等高的两个平行四边形面积相等（长方形和正方形可以看作特殊的平行四边形）；

⑤三角形面积等于与它等底等高的平行四边形面积的一半；

⑥两个平行四边形高相等，面积比等于它们的底之比；两个平行四边形底相等，面积比等于它们的高之比。

二、蝴蝶模型

任意四边形中的比例关系（“蝶形定理”）：

①

或者

②

蝴蝶模型为我们提供了解决不规则四边形的面积问题的一个途径。

通过构造模型，一方面可以使不规则四边形的面积关系与四边形内的三角形相联系；另一方面，也可以得到与面积对应的对角线的比例关系。

特别的，在梯形中比例关系（“梯形蝶形定理”）：

①

；

②

；

③

的对应份数为

。

【例1】如图，有大小两个正方形ABCD和CEFG，其中正方形CEFG的边长为2，求阴影部分的面积。

1、三个正方形ABCD，BEFG，HKPF如图所示放置在一起，图中正方形BEFG的周长等于14厘米。

求图中阴影部分的面积。

【例2】如图，正方形ABCD的边长为6，AE＝1.5，CF＝2。

求长方形EFGH的面积。

2、如图所示，正方形ABCD的边长为8厘米，长方形EBGF的长BG为10厘米，那么长方形的宽为几厘米？

【例3】长方形ABCD的面积为36cm2，E、F、G为各边中点，H为AD边上任意一点，问阴影部分面积是多少？

3、如图，已知长方形ADEF的面积是16，三角形ADB的面积是3，三角形ACF的面积是4，那么三角形ABC的面积是多少？

【例4】如图，在梯形ABCD中，AD：

BE=4：

3，BE：

EC=2：

3，且△BOE的面积比△AOD的面积小10平方厘米。

梯形ABCD的面积是多少平方厘米？

4、已知ABCD是平行四边形，BC：

CE=3：

2，三角形ODE的面积为6平方厘米，则阴影部分的面积是多少平方厘米？

【例5】如图，正方形ABCD面积为

平方厘米，M是AD边上的中点，求图中阴影部分的面积。

5、如图，长方形ABCD被CE、DF分成四块，已知其中3块的面积分别为2、5、8平方厘米，那么余下的四边形OFBC的面积为多少平方厘米？

巩固练习

1、如图，四边形被两条对角线分成4个三角形，其中三个三角形的面积已知，求：

（1）三角形BGC的面积；

（2）AG：

GC的值

2、如图，某公园的外轮廓是四边形ABCD，被对角线AC、BD分成四个部分，△AOB面积为1平方千米，△BOC面积为2平方千米，△COD的面积为3平方千米，公园陆地的面积是6.92平方千米，求人工湖的面积是多少平方千米？

3、如图所示，BD、CF将长方形ABCD分成4块，△DEF的面积是4cm2，△CED的面积是6cm2。

问：

四边形ABEF的面积是多少平方厘米？

v4、如图所示，长方形ABCD内的阴影部分的面积之和为70，AB＝8，AD＝15，四边形EFGO的面积为。

三、鸟头模型

两个三角形中有一个角重合或互补，这两个三角形叫做共角三角形。

共角三角形的面积比等于对应角（重合角或互补角）两夹边的乘积之比。

如下图在

中，

分别是直线AB、AC上的点（或D在BA的延长线上，E在AC上），则

【例1】如图，CD＝2BC，AE＝2AC，△ABC的面积为1cm2，求△CDE的面积。

1、如图，在△ABC中，D在BA的延长线上，E在AC上，且AB:

AD＝5:

2，AE:

EC＝3:

2，△ADE是12平方厘米，求△ABC的面积。

【例2】如图，在△ABC中，BD＝DC＝4，BE＝3，AE＝6，求乙是甲面积的几倍？

【例3】如右图，将三角形ABC的BA边延长1倍到D，CB边延长2倍到E，AC边延长3倍到F。

如果三角形ABC的面积等于l，则三角形DEF的面积=。

【例4】如右图，平行四边形ABCD，BE＝AB，CF＝2CB，GD＝3DC，HA＝4AD，平行四边形ABCD的面积是2，求平行四边形ABCD与四边形EFGH的面积比。

【例5】已知△DEF的面积为7平方厘米，BE＝CE，AD＝2BD，CF＝3AF，求△ABC的面积。

巩固练习

1、如图，△ABC中，AB是AD的5倍，AC是AE的3倍，如果△ADE的面积等于1，那么△ABC的面积是多少？

2、已知△ABC面积为1，延长AB至D，使BD＝AB；延长BC至E，使CE＝BC；延长CA至F，使AF＝AC，求△DEF的面积。

3

、如右图BE＝

BC，CD＝

AC，那么三角形AED的面积是三角形ABC面积的______。

4、如图，四边形EFGH的面积是66平方米，EA＝AB，CB＝BF，DC＝CG，HD＝DA，四边形ABCD的面积。