自动控制原理胡寿松第5版课后习题及答案完整.docx

自动控制原理胡寿松第5版课后习题及答案完整.docx

《自动控制原理胡寿松第5版课后习题及答案完整.docx》由会员分享，可在线阅读，更多相关《自动控制原理胡寿松第5版课后习题及答案完整.docx（274页珍藏版）》请在冰豆网上搜索。

自动控制原理胡寿松第5版课后习题及答案完整

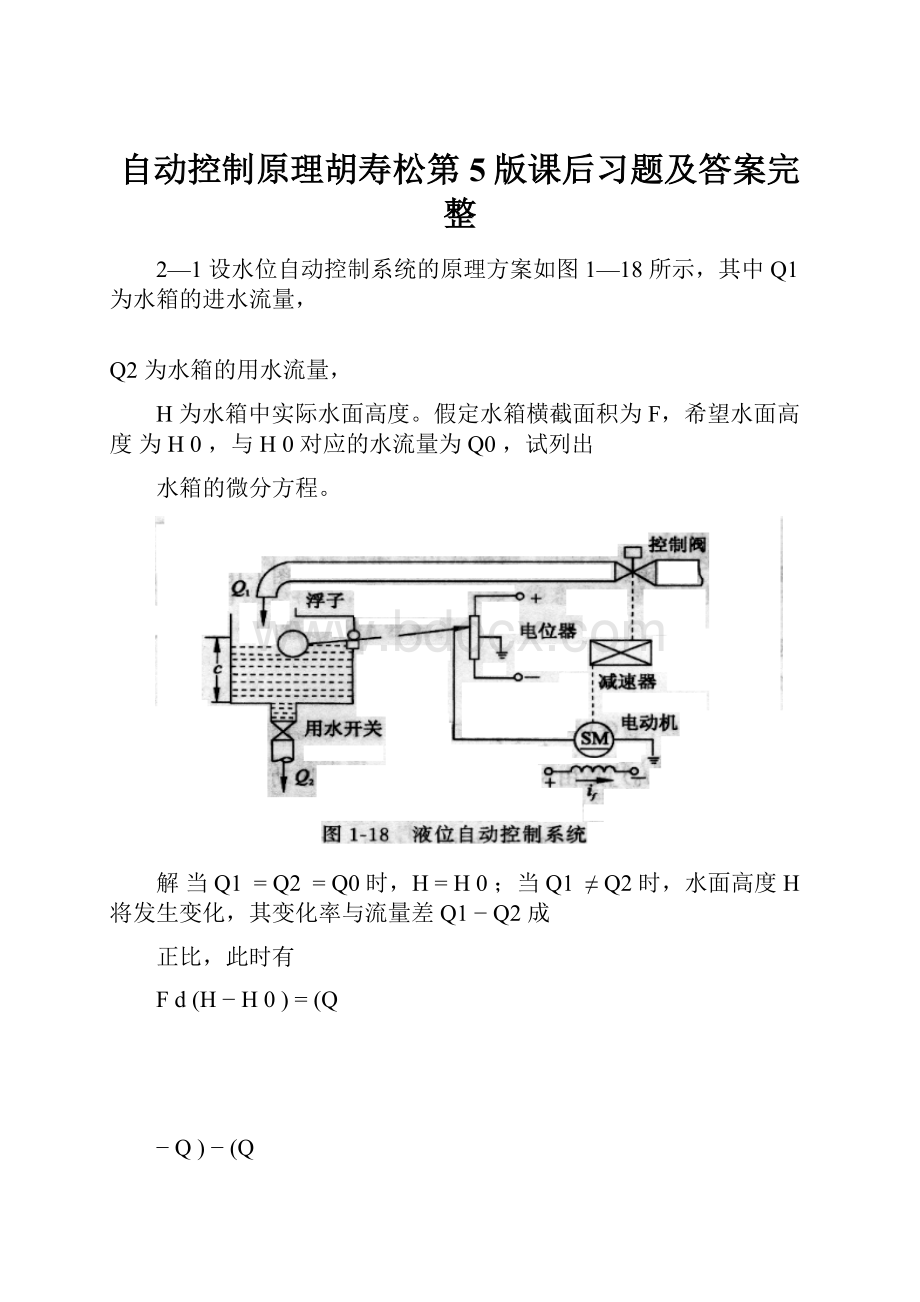
2—1设水位自动控制系统的原理方案如图1—18所示，其中Q1为水箱的进水流量，

Q2为水箱的用水流量，

H为水箱中实际水面高度。

假定水箱横截面积为F，希望水面高度为H0，与H0对应的水流量为Q0，试列出

水箱的微分方程。

解当Q1=Q2=Q0时，H=H0；当Q1≠Q2时，水面高度H将发生变化，其变化率与流量差Q1−Q2成

正比，此时有

Fd（H−H0）=（Q

−Q）−（Q

−Q）

dt1020

于是得水箱的微分方程为

FdH=Q−Q

dt12

2—2设机械系统如图2—57所示，其中xi为输入位移，x0为输出位移。

试分别列写各系统的微分方程式

及传递函数。

图2—57机械系统

解①图2—57（a）：

由牛顿第二运动定律，在不计重力时，可得

f1（x&i−x&0）−f2x&0=m&x&0

整理得

2

mdx0+（f

+f）dx0=f

dxi

dt2

12dt

1dt

将上式进行拉氏变换，并注意到运动由静止开始，即初始条件全部为零，可得

1

[ms2+（f

+f2

）s]X

0（s）=

f1sXi

（s）

于是传递函数为

X0（s）=

Xi（s）

f1

ms+f1+f2

②图2—57（b）：

其上半部弹簧与阻尼器之间，取辅助点A，并设A点位移为x，方向朝下；而在其下半部工。

引出点处取为辅助点B。

则由弹簧力与阻尼力平衡的原则，从A和B两点可以分别列出如下原始方程：

K1（xi−x）=

f（x&−x&0）

K2x0=

f（x&−x&0）

消去中间变量x，可得系统微分方程

f（K

+K）dx0+KKx

=Kf

dxi

12dt

120

1dt

对上式取拉氏变换，并计及初始条件为零，得系统传递函数为

X0（s）=

Xi（s）

fK1s

f（K1+K2）s+K1K2

③图2—57（c）：

以x0的引出点作为辅助点，根据力的平衡原则，可列出如下原始方程：

K1（xi−x）+f（x&i−x&0）=K2x0

移项整理得系统微分方程

fdx0+（K

dt1

+K2

）x0=

fdxi

dt

+K1xi

对上式进行拉氏变换，并注意到运动由静止开始，即

xi（0）=x0（0）=0

则系统传递函数为

X0（s）=

Xi（s）

fs+K1

fs+（K1+K2）

2-3试证明图2-58（ａ）的电网络与（b）的机械系统有相同的数学模型。

图2-58电网络与机械系统　

1

R1

1CsRR

解：

（a）：

利用运算阻抗法得：

Z

=R//

=1=1=1

11Cs

RCs+

Ts+

1R1

+1

C1s

11111

Z2=R2

+1

C2s

=1

C2s

（R2C2

s+1）=

1

C2s

（T2s+1）

U（s）Z

1

（T2s+1）

Cs

（Ts+1）（Ts+1）

所以：

0=2=2=12

Ui（s）

Z1+Z2

R1+

T1s+1

1

C2s

（T2s+1）

R1C2s+（T1s+1）（T2s+1）

（b）以K1和f1之间取辅助点A，并设A点位移为x，方向朝下；根据力的平衡原则，可列出如下原始方程：

K2（xi−x0）+f2（x&i−x&0）=

f1（x&0−x&）

（1）

K1x=

f1（x&0−x&）

（2）

所以K2（xi−x0）+f2（x&i−x&0）=K1x

对（3）式两边取微分得

K2（x&i−x&0）+f2（&x&i−&x&0）=K1x&

将（4）式代入

（1）式中得

（3）

（4）

K1K2（xi−x0）+K1f2（x&i−x&0）=K1f1x&0−f1K2（x&i−x&0）−f1f2（&x&i−&x&0）

整理上式得

f1f2&x&0+f1K2x&0+K1f1x&0+K1f2x&0+K1K2x0

=f1f2&x&i+f1K2x&i+K1f2x&i+K1K2xi

对上式去拉氏变换得

1

2

[ff

1

1

2

s2+（fK

2

+K1f1

+K1

0

f2）s+K1K2

]X（s）

1

2

=[f

fs2+（fK

+K1

f2）s+K1K2]X

i

（s）

所以：

X0（s）=

2

2

f1f2s

+（f1K2+K1f2）s+K1K2

f1f2

K1K2

=

s2+（f1

K

1

+f2）s+1

K2

Xi（s）

f1f2s

+（f1K2+K1f1+K1f2）s+K1K2

f1f2

K1K2

s2+

（f1

K

1

+f2）s+1+f1

K2K2

（f1

K

=1

s+1）（f2

K2

s+1）

（f1

K

1

s+1）（f2

K2

s+1）+f1

K2

所以图2-58（ａ）的电网络与（b）的机械系统有相同的数学模型。

2—4试分别列写图2-59中个无源网络的微分方程式。

解：

（a）:

列写电压平衡方程：

duCuC

ui−u0=uC

iC=C



dt

duC

uC

iR1=

R1

R



1

d（ui−u0）

ui−u0

u0=（iC+iR1）R2=C

+R2=C

+R2

整理得：



dt



R1dt

R1

CRdu0+CR2

0



+1u

=CR

dui

+CR2u



2dt

R1

2dti

（b）:

列写电压平衡方程：

duC1

ui−u0=uC1

（1）

iC1=C1

dt

（2）

iC2=

uC1+iC1RR

+iC1=

uC1

R

+2i

C1=C2

duC2

dt

=C2

d（u0−iC1R）

dt

（3）

即：

uC1

R

+2iC1=C2

d（u0−iC1R）

dt

2

（4）

将

（1）

（2）代入（4）得：

ui−u0+2C

d（ui−u0）=C

du0−CC

RduC1

R1dt

2dt

12dt2

uudu

dudu

d2u

d2u

即：

i−0+2C

i−2C

0=C

0−CC

Ri+CC

R0

RR

整理得：

1dt

1dt

2dt

12dt2

12dt2

2

CCRdu0C

Cdu0u0

CCRduiui

Cdui

12dt2

+（2+2

1）dt+R=12

2

dt2

++2

R

1dt

2-5设初始条件均为零，试用拉氏变换法求解下列微分方程式，并概略绘制x（t）曲线，指出各方程式的模态。

（1）

2x&（t）+x（t）=t;

解：

对上式两边去拉氏变换得：

（2s+1）X（s）=1/s2→X（s）=

1=1

s2（2s+1）s2

−1+

s

4

2s+1

运动模态e−0.5t

所以：

x（t）=t−2（1−e

−1t

2）

（２）&x&（t）+x&（t）+x（t）=™（t）。

解：

对上式两边去拉氏变换得：

（s2+s+1）X（s）=1→

X（s）=

1

（s2+s+1）

=1

（s+1/2）2+3/4

运动模态e

−t/2





t

3



sin

2

所以：

x（t）=

2e−t/2

3





t

3



sin

2

（3）&x&（t）+2x&（t）+x（t）=1（t）。

解：

对上式两边去拉氏变换得：

（s2+2s+1）X（s）=1→X（s）=

s

1=

s（s2+2s+1）

1

s（s+1）2

=1−

s

1+

s+1

1

（s+1）2

运动模态e−t（1+t）

所以：

x（t）=1−e−t−te−t

=1−e−t（1+t）

2-6在液压系统管道中，设通过阀门的流量满足如下流量方程：

Q=KP

式中K为比例常数，P为阀门前后的压差。

若流量Q与压差P在其平衡点（Q0,P0）附近作微小变化，试导出线性化

方程。

解：

设正常工作点为A，这时Q0=KP0

在该点附近用泰勒级数展开近似为：

y=f（x

）+df（x）

（x−x）



0dx



0

x0

即Q−Q0=K1（P−P0）

dQ

其中K1=

dP

=1K1

00

2

P=PP

2-7设弹簧特性由下式描述：

F=12.65y1.1

其中，是弹簧力；是变形位移。

若弹簧在变形位移附近作微小变化，试推导的线性化方程。

解：

设正常工作点为A，这时F=12.65y1.1

00

在该点附近用泰勒级数展开近似为：

y=f（x

）+df（x）

（x−x）



0dx



0

x0

即F−F0=K1（y−y0）

dF

其中

0.1

0.1

K1=

=12.65⋅1.1y0

=13.915⋅1.1y0

dy

y=y0

2-8设晶闸管三相桥式全控整流电路的输入量为控制角，输出量为空载整流电压，它们之间的关系为：

0

ed=Ed

cos〈

式中是整流电压的理想空载值，试推导其线性化方程式。

解：

设正常工作点为A，这时Ed

=Ed0cos〈0

在该点附近用泰勒级数展开近似为：

y=f（x

）+df（x）

（x−x）



0dx



0

x0

0

即ed−Ed

cos〈0=Ks（〈−〈0）

s

其中K=ded

d〈

=−Ed0sin〈0

〈=〈

2-9若某系统在阶跃输入r（t）=1（t）时，零初始条件下的输出响应c（t）=1−e−2t+e−t，试求系统的传递函数和脉冲响应。

解：

对输出响应取拉氏变换的：

C（s）=1−1

+1=

s2+4s+2

因为：

C（s）=√（s）R（s）=1√（s）

ss+2

s+1

s（s+1）（s+2）s

所以系统的传递函数为：

√（s）=

s2+4s+2（s+1）（s+2）

=1+

s

（s+1）（s+2）

=1−

1+

s+1

2

s+2

系统的脉冲响应为：

g（t）=™（t）−e−t+e−2t

2-10设系统传递函数为

C（s）

　　=

R（s）

2

s2+3s+2

且初始条件c（0）=-1,c&（0）＝０。

试求阶跃输入r（t）=1（t）时，系统的输出响应c（t）。

解：

由系统的传递函数得：

2

dc（t）+3dc（t）+2c（t）=2r（t）

（1）

dt2dt

对式

（1）取拉氏变换得：

s2C（s）−sc（0）−c&（0）+3sC（s）−3c（0）+2C（s）=2R（s）

将初始条件代入

（2）式得

（s2+3s+2）C（s）+s+3=21

s

（2）

即：

C（s）=

2−s2−3s

=

s（s2+3s+2）

2−2s+6

ss2+3s+2

=1−

s

4+

s+1

2

s+2

所以：

c（t）=2−4e−t+2e−2t

2-11在图2-60中，已知和两方框相对应的微分方程分别是

6dc（t）+10c（t）=20e（t）

dt

20db（t）+5b（t）=10c（t）

dt

且初始条件均为零，试求传递函数C（s）/R（s）及E（s）/R（s）

解：

系统结构图及微分方程得：

G（s）=

20

6s+10

H（s）=

10

20s+5

1020

E（s）1010

C（s）=

10G（s）

=6s+10

R（s）

==

1+G（s）H（s）

2010

R（s）

1+G（s）H（s）1+2010

1+

6s+1020s+5

6s+1020s+5

10（20s+5）（6s+10）

1200s2+1500s+500

0

=200（20s+5）

==200（20s+5）

==

（6s+10）（20s+5）+200

120s2+230s+250

（6s+10）（20s+5）+200

120s2+230s+250

2-12求图2-61所示有源网络的传递函数

1

解：

（a）Z0=R0//=

Cs

R1

C0s

1

=R0

Ts+1

T0=R0C0

R

00+

0

C0s

U0（s）=−R1

=−R1（Ts+1）

R

Ui（s）Z00

（b）Z0

=R0

0

0

//1=

Cs

R1

C0s

1

=R0

Ts+1

T0=R0C0

R

00+

0

C0s

11

Z=R+1

=T1s+1

T=RC

C1s

C1s

111

U0（s）=−Z1=−

1（Ts+1）（Ts+1）

U（s）Z

RCs10

i001

Z12

=R1

//（R2

+1

C2s

）=R1

//T2s+1

C2s

（c）

1

=

RT2s+1

C2s

=R1（T2s+1）

T2=R2C2

1

R+T2s+1

C2s

T2s+R1+1

U0（s）=−Z12

=−R1

T2s+1

Ui（s）R0

R0T2s+R1+1

2-13由运算放大器组成的控制系统模拟电路如图2-62所示，试求闭环传递函数Uｃ（ｓ）／Ｕｒ（ｓ）。

图2-62控制系统模拟电路　

解：

U1（s）

=−Z1

（1）

U2（s）=−Z2

（2）

U0（s）=−R2（3）

U0（s）+Ui（s）R0

U1（s）R0

U2（s）R0

式

（1）

（2）（3）左右两边分别相乘得

U0（s）

U0（s）+Ui（s）

=−Z1Z2

R0R0

R2即

R0

R

3

U0（s）+Ui（s）=−0

1+Ui（s）=−0

U0（s）

Z1Z2R2

U0（s）

Z1Z2R2

R

所以：

Ui（s）=−0−1

U0（s）

Z1Z2R2

R

3

R

+

0

R11

R

2

2

U0（s）=−1

=−Z1Z2R2

=−T1s+1C2s

U（s）R3

R3+ZZRR1

3

i0+1

Z1Z2R2

3

=−R1R2

0122

31RT1s+1C2s

（T1s+1）C2sR0

+R1R2

2-14试参照例2-2给出的电枢控制直流电动机的三组微分方程式，画出直流电动机的结构图，并由结构图等效变换求出电动机的传递函数Ωm（s）/Ua（s）和Ωm（s）/Mc（s）

解：

由公式（2-2）、（2-3）、（2-4）取拉氏变换

Ua（s）−Ea（s）=I

Ls+Ra

（s）

Ea（s）=CeΩm

（s）

aa

CmIa（s）=Mm（s）

m

Mm（s）−Mc（s）=Ω

（s）

Jms+fm

得到系统结构图如下：

Mc

Ua（s）

1Ia（s）CmMm

1Ωm（s）

－Las+RaJms+fm

Ce

Ωm（s）=

Cm

Las+Ra

1

Jms+fm=Cm

Ua（s）

1+CeCm

Las+Ra

1

Jms+fm

（Las+Ra）（Jms+fm）+CeCm

Ωm（s）=

Mc（s）1+

1

Jms+fm

CeCm1

=Las+Ra

（Las+Ra）（Jms+fm）+CeCm

Las+Ra

Jms+fm

2-15某位置随动系统原理方块图如图2-63所示。

已知电位器最大工作角度⎝

max

=330o，功率放大级放大系数为K3,要

求：

（1）分别求出电位器传递系数K0、第一级和第二级放大器的比例系数K1和K2；　

（2）画出系统结构图；　

（3）简化结构图，求系统传递函数⎝0（s）/⎝i（s）。

图2-63位置随动系统原理图　

解：

（1）K=15V

01650

K=30=3

110

K=20=2

210

（2）⎝e（s）=⎝i（s）−⎝0（s）

Us（s）=K0⎝e（s）

Ua（s）=K1K2KsUs（s）

Ua（s）=RaIa（s）+LasIa（s）+Eb（s）

Mm（s）=CmIa（s）

00mc

Js2⎝（s）+fs⎝（s）=M（s）−M（s）

系统结构图如下：

Eb（s）=Kb⎝0（s）

m

Mc

θiθe

－

θ0

0KKK

KUs12sUa

－Eb

1

Las+Ra

M－1θ0

Js2+fs

C

m