小学数学常见几何模型典型例题和解题思路.docx

小学数学常见几何模型典型例题和解题思路.docx

《小学数学常见几何模型典型例题和解题思路.docx》由会员分享，可在线阅读，更多相关《小学数学常见几何模型典型例题和解题思路.docx（13页珍藏版）》请在冰豆网上搜索。

小学数学常见几何模型典型例题和解题思路

小学数学常见几何模型典型例题及解题思路

（1）

巧求面积

常用方法：

直接求；整体减空白；不规则转规则（平移、旋转等）；模型（鸟头、蝴蝶、漏斗等模型）；差不变

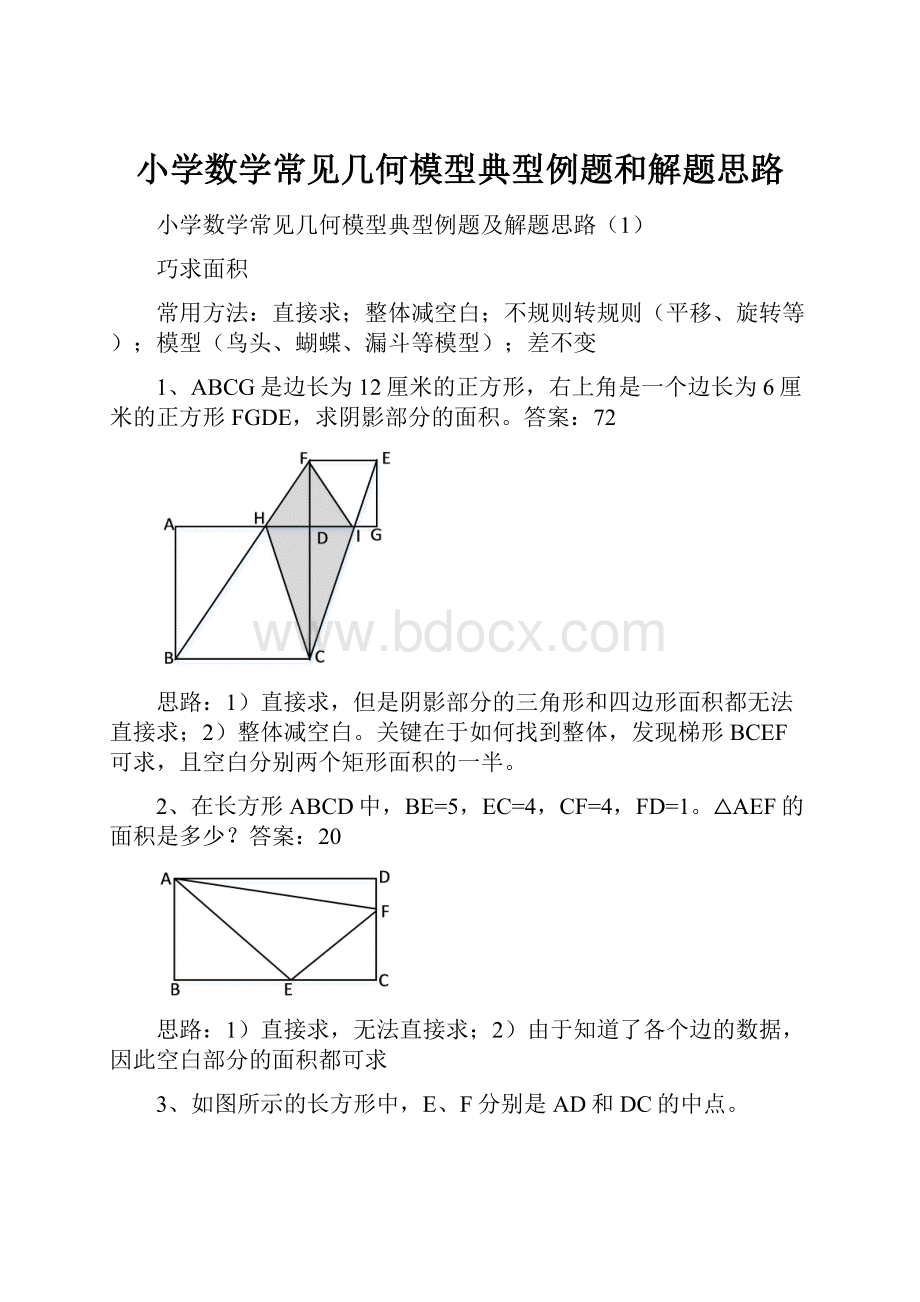
1、ABCG是边长为12厘米的正方形，右上角是一个边长为6厘米的正方形FGDE，求阴影部分的面积。

答案：

72

思路：

1）直接求，但是阴影部分的三角形和四边形面积都无法直接求；2）整体减空白。

关键在于如何找到整体，发现梯形BCEF可求，且空白分别两个矩形面积的一半。

2、在长方形ABCD中，BE=5，EC=4，CF=4，FD=1。

△AEF的面积是多少？

答案：

20

思路：

1）直接求，无法直接求；2）由于知道了各个边的数据，因此空白部分的面积都可求

3、如图所示的长方形中，E、F分别是AD和DC的中点。

（1）如果已知AB=10厘米，BC=6厘米，那么阴影部分面积是多少平方厘米？

答案：

22.5

（2）如果已知长方形ABCD的面积是64平方厘米，那么阴影部分的面积是多少平方厘米？

答案：

24

思路

（1）直接求，无法直接求；2）已经知道了各个边的数据，因此可以求出空白的位置；3）也可以利用鸟头模型

4、正方形ABCD边长是6厘米，△AFD（甲）是正方形的一部分，△CEF（乙）的面积比△AFD（甲）大6平方厘米。

请问CE的长是多少厘米。

答案：

8

思路：

差不变

5、把长为15厘米，宽为12厘米的长方形，分割成4个三角形，其面积分别为S1、S2、S3、S4，且S1=S2=S3+S4。

求S4。

答案：

10

思路：

求S4需要知道FC和EC的长度；FC不能直接求，但是DF可求，DF可以由三分之一矩形面积S1÷AD×2得到，同理EC也求。

最后一句三角形面积公式得到结果。

6、长方形ABCD内的阴影部分面积之和为70，AB=8，AD=15。

求四边形EFGO的面积。

答案10。

思路：

看到长方形和平行四边形，只要有对角线，就知道里面四个三角形面积相等。

然后依据常规思路可以得到答案。

思路2：

从整体看，四边形EFGO的面积=△AFC的面积+△BFD的面积-空白部分的面积。

而△ACF的面积+△BFD的面积=长方形面积的一半，即60。

空白部分的面积等于长方形面积减去阴影部分的面积，即120-70=50。

所以四边形的面积EFGO的面积为60-50=10。

比例模型

1、如图，AD=DB，AE=EF=FC。

已知阴影部分面积为5平方厘米，△ABC的面积是多少平方厘米？

答案30平方厘米。

思路：

由阴影面积求整个三角形的面积，因此需要构造已知三角的面积和其它三角形的面积比例关系，而题目中已经给了边的比，因此依据等高模型或者鸟头模型即可得到答案。

2、△ABC的面积是180平方厘米，D是BC的中点，AD的长是AE的3倍，EF的长是BF的3倍，那么△AEF的面积是多少平方厘米？

答案22.5平方厘米

思路：

仅仅告诉三角形面积和边的关系，需要依据比例关系进行构造各个三角形之间的关系，从而得出答案

3、在四边形ABCD中，E，F为AB的三等分点，G，H为CD的三等分点。

四边形EFHG的面积占总面积的几分之几？

答案是1/3

思路：

仅仅告诉边的关系，求四边形之间的关系，需要首先考虑如何分解为三角形，然后再依次求解。

4、在四边形ABCD中，ED：

EF：

FC=3:

2:

1，BG：

GH：

AH=3:

2:

1，已知四边形ABCD的面积等于4，则四边形EHGF的面积是多少？

答案4/3

5、在△ABC中，已知△ADE、△DCE、△BCD的面积分别是89,28,26，那么三角形DBE的面积是多少？

答案178/9

思路：

需要记住反向分解三角形，从而求面积。

6、在角MON的两边上分别有A、C、E及B、D六个点，并且△OAB、△ABC、△BCD、△CDE、△DEF的面积都等于1，则△DCF的面积等于多少？

答案3/4

7、四边形ABCD的面积是1，M、N是对角线AC的三等分点，P、Q是对角线BD的三等分点，求阴影部分的面积？

答案1/9

一半模型

比例模型---共高模型一半模型蝴蝶模型（漏斗，金字塔）鸟头模型燕尾模型风筝模型

切记梯形的一半模型（沿着中线变化）

切记任意四边形的一半模型

1、在梯形ABCD中，AB与CD平行，点E、F分别是AD和BC的中点。

△AMB的面积是3平方厘米，△DNC的面积是7平方厘米。

1）△AMB和△DNC的面积和等于四边形EMFN的面积；

2）阴影部分的面积是多少平方厘米。

思路：

一种应用重叠=未覆盖

思路：

将各个三角形标记，应用两个一半模型=整体梯形

2、任意四边形ABCD，E、F、G、H分别为各边的中点。

证明四边形EFGH的面积为四边形ABCD面积的一半。

3、四边形ABCD中，E、F、G、H分别是各边的中点。

求阴影部分与四边形PQRS的面积比。

答案相等

思路：

依次应用一半模型和重叠等于未覆盖。

证明需要分别连接BD和AC。

4、已知M、N分别为梯形两腰的中点，E、F为M、N上任意两点。

已知梯形ABCD的面积是30平方厘米，求阴影部分的面积。

答案：

15

5、已知梯形ABCD的面积是160，点E为AB的中点，DF：

FC=3:

5。

阴影部分的面积为多少。

答案：

30

鸟头模型

1、已知△ABC面积为1，延长AB至D，使BD=AB；延长BC至E，使CE=2BC，延长CA至F，使AF=3AC。

求△DEF的面积。

答案：

18

思路：

依次使用鸟头模型，别忘了最终还需要加上△ABC的面积。

2、在平行四边形ABCD中，BE=AB，CF=2CB，GD=3DC，HA=4AD，平行四边形的面积是2，四边形EFGH的面积是多少？

答案：

36

3、四边形EFGH的面积是66平方米，EA=AB，CB=BF，DC=CG，HD=DA，求四边形ABCD的面积？

答案：

13.2

4、将四边形ABCD的四条边AB、CB、CD、AD分别延伸两倍至点E、F、G、H，若四边形ABCD的面积为5，则四边形EFGH的面积是多少？

答案：

60

思路：

依次使用两类不同鸟头模型，别忘了最终还需要减去一个四边形ABCD的面积。

5、在三角形ABC中，延长AB至D，使BD=AB，延长BC至E，使CE=1/2BC，F是AC的中点，若三角形ABC的面积是2，则三角形DEF的面积是多少？

答案：

3.5

思路：

分割所求三角形，分别应用比例模型和鸟头模型。

6、△ABC中，延长BA到D，使DA=AB，延长CA到E，使EA=2AC，延长CB到F，使FB=3BC，如果△ABC的面积是1，那么△DEF的面积是多少？

答案：

7

思路：

△ABC和△EFC是鸟头模型，从而求出四边形ABEF的面积，△ABC和△AED是鸟头模型，从而求出△AED面积，从而

解题小技巧：

S1：

S2=S3：

S4

S1×S4=S2×S3

BO：

OD=S1：

S2=S3：

S4=（S1+S3）:

（S2+S4）

AO:

OC=?

1，答案为5

2、总面积为52，其中两个分别为6,7，另外两个分别是多少？

答案18,21

3、在△ABC中，已知M，N分别在AC、BC上，BM与AN相交于点O。

若△AOM，△ABO和△BON的面积分别是3,2,1，则△MNC的面积是多少？

答案22.5。

风筝模型求出△MON=1.5；

△ANM：

△MNC=△ABM：

△BMC

（3+1.5）：

x=（3+2）:

（1+1.5+x）