浙江省温岭市学大培训学校中考数学专题复习 27相似.docx

浙江省温岭市学大培训学校中考数学专题复习 27相似.docx

《浙江省温岭市学大培训学校中考数学专题复习 27相似.docx》由会员分享，可在线阅读，更多相关《浙江省温岭市学大培训学校中考数学专题复习 27相似.docx（16页珍藏版）》请在冰豆网上搜索。

浙江省温岭市学大培训学校中考数学专题复习27相似

27相似

一、知识性专题

专题1比例线段

【专题解读】解决有关比例线段的问题时，常常利用三角形相似来求解．

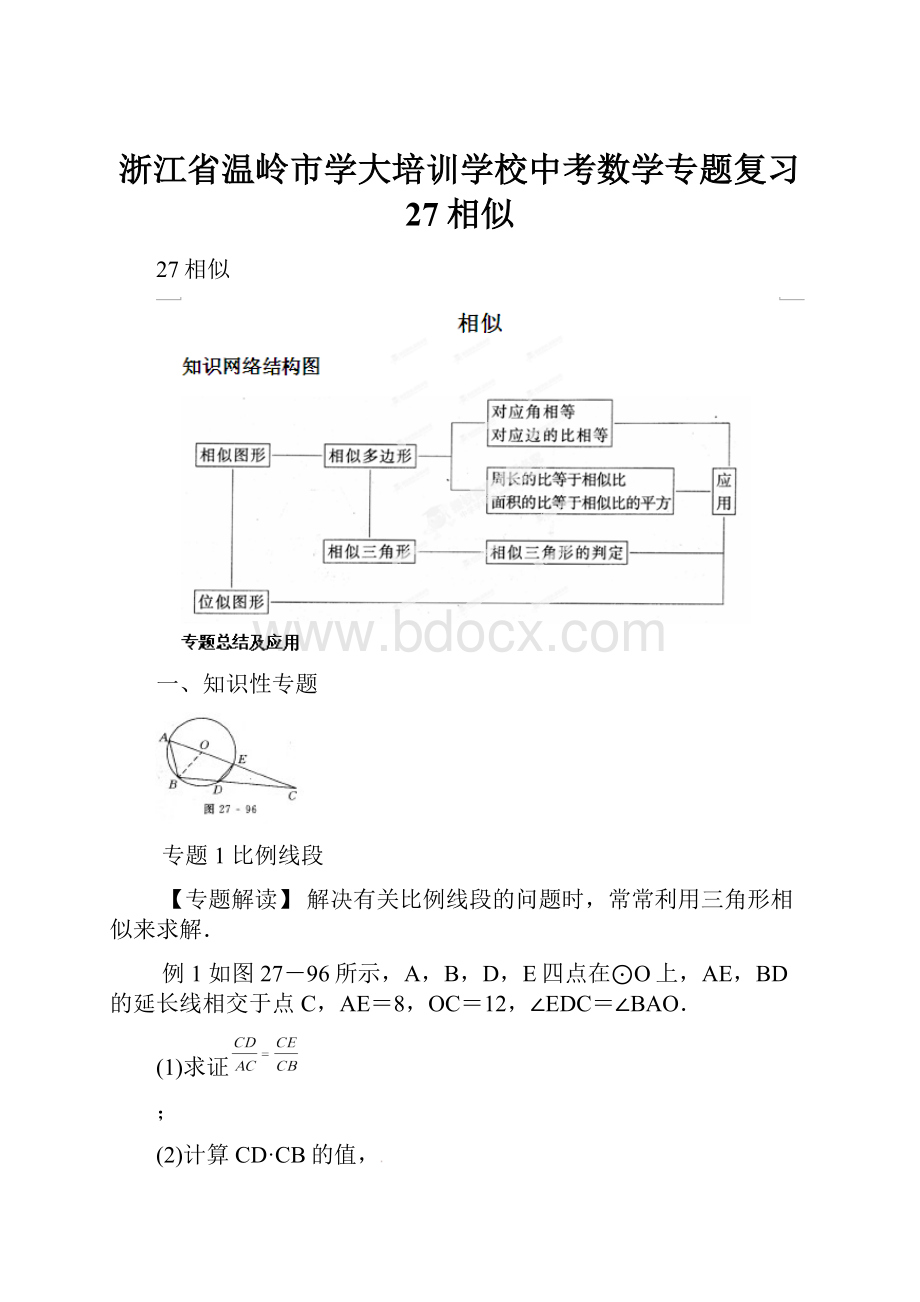
例1如图27－96所示，A，B，D，E四点在⊙O上，AE，BD的延长线相交于点C，AE＝8，OC＝12，∠EDC＝∠BAO．

（1）求证

；

（2）计算CD·CB的值，

并指出CB的取值范围．

专题2乘积式或比例式的证明

【专题解读】证明形如

，

或

=1的式子，常将其转化为若干个比例式之积来解决．如要证

，可设法证

，

，然后将两式相乘即可，这里寻找线段x便是证题的关键。

例2如图27－97所示，在等腰三角形ABC中，过A作AD⊥BC，过C作CE⊥AB，又作DF⊥CE，FG⊥AD，求证

．

例3如图27－98所示，在△ABC中，已知∠A：

∠B：

∠C=1：

2：

4，求证

.

二、规律方法专题

专题3：

相似三角形的性质

【专题解读】相似三角形是初中数学重要的内容之一，其应

用广泛，可以证明线段相等、平行、垂直，也可以计算图形的面积及线段的比值等，解题的关键是识别（或构造）相似三角形的基本图形．

例4如图27－99所不，在△ABC中，看DE∥BC，

，DE＝4cm，则BC的长为（）

A．8cmB．12cm

C．11cmD．10cm

例5如图27－100所示，在△ABC中，AB＝BC＝12cm，∠ABC＝80°，BD是∠ABC的平分线，DE∥BC.

（1）求∠EDB的度数；

（2）求DE的长．

【解题策略】将比例式中的AE转化为AB－DE，逐步由未知转化为已知，建立关于DE的关系式来求解．

例6如图27－101所示，点D，E在BC上，且FD∥AB，FE∥AC，求证△ABC∽△FDE．

例7如图27

－102所示，已知点正是矩形ABCD的边CD上一点，BF⊥AE于点F，求证△ABF∽△EAD．

三、思想方法专题

专题4分类讨论思想

【专题解读】分类讨论思想是一种重要的数学思想，我们在研究问题的解法时，应把可能

出现的各种情况都加以考虑，这样才能全面、严谨地思考问题．

例8在△ABC中，AB＞BC＞AC，D是AC的中点，过点D作直线l，使截得的三角形与原三角形相似，这样的直线l有条．

专题5建模思想

【专题解读】本章建模思想多用于将实际问题转化为几何图形，然后根据相似的性质解决问题．

例

9如图27－104所示，小明想用皮尺测量池塘A，B间的距离，但现有皮尺无法直接测量池塘A，B间的距离，学习有关的数学知识后，他想出了一个主意，先在地面上取一个可以直接到达A，B两点的点O，连接OA，OB，分别在OA，OB上取中点C，D，连接CD，并测得CD＝a，由此他知道A，B间的距离是（）

A．

aB．2aC．aD．3a

例10如图27－105所示，九年级

（1）班课外活动小组利用标杆测量学校旗杆的高度，已知标杆高度CD＝3m，标杆与旗杆的水平距离BD＝15m，人的眼睛与地面的高度EF＝1．6m，人与标杆CD的水平距离DF＝2m，求旗杆AB的高度．

专题6转化思想

【专题解读】本章中的转化思想主要用于解决一些比例线段的问题．

例11如图27－106所示，已知E为

ABCD的边CD延长线上的一点，连接BE交AC于O，交AD于F

．求证BO2＝OF·OE．

例12在△ABC和△DEF中，AB＝2DE，AC＝2DF，∠A＝∠D，如果△ABC的周长是16，面积是12，那么△DEF的周长、面积依次为（）

A．8，3B．8，6C．4，3D．4，6

例13已知△ABC与△DEF相似且面积比为4：

25，则△ABC与△DEF的相似比为．

例14已知△ABC∽△A′B′C′，且S△ABC：

S△A′B′C′＝1：

2，则AB：

A′B′＝．

中考真题精选

1.将左下图中的箭头缩小到原来的

，得到的图形是（　　）

2.某校每位学生上、下学期各选择一个社团，下表为该校学生上、下学期各社团的人数比例．若该校上、下学期的学生人数不变，相较于上学期，下学期各社团的学生人数变化，下列叙述何者正确？

（　　）

舞蹈社

溜冰社

魔術社

上學期

3

4

5

下學期

4

3

2

A、舞蹈社不变，溜冰社减少B、舞蹈社不变，溜冰社不变

C、舞蹈社增加，溜冰社减少D、舞蹈社增加，溜冰社不变

3.如图，梯形ABCD中，AD∥BC，E、F两点分别在AB、DC上．若AE=4，EB=6，DF=2，FC=3，且梯形AEFD与梯形EBCF相似，则AD与BC的长度比为何？

（　　）

A、1：

2B、2：

3

C、2：

5D、4：

9

4.两个相似多边形的面积比是

，其中较小多边形周长为36cm，则较大多边形周长为（）

A．48cmB．54cmC．56cmD．64cm

5.已知菱形ABCD的边长为1，∠ADC=60º，等边△AEF两边分别交DC、CB于点E、F。

（1）（4分）特殊发现：

如图1，若点E、F分别是DC、CB的中点，求证菱形ABCD对角母AC、BD的交点O即为等边△AEF的外心；

（2）若点E、F始终分别在边DC、CB上移动，记等边△AEF的外心为点P。

①（4分）猜想验证：

如图2，猜想△AEF的外心P落在哪一直线上，并加以证明；

②（5分）拓展运用：

如图3，猜想△AEF面积最小时，过点P任作一直线分别交边DA于点M

，交边DC的延长线于点N，试判断

是否为定值，若是，请求出该定值；若不是，请说明理由。

6.已知：

如图所示的一张矩形纸片ABCD（AD>AB），将纸片折叠一次，使点A与点C重合，再展开，折痕EF交AD边于点E，交BC边于点F，分别连结AF和CE。

（1）求证：

四边形AFCE是菱形；

（2）若AE=10cm，△ABF的面积为24cm2，求△ABF的周长；

（3）在线段AC上是否存在一点P，使得2AE2=AC·AP？

若存在，请说明点P的位置，并予以证明；若不存在，请说明理由.

7.如图是小红设计的钻石形商标，△ABC是边长为2的等边三角形，四边形ACDE是等腰梯形，AC∥ED，∠EAC=60°，AE=1．

（1）证明：

△ABE≌△CBD；

（2）图中存在多对相似三角形，请你找出一对进行证明，并求出其相似比（不添加辅助线，不找全等的相似三角形）；

（3）小红发现AM=MN=NC，请证明此结论；

（4）求线段BD的长．

8.某课题学习小组在一次活动中对三角形的内接正方形的有关问题进行了探讨：

定义：

如果一个正方形的四个顶点都在一个三角形的边上，那么我们就把这个正方形叫做三角形的内接正方形．

结论：

在探讨过程中，有三位同学得出如下结果：

甲同学：

在钝角、直角、不等边锐角三角形中分别存在　　个、　　个、　　个大小不同的内接正方形．

乙同学：

在直角三角形中，两个顶点都在斜边上的内接正方形的面积较大．

丙同学：

在不等边锐角三角形中，两个顶点都在较大边上的内接正方形的面积反而较小．

任务：

（1）填充甲同学结论中的数据；

（2）乙同学的结果正确吗？

若不正确，请举出一个反例并通过计算给予说明，若正确，请给出证明；

（3）请你结合

（2）的判定，推测丙同学的结论是否正确，并证明．

9.某数学兴趣小组开展了一次活动，过程如下：

设∠BAC=θ（0°＜θ＜90°）小棒依次摆放在两射线之间，并使小棒两端分别落在两射线上．

活动一：

如

图甲所示，从点A1开始，依次向右摆放小棒，使小棒与小棒在端点处互相垂直，A1A2为第1根小棒．

数学思考：

（1）小棒能无限摆下去吗？

答：

能（填“能“或“不能”）

（2）设AA1=A1A2=A2A3=1．

①θ=22.5度；

②若记小棒A2n-1A2n的长度为an（n为正整数，如A1A2=a1，A3A4=a2，…），求出此时a2，a3的值，并直接写出an（用含n的式子表示）．

活动二：

如图乙所示，从点A1开始，用等长的小棒依次向右摆放，其中A1A2为第1根小棒，且A1A2=AA1．

数学思考：

（3）若已经向右摆放了3根小棒，则θ1=2θ，θ2=3θ，θ3=4θ（用含θ的式子表示）；

（4）若只能摆放4根小棒，求θ的范围．

综合验收评估测试题

（时间：

120分钟满分：

120分）

一、选择题

1．要做甲、乙两个形状相同（相似）．的三角形框架，已知三角形框架甲的三边长分别为50cm，60cm，80cm，三角形框架乙的一边长为20cm，那么符合条件的三角形框架乙共有（）

A．1种B．2种C．3种D．4种

2．

如图27－107所示，在△ABC中，已知∠AED＝∠B，DE＝6，AB＝10，AE＝8，则BC的长为（）

A.

B．7C．

D.

3．如图27－108所示，在△ABC中，D，E分别为AB，AC的中点，若△ABC的面积为12cm2，则△ADE的面积为（）

A．2cm2B．3cm2C．4cm2D．6cm2

4．厨房角柜的台面是三角形，如果把各边中点的连线所围成的三角形铺上黑色大理石，如图27—109所示，其余部分铺上白色大理石，那么黑色大理石与白色大理石的面积比为（）

A．1：

4B．4：

1C．1：

3D．

3：

4

5．如图27－110所示，D是△ABC的边AB上一点，过D作DE∥BC交AC于E，若AD：

DB＝2：

3，则S△ADE：

S四边形BCED等于（）

A．2：

3B．4：

9C．4；5D．4：

21

6．如图27－111所示，DE是△ABC的中位线，F是DE的中点，BF的延长线交AC于点H，则AH：

HE等于（）

A．1：

1B．2：

1C．1：

D．3：

2

7．△ABC的三边长分别为

，

，2，△A′B′C′的两边长分别为1和

，如果△ABC∽△A′B′C′，那么△A′B′C′的第三边长应为（）

A.

B．

C.

D．

8．如图27－112所示，在△ABC中，DE∥BC，且S△ADE＝S四边形BDEC，则DE：

BC等于（）

A．1:

2B．

：

2C．1：

4D．2：

3

9．如图27－113所示，在

ABCD中，CE是∠DCB的平分线，F是AB的中点，AB＝6，BC＝4，则AE：

EF：

FB等于（）

A．1：

2：

3B．2：

1：

3C．3：

2：

1D．3：

1：

2

10．点P是△ABC中AB边上的一点，过点P作直线（不与直线AB重合）截△ABC，使截得的三角形与原三角形相似，则满足这样条件的直线最多

有（）

A．2条B．3条C．4条D．5条

二、填空题

11．如图27－114所示，在△ABC中，DE∥BC交AB于D，交AC于E，若AD＝3.2，DB＝2.4，AE＝2.8，则AC＝．

12．一根2米长的竹竿直立在操场上，影长为1.6米，在同一时刻，测得旗杆的影长为17．6米，则旗杆高米．

13．若△ABC∽△A′B′C′，AC＝5，A′C′＝8，则S△ABC：

S△A′B′C′

=．

14．已知两个相似多边形的一组对应边长分别为3cm和4cm，如果它们的面积和为50cm2，则较大多边形的面积为cm2．

15．若一个多边形在图上的面积为4cm2，比例尺为1：

1000，则该多边形的实际面积为m2．

16．已知△ABC∽△DEF，相似比为3，△ABC的周长为54cm，若△DEF的三边长之比为2：

3：

4，则△DEF的最短边长为cm．

三、解答题

17．如图27－115所示，在△ABC中，AB＝8，AC＝6，点D在AC上，且AD＝2，在AB上找一点E，使得△ADE与原三角形相似，这样的点E有几个?

求出AE的长．

18．如图27－116所示，已知在矩形ABCD中，AB＝5，AD＝20，点M分BC为BM：

MC＝1：

2，DE⊥AM于点E，求DE的长．

19．如图27－117所示，在矩形ABCD中，AB＝4，BC＝6，M是BC的中点，DE⊥AM，垂足为E，求DE的长．

20．如图27－118所示，在△ABC中，已知AB＝AC＝8，BC＝6，BD⊥AC于D，AE⊥BC于E，求CD的长．

21．如图27－119所示，已知CD是Rt△ABC的斜边AB上的高，若AD＝10，BD＝5，求CD的长．

22．如图27－120所示，在△ABC中，DE∥BC，且S△ADE：

S四边形BCE

D＝1：

3，求AD：

DB．

23．在Rt△ABC中，CD为斜边上的高，试确定AC是哪两条线段的比例中项，用比例式或等积式写出你的结论，并加以证明．

24．如图27－121所示，在正方形ABCD中，E是AB上一点，EF⊥CE交AD于F．

（1）求证△AEF∽△BCE；

（2）求证

.

25．如图27－122所示，已知∠ABC＝∠CDB＝90°，AC＝a，BC＝b．

（1）当BD与a，b之间满足怎样的关系时，△ABC∽△CDB；

（2）过A作BD的垂线，与DB的延长线交于点E，若△ABC∽△CDB

，试判断四边形AEDC是什么四边形．

26．如图27－123所示，在△ABC中，AB＝5，BC＝3，AC＝4，PQ∥AB，点P在AC上，点Q在BC上．

（1）当△PQC的面积与四边形PABQ的面积相等时，求CP的长；

（2）当△PQC的周长与四边形PABQ的周长相等时，求CP的长；

（3）在AB上是否存在点M，使△PQM为等腰直角三角形?

若存在，求出PQ的长；若不存在，请说明理由．