习题选解微波网络基础.docx

习题选解微波网络基础.docx

《习题选解微波网络基础.docx》由会员分享，可在线阅读，更多相关《习题选解微波网络基础.docx（20页珍藏版）》请在冰豆网上搜索。

习题选解微波网络基础

第4章微波网络基础

习）

[1]为什么说微波网络方法是研究微波电路的重要手段微波网络与低频网络相比较有哪些异同点

[2]表征微波网络的参量有哪几种分别说明它们的意义、特征及英相互间的关系。

[3]二端口微波网络的主要工作特性参量有哪些它们与网络参量有何关系

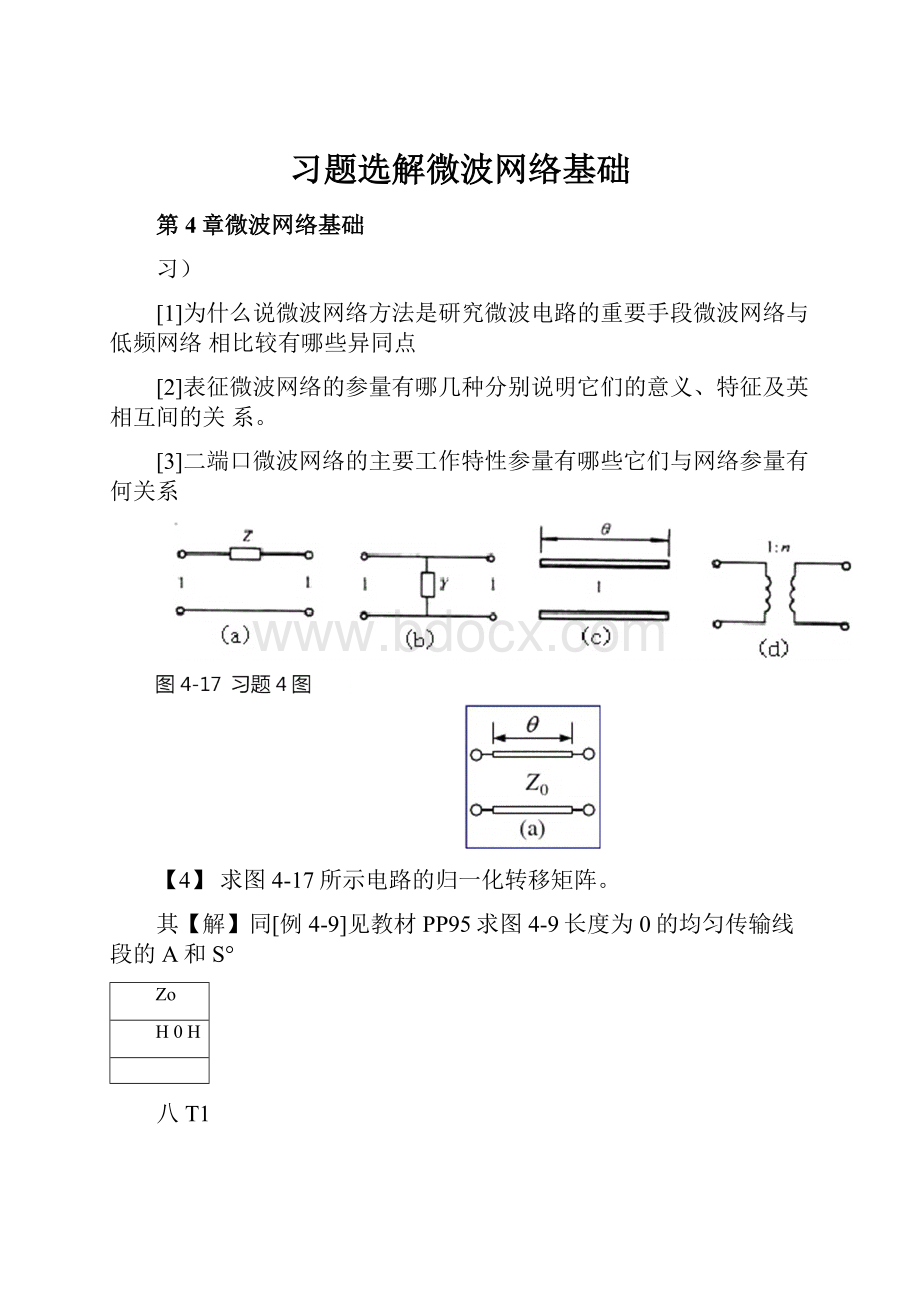
【4】求图4-17所示电路的归一化转移矩阵。

其【解】同[例4-9]见教材PP95求图4-9长度为0的均匀传输线段的A和S°

Zo

H0H

八T1

图4-9长度为&的均匀传输线段

U[=A[lU2-Ai2l2

71=A2lU2^A22I2

先确宦A矩阵。

当端口

（2）开路（即心=0）时，人面为电压波腹点，令则〃严仏（舁+e〃）=（4cos&,且此时端口⑴的输入阻抗为Z.a=-jZocot0.

2

由A矩阵的立义得：

n4/.t/./z

=cos0,=—=—-

U.

L-02

旦==_避ZU2一必cot他Zo

cos3

in

当端口⑵短路（即吩。

〉时,砌为电压波节点，令宀宀则

〃产牛（舁一不"卜"mSin。

，且此时端口⑴的输入阻抗为Z测=）Z（1tan^o由A矩阵的圧义得：

4=£l=

7-/

=jZ（、sin0,A^=—

L也--/

nd®y>-o'丹

也可以利用网络性质求

由网络的对称性得：

A22=^,=005/9

再由网络可逆性得：

人「=月”班_]=2、0一]=jZMA2}jsinO/Z{}

于是长度为0的均匀传输线段的A矩阵为

cos0jZ0sin0

ysin^/Z0cos0

如果两端口所接传输线的特性阻抗分别为Z。

】和乙龙，则归一化A矩阵为

互COS0

Z（）i

.JZoZo?

sin&

J疋-

.Zosin0

经COS0

Z°2

当Z（m=Z°2=Z（）时

cos0Jsin0

jsin&cos6

[6]（返回）求图4-19所示h型网络的转移矩阵。

I.

ylv2

——o

图4-19习题6图

【解】（返回）汁算的方法有两种:

方法一：

根据泄义式计算；方法二：

如下，分解的思想。

思路：

分解成如图所示的单元件单元电路，之后利用级联网络转移矩阵。

去Zz2厶/2

O—►—Wv—

vj山％!

討1叫

OOO1O

转移矩阵的关系式为：

5=內心2-内2*2

/]=人21〃2-人22丿2

根据电路理论，得出两个子电路的电压电流关系，并与泄义式对比后得出两个子电路的转移矩阵A1和A2分别为：

!

\=-/2

—

I1=YU2-I2

（a）

先根据左义il•算形如上图电路的阻抗矩阵为：

Z=Z]+ZgZ3

Z3Z2+Z3

将G）图与之对比，得（a）图阻抗矩阵为：

问+**・

1

'j'jcoCjcoC

Z]=jo）L、厶=U.Zq=n

jcoC

1I

jaCjcoC

先根据左义讣算形如上图电路的导纳矩阵为:

:

i2=y21v[+y22v2

3糾宀計迸

妇・（m）

=

11

jcoLjcoL

1ja）C+1ja）LJjcoL

1

，丄_阿丫_S

12匕％丄11片+人+片

在（G图中乙=丄，5=丿・处，场=8,代入上式得:

jcoL

（b）

将（b）图与之对比，得（b）图阻抗矩阵为：

Zj=JC0L.Z2=jcoL工、=

n

Z⑷=

T^c

1-/LC

丿2讥-j^I?

C

jl^L-jc^DC

jML-j^lJC

j23L-jc^l3c

因为:

REF

^11=^2=

/、+jx0

”（”+h）jeL'jcoL1-少厶C

^12=bi=

]

2ja）L-j（^I?

C

IjcoL-jayljC

图表1

[8]求图4-21所示电路的散射矩阵。

o~

z°丁cz。

g丄>_o

（b）

图4-21习题8图

【解】（返回）

（a）

0

e"

e~ie

0

（b）

査表4-2知单个并联电容（导纳）构成网络的S参数:

Z。

O

yz°

O

2+y

2

.2+y

2+y

-v

277,

其中y=jcoc/Y^

利用参考而移动对S参数的影响，可得,

'e~jd0-

•-y

2+y

2

2+y

0

"一yg-j”

2+y

2e-j20

2+y

■-y2"I

0e-jd_

2

y

0

e~ie_

2严

—儿厂必

2+y

.2-y]

〔2+y

2+〉J

.2+y

2+yJ

其中S11=S22,

S12=S21：

矩阵相乘得:

11丄2+y2Y0+jcoc

=S“=丄不妙=%严

2+y2Y0^ja）c

（沧其中为归一化特性导纳且Yq=1/ZO）o

【10】用z、Y.A、S参量分别表示可逆二端口微波网络和对称二端口微波网络的

特点。

1.可逆网络（互易网络）

Z12=Z21或Zi2=Z：

i

Yn=Y2l或K12=r2i

Sn=S2\

2.对称网络

Z\\=Z=

或

Zu=Zr

或

5!

1=522

Al=412（An=An）o

人血-人2九产1或

AnAn-AnAi]=1

【13】求图4-24所示电路中7；与耳参考面所确定网络的归一化转移参量矩阵和归

【解】

思路：

把原电路分解成单元电路，并利用单元电路结果（表4-2）、参量矩阵转换及级联网络A矩阵特点进行计算。

（a）详解：

其中等效的并联归一化输入导纳为：

Yp=ycot/7/=jcot—-=j

査表4-2知，单个并联导纳网络的归一化转移参量：

A=A3=

传输线的归一化转移参量：

入厂鶯詈：

］，几/4对应的&为;r/2。

利用表4-1的转换公式计算归一化散射参量矩阵：

detA=AiiA22-Ai2A2i

中间段是短路短截线,

Zi厂jZw0=jZo・•・0/=砒4

第1和第3是短路短截线.

Z-J=jZotai1/7/=jZo•.•01=屮

••・5=1/闷=一必）

总的归一化转移参量:

S]]=

Aw+A12一A21一Ay

A\\+A\2+An+An

S]2=

2detA

An+An+A21+A22

^21=

2

A11+Ah+A21+A22

S21=

-Aii+A12-A”+屉

Ah+412+A21+A22

Ah+A\i--An=4/

detA=l

An+Au+A：

\+A22=4-2/-An+An-A21+An=4/

耳「2+盯

2-丿

5

s-1

2+j

"-2+4；2+j

c・

2-丿

5

S=

55

s-1

2+j

2+j-2+4j

r2_j

5

.55

s、、=f

“2-j

-2+4j

5

【14】如图4-25所示二端口网络参考面耳处接归一化负载阻抗Z-而A-人2、

A21.A22为二端口网络的归一化转移参量，试证明参考而7；处的输入阻抗为:

【证明】

回顾总义:

U1=AwUi+Ai2（—7z）

/1=A1\U2+A22（-/l）

A=

A.

a2'

A=

Ai人2

a2Ia22

简记为:

因为：

Zz.=2-,代入上式即得：

Zin=‘1-

—人A1\Zl+A22

［19］已知二端口网络的散射参量矩阵为:

「0.2""0.98/

S=

0.98屮0・2/也

求二端口网络的插入相移8.插入衰减厶（dB）、电压传输系数T及输入驻波比°°

【解】

0=argT=argS“=兀

T=S21=0.9必

l+|Sj_l+0.2一

1-|SH|1-0.2

J2J2

OA占二•占V¥

v.lr0LIy应

o11o

（a）

习题

图4-18习题5图

6.求图4-19所示兀型网络的转移矩阵。

图4-19习题6图

7.求图4-20所示电路的Z矩阵和Y矩阵。

图4-20习题7图

8.求图4-21所示电路的散射矩阵。

（a）

图4-21习题8图

9.求图4-22所示电路参考而7；和耳间的归一化转移矩阵。

并说明在什么条

件下插入此二端口网络不产生反射

图4-22习题9图

10.用Z、Y、A、S参量分别表示可逆二端口微波网络和对称二端口微波网络的特点。

11.试用网络矩阵形式证明：

终端接任意负载乙_、电长度为&、特性阻抗为Z。

的短截线，其输入阻抗为

Zl+jZ°伽&

Zo+jZLtan6

12.设有一传输线，其特性阻抗为Zo,长度为/•可用T型或口型集总参数网络

来等效，如图4-23所示。

试推导图中（a）与（b）及（a）与（c）的等效关系。

当短截线长度7<2/8时，其等效关系可以简化。

由简化关系可以得出什么结论

13.

求图4-24所示电路中7；与耳参考面所确左网络的归一化转移参量矩阵和归一化散射参量矩阵。

图4-24习题13图

14.如图4-25所示二端口网络参考面7；处接归一化负载阻抗Z-而An.人2、

■

A2i.A22为二端口网络的归一化转移参量，试证明参考而7；处的输入阻抗为

Zin=

_AwZl+An

Ai\Zl+A22

图4-25习题14图

15.如图4-26所示的可逆二端口网络参考而匚处接负载导纳乙，试证明参考而£

处的输入导纳为

Yin=Yn-

16.如图4-27所示的可逆二端口网络参考而7；接负载阻抗Z一证明参考而7；处

的输入阻抗为

"It2

图4-27习题16图

17.如图4-28所示，一可逆二端口网络，从参考而7；.7；向二口网络、向负

载方向的反射系数分别为r;与试证明:

（i）r=sn+2

111i-s』

（2）若参考面7；为短路、开路和匹配时，分别测得的I；为r15.匚。

和rIC,则有

Sj

门一i厂2

1—

11

可逆二口网络

F2

1

1

1

T\

Ti

图4-28习题17图

18.如图4-29所示可逆对称无耗二端口网络参考面3接匹配负载，测得距参考而久距离为心0・125外处是电压波节，驻波比q=1・5,求二端口网络的散射参量矩阵。

图4-29习题18图

19.已知二端口网络的散射参量矩阵为s_|~0.2严门0.98H'T'

&0.98/02严2

求二端口网络的插入相移6L插入衰减LQIBX电压传输系数T及输入驻波比°。

20.已知一个可逆对称无耗二端口网络，输出端接匹配负载，测得网络输入端的反射系数为匚=0・8"",试求：

（1）S]]、S]2、5*22:

（2）插入相移&、插入衰减L（dB）、电压传输系数T及输入驻波比°°

21.已知二端口网络的转移参SAu=A22=1,人2=丿乙〉，网络外接传输线特性阻抗为乙），求网络输入驻波比p。

22.如图4-30所示，参考而7；、人所确怎的二端口网络的散射参量为几、S'—

S21及S?

?

，网络输入端传输线上波的相移常数为0。

若参考而7；外移距离/至7；处，求参考面A、G所确定的网络的散射参量矩阵S：

!

!

[S||S|2]

IS21S22」

1

1

11

III

T{Tx

图4-30习题22图

23.如图4-31所示参考而7；、7；及7；所确泄的三端口网络的散射参量矩阵为

若参考而7；内移距离4至人处，参考而耳外移距离人至人处，参考而人位置不

变，求参考而7；、人及7；所确沱的网络的散射参量矩阵S'。

一门（巧）

I；三端口

!

；微波网络II

It|Ji]

八T\T2T{

图4-31习题23图