逻辑代数化简练习.docx

逻辑代数化简练习.docx

《逻辑代数化简练习.docx》由会员分享，可在线阅读，更多相关《逻辑代数化简练习.docx（20页珍藏版）》请在冰豆网上搜索。

逻辑代数化简练习

逻辑代数化简练习

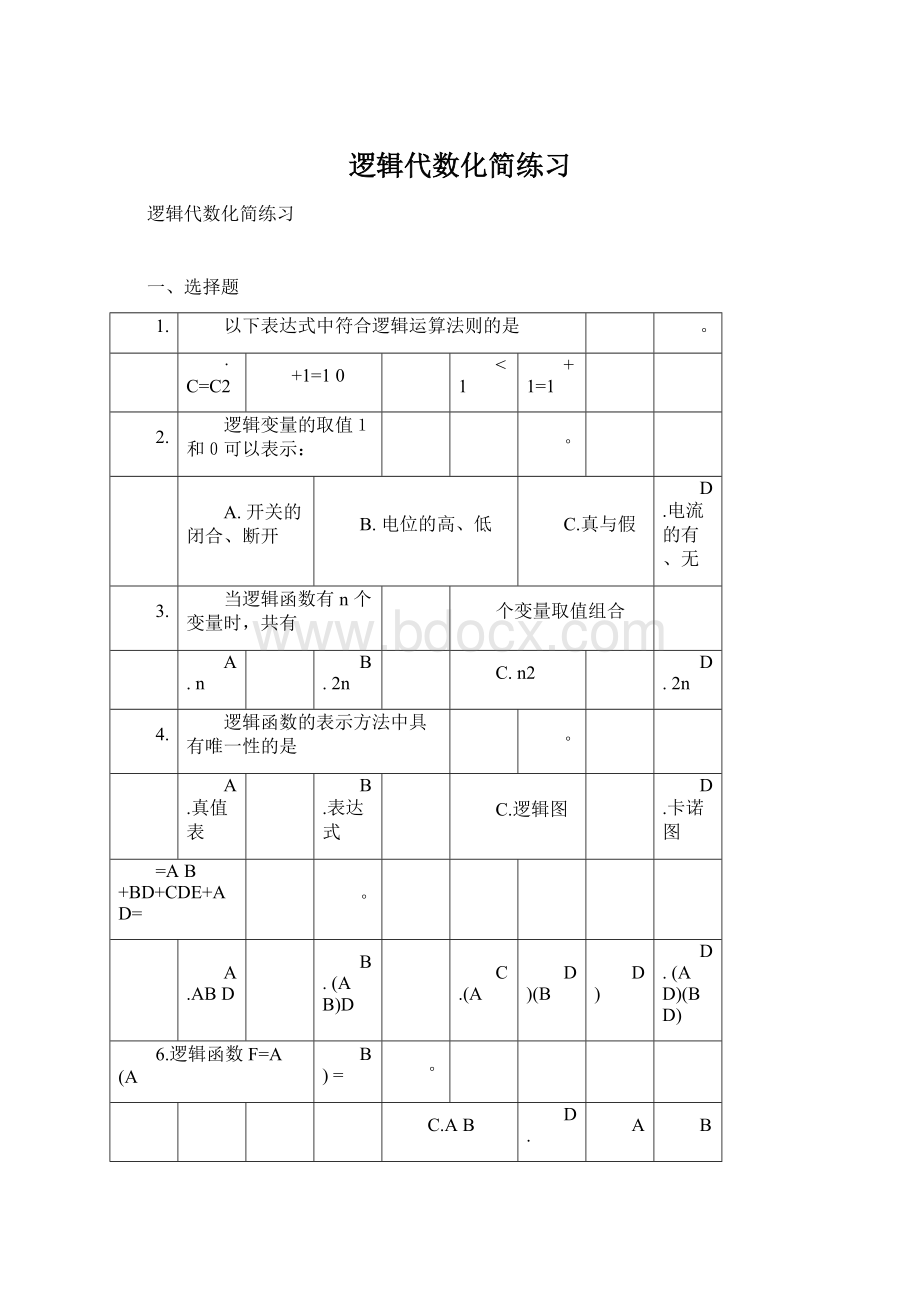
一、选择题

1.

以下表达式中符合逻辑运算法则的是

。

·C=C2

+1=10

<1

+1=1

2.

逻辑变量的取值１和０可以表示：

。

A.开关的闭合、断开

B.电位的高、低

C.真与假

D.电流的有、无

3.

当逻辑函数有n个变量时，共有

个变量取值组合

A.n

B.2n

C.n2

D.2n

4.

逻辑函数的表示方法中具有唯一性的是

。

A.真值表

B.表达式

C.逻辑图

D.卡诺图

=AB+BD+CDE+AD=

。

A.ABD

B.（AB）D

C.（A

D）（B

D）

D.（AD）（BD）

6.逻辑函数F=A（A

B）=

。

C.AB

D.

A

B

7．求一个逻辑函数

F的对偶式，可将

F中的

。

A.“·”换成“+”，“+”换成“·”

D.常数中“0”换成“1”，“1”换成“

E.常数不变

8．A+BC=。

0”

A.A+B+CC.（A+B）（A+C）+C

9．在何种输入情况下，“与非”运算的结果是逻辑0。

A．全部输入是0B.任一输入是0C.仅一输入是0D.全部输入是

10．在何种输入情况下，“或非”运算的结果是逻辑0。

A．全部输入是0B.全部输入是1C.任一输入为0，其他输入为

1

1

D.任一输入为

1

二、判断题（正确打√，错误的打×）

1．逻辑变量的取值，１比０大。

（）。

2．异或函数与同或函数在逻辑上互为反函数。

（）。

3．若两个函数具有相同的真值表，则两个逻辑函数必然相等。

（）。

4．因为逻辑表达式A+B+AB=A+B成立，所以AB=0成立。

（）

5．若两个函数具有不同的真值表，则两个逻辑函数必然不相等。

（）

6．若两个函数具有不同的逻辑函数式，则两个逻辑函数必然不相等。

（）

7．逻辑函数两次求反则还原，逻辑函数的对偶式再作对偶变换也还原为它本身。

（）

8．逻辑函数

Y=AB+AB+BC+BC

已是最简与或表达式。

（

）

9．因为逻辑表达式

AB+AB+AB=A+B+AB成立，所以

AB+AB=A+B成立。

（

）

10．对逻辑函数Y=AB+AB+BC+BC利用代入规则，令A=BC代入，得Y=BCB+BCB+BC+BC=BC+BC

成立。

（）

三、填空题

1.

逻辑代数又称为

代数。

最基本的逻辑关系有

、

、

三种。

常用

的几种导出的逻辑运算为

、

、

、

、

。

2.

逻辑函数的常用表示方法有

、

、

。

3.

逻辑代数中与普通代数相似的定律有

、

、

。

摩根定律又称为

。

4.

逻辑代数的三个重要规则是

、

、

。

5

．逻辑函数F=A+B+CD的反函数F=

。

6

．逻辑函数F=A（B+C）·1的对偶函数是

。

7

．添加项公式AB+AC+BC=AB+AC的对偶式为

。

8

．逻辑函数F=ABCD+A+B+C+D=

。

9

．逻辑函数F=ABAB

ABAB=

。

10．已知函数的对偶式为

AB+CDBC，则它的原函数为

。

四、思考题

1.逻辑代数与普通代数有何异同

2.逻辑函数的三种表示方法如何相互转换

3.为什么说逻辑等式都可以用真值表证明

4.对偶规则有什么用处

5．化简逻辑函数表达式的意义是什么什么叫最简的与或表达式

6．公式化简法有什么优点和缺点

7．什么叫最小项最小项有什么性质你能根据逻辑函数的定义说明函数最小项与或表达式的唯一性吗

8．什么叫卡诺图卡诺图上变量取值的排列有什么规律

9．卡诺图中最小项（小方块）合并的规律是什么几何位置上相邻的三、五、六、七、九、十、十五个

最小项（小方块）能够合并在一起吗为什么

10．在卡诺图中约束项一般是怎样处理的为什么

11．在化简具有约束的逻辑函数时，充分利用约束条件有什么好处

12．利用约束条件（或约束项）化简得到的函数表达式成立的先决条件是什么

五、练习题

1.为使F=A，则B应为何值（高电平或低电平）

2.指出图中各TTL门电路的输出是什么状态（高电平、低电平、高阻）

3.指出图中各CMOS门电路的输出是什么状态

4.用公式法将下列函数化为最简与或表达式。

1）Y=AB+C+AC+B

2）Y=AC+BC+BD+CD+A（B+C）+ABCD+ABDE

3）Y=AC+ABC+ACD+CD

4）Y=A（C⊕D）+BCD+ACD+ABCD

5.用卡诺图化简法将函数化为最简与或表达式。

1）Y=BD+ABCD+ABCD+ABCD+ABCD

2）Y（A，B，C，D）=∑（m3,m5,m6,m7,m10）

给定约束条件为m0+m1+m2+m4+m8=0

3）Y=BCD+AB+ACD+ABC

4）Y（A，B，C，D）=∑（m1,m4,m8,m9,m12）

6.根据要求完成下列各题：

（1）用代数法化简函数：

（2）证明下列恒等式：

7.将下图所示电路化简成最简与或表达式。

8.利用卡诺图化简:

9.化简逻辑函数：

10.试利用卡诺图化简下列逻辑函数：

11.设逻辑表达式：

试画出其逻辑图。

12.化简如图所示的电路，要求化简后的电路逻辑功能不变。

13.写出逻辑函数Y2的最简与或表达式，画出最简与非逻辑图。

14.电路如图所示，设开关闭合为1，断开为0，灯亮为1，灯灭为0。

列出反映逻辑L和A、B、

C关系的真值表，并写逻辑函数L的表达式。

15.列出函数的真值表。

16.

（1）证明等式：

AB+C+

C=AB+C

（2）化简函数：

Y1=

17.写出图（a）、图（

∑mn（0,1,3,5,8,9）+∑d（10,11,12,13,14,15）

b）电路的逻辑函数表达式，并将结果化为最简与或表达式的形式。

18.证明等式：

AB+C+

C=AB+C

19.化简函数：

Y1=∑mn（0,1,3,5,8,9）+

∑d（10,11,12,13,14,15）

20.化简。

21.化简逻辑函数：

22.化简下列逻辑函数，写出它们的最简与或表达式。

（1）Z1=A+C+BCD

（2）Z2=

+

BC+A

AB+AC=0

23.用代数法将下列函数化简为最简与或表达式。

（1）

（2）

34.用基本公式和定理证明下列等式：

（1）

（2）F2（A、B、C、D）=（8、9、10、11、12）

+（5、6、7、13、14、15）

25.化简逻辑函数：

26.化简逻辑函数：

27.写出如图所示各逻辑图的逻辑表达式。

28.化简下列逻辑函数，假设约束条件为：

AB+AC=0

（1）F（A、B、C、D）=∑（1、2、3、7、8、9）

（2）F（A、B、C、D）=∑（2、3、4、6、8、9）

29.用卡诺图化简下列函数，并用与非门画出逻辑电路图。

F（A、B、C、D）=（Σ0、2、6、7、8、9、10、13、14、15）

30.

用卡诺图化简函数

。

31.

列出下列各函数的真值表，并说明

y1、y2的关系。

（1）y1=B+

C+Ay2

=A+B+C

（2）y1=

+ABCy2

=

32.用代数法化简下列函数

33.一个三变量逻辑函数的真值表如下表所示，写出其最小项表达式，画出卡诺图并化简之。

ABCF

0000

0011

0100

0110

1001

1011

1100

1110

34.真值表如表所示，试写出逻辑函数表达式。

35.化简下列逻辑函数

L（A，B，C，D）=Σm（0，1，5，6，7，，8，9，，13）+Σd（2，

4，10）

数字电子技术基础习题集

项目一习题

1.将下列二进制数转换为十进制数

（1）10101

（2）（3）

2.写出下列八进制数的按权展开式

（1）（247）8

（2）（）8（3）（）8

3.将下列十六进制数转换为十进制数

（1）（6BD）16

（2）（）16（3）（）16

4.将下列十进制数转换为二进制数，小数部分精确到小数点后第四位

（1）（47）10

（2）（）10（3）（）10

5.将下列二进制数转换为八进制数

（1）（）2

（2）（）2（3）（）2

6.将下列二进制数转换为十六进制数

（1）（11）2

（2）（）2（3）（）2

7.指出下列逻辑函数式中A、B、C取哪些值时，F=1。

（1）F（）=AB+AC

（2）F（A.B.C.）=A+BC（A+B）

（3）F（）=AB+ABC+ABC

8.用公式法化简下列函数，使之为最简与或式。

（1）F=AB+AC+BC+ABCD

（2）F=（A+B）AB

（3）F=AC+ABC+BC+ABC

（4）F=AB（C+D）+BC+AB+AC+BC+BCD

（5）F=（A+BC）（A+DE）

9.直接画出逻辑函数F=AB+B（A⊕C）的实现电路

10.有三个输入信号A、B、C，若三个同时为0或只有两个信号同时为1时，输出F为1，否则F为0。

列出其真值表。

11.用真值表证明下列等式

（1）A+B=A·B

（2）AB+AB=（A+B）（A+B）

12.直接根据对偶规则和反演规则，写出下列逻辑函数的对偶函数和反函数

（1）F=A+BC+A（B+CD）

（3）F=（A+B）（B+C）（A+C）

（2）F=AB+BC+AC

（4）F=AB（C+BC）+A（B+C）

13.判断下列命题是否正确

（1）已知逻辑函数A+B=A+C，则B=C

（2）已知逻辑函数A+B=AB，则A=B

（3）已知逻辑函数AB=AC，则B=C

（4）已知逻辑函数A+B=A+C，AB=AC，则B=C

14.用卡诺图化简下列函数，并写出最简与或表达式

（1）F（）=ABC+ABD+ABC+BD+ABCD

（2）F（）=AC+BC+ABC

（3）F（）=∑m（0，2，3，7）

（4）F（）=∑m（1，2，4，6，10，12，13，14）

（5）F（）=∑m（0，1，4，5，6，7，9，10，13，14，15）

（6）F（）=∑m（0，2，4，7，8，10，12，13）

（7）F（）=∑m（1，3，4，7，13，14）+∑d（2，5，12，15）

（8）F（）=∑m（0，1，12，13，14）+∑d（6，7，15）

（9）F（）=∑m（0，1，4，7，9，10，13）+∑d（2，5，8，12，15）

（10）F（）=∑m（0，2，7，13，15）且ABC+ABD+ABD=0

第一章习题答案

1.

（1）（21）10

（2）（）10（3）（）10

2.

（1）（247）8=2×82+4×81+7×80

（2）（）8=6×81+5×82+1×83

（3）（）8=4×82+6×81+5×80+4×81+3×82

3.

（1）（1725）10

（2）（）10

（3）（）10

4.

（1）（101111）2

（2）（）2

（3）（）2

5.

（1）（275）8

（2）（）8

（3）（）8

6.

（1）（77B）16

（2）（）16

（3）（）16

7.解此题时应把F表达式展开成最小项标准与或式，每个最小项所对应的输入便是问题的答案。

（1）F（）=AB+AC=AB（C+C）+AC（B+B）

=ABC+ABC+ABC+ABC

=m7+m6+m3+m1

当ABC为输入组合111，110，011，001中任一种时，F=1。

（2）F（A.B.C）=A+BC（A+B）=ABC（A+B）

=A（B+C）（A+B）

=（AB+AC）（A+B）

=ABC

当ABC取011时，F=1。

（3）F（）=AB+ABC+ABC

=AB（C+C）+ABC+ABC

=ABC+ABC+ABC

当ABC为输入组合111，011，010中任一种时，F=1。

8．

（1）F=AB+C

（2）F=AB

（3）F=C

（4）F=1

（5）F=AB+AC+AD+AE

9．电路图如下图所示

A＆

B

A

=1

≥1

F

C

＆

B

10.

A

B

C

F

0

0

0

1

0

0

1

0

0

1

0

0

0

1

1

1

1

0

0

0

1

0

1

1

1

1

0

1

1

1

1

0

11.

（1）

令F1=A+B

F2=A·B

A

B

1

2

F

F

0

0

1

1

0

1

0

0

1

0

0

0

1

1

0

0

（2）令F1=AB+ABF2=（A+B）（A+B）

A

B

1

2

F

F

0

0

0

0

0

1

1

1

1

0

1

1

1

1

0

0

12.

（1）F’=A（B+C）[A+B（C+D）]F=A（B+C）[A+B（C+D）]

（2）F’=（A+B）（B+C）（A+C）F=（A+B）（B+C）（A+C）

（3）F’=AB+（BC+AC）F=AB+（BC+AC）

（4）F’=[A+B+C（B+C）]（A+BC）F=[A+B+C（B+C）]（A+BC）

13.

（1）×

（2）√（3）×（4）√

14.

（1）F=AB+AC+BD+BC

（2）F=A+BC

（3）F=BC+AC

（4）F=CD+ABC+BD+ABCD

（5）F=AC+CD+BC+ACD

（6）F=CD+BD+ABC+ABCD

（7）F=BC+AB+AD

（8）F=AB+ABC

（9）F=C+BD+BD

（10）F=A+BD

卡诺图如下

CD

AB

00

01

11

10

00

1

1

1

BC

11

10

01

A

00

01

11

1

1

0

1

10

1

1

1

1

1

1

1

1

1

（1）

（2）

CD

01

1110

AB

00

BC

00

1

1

A

00

01

11

10

01

1

1

0

1

1

1

11

1

1

1

1

1

10

1

（3）

（4）

CD

CD

011110

00

01

11

10

AB

00

AB

00

1

1

00

1

1

01

1

1

1

1

01

1

1

11

1

1

1

11

1

1

10

1

1

10

1

1

（5）

（6）

CD

AB00011110

0011×

011×1

11×1×1

10

（7）

CD

AB00011110

0011×

011×1

11×1×

10×11

（9）

CD

AB

00

01

11

10

00

1

1

01

×

×

11

1

1

×

1

10

（8）

CD

AB00011110

001××1

01××1×

1111

10

（10）