spss数据正态分布检验方法及意义.docx

spss数据正态分布检验方法及意义.docx

《spss数据正态分布检验方法及意义.docx》由会员分享，可在线阅读，更多相关《spss数据正态分布检验方法及意义.docx（31页珍藏版）》请在冰豆网上搜索。

spss数据正态分布检验方法及意义

spss数据正态分布检验方法及意义判读

要观察某一属性的一组数据是否符合正态分布，可以有两种方法（目前我知道这两种，并且这两种方法只是直观观察，不是定量的正态分布检验）：

1：

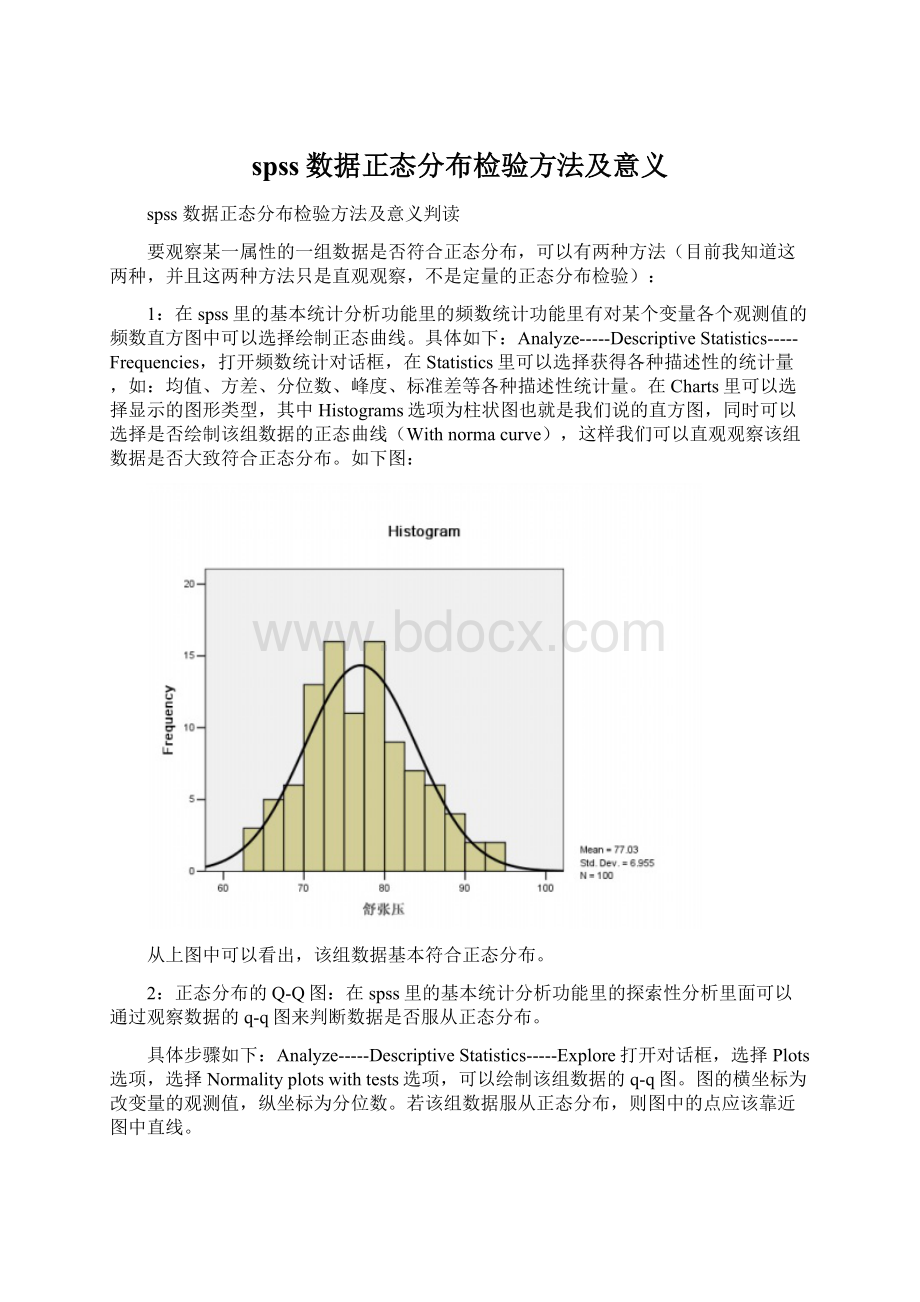
在spss里的基本统计分析功能里的频数统计功能里有对某个变量各个观测值的频数直方图中可以选择绘制正态曲线。

具体如下：

Analyze-----DescriptiveStatistics-----Frequencies，打开频数统计对话框，在Statistics里可以选择获得各种描述性的统计量，如：

均值、方差、分位数、峰度、标准差等各种描述性统计量。

在Charts里可以选择显示的图形类型，其中Histograms选项为柱状图也就是我们说的直方图，同时可以选择是否绘制该组数据的正态曲线（Withnormacurve），这样我们可以直观观察该组数据是否大致符合正态分布。

如下图：

从上图中可以看出，该组数据基本符合正态分布。

2：

正态分布的Q-Q图：

在spss里的基本统计分析功能里的探索性分析里面可以通过观察数据的q-q图来判断数据是否服从正态分布。

具体步骤如下：

Analyze-----DescriptiveStatistics-----Explore打开对话框，选择Plots选项，选择Normalityplotswithtests选项，可以绘制该组数据的q-q图。

图的横坐标为改变量的观测值，纵坐标为分位数。

若该组数据服从正态分布，则图中的点应该靠近图中直线。

纵坐标为分位数，是根据分布函数公式F（x）=i/n+1得出的.i为把一组数从小到大排序后第i个数据的位置，n为样本容量。

若该数组服从正态分布则其q-q图应该与理论的q-q图（也就是图中的直线）基本符合。

对于理论的标准正态分布，其q-q图为y=x直线。

非标准正态分布的斜率为样本标准差，截距为样本均值。

如下图：

如何在spss中进行正态分布检验1（转）（2009-07-2211:

11:

57）

标签：

杂谈 

一、图示法

1、P-P图

以样本的累计频率作为横坐标，以安装正态分布计算的相应累计概率作为纵坐标，把样本值表现为直角坐标系中的散点。

如果资料服从整体分布，则样本点应围绕第一象限的对角线分布。

2、Q-Q图

以样本的分位数作为横坐标，以按照正态分布计算的相应分位点作为纵坐标，把样本表现为指教坐标系的散点。

如果资料服从正态分布，则样本点应该呈一条围绕第一象限对角线的直线。

以上两种方法以Q-Q图为佳，效率较高。

3、直方图

判断方法：

是否以钟形分布，同时可以选择输出正态性曲线。

4、箱式图

判断方法：

观测离群值和中位数。

5、茎叶图

类似与直方图，但实质不同。

二、计算法

1、偏度系数（Skewness）和峰度系数（Kurtosis）

计算公式：

g1表示偏度，g2表示峰度，通过计算g1和g2及其标准误σg1及σg2然后作U检验。

两种检验同时得出U0.05的结论时，才可以认为该组资料服从正态分布。

由公式可见，部分文献中所说的“偏度和峰度都接近0……可以认为……近似服从正态分布”并不严谨。

2、非参数检验方法

非参数检验方法包括Kolmogorov-Smirnov检验（D检验）和Shapiro-Wilk（W检验）。

SAS中规定：

当样本含量n≤2000时，结果以Shapiro–Wilk（W检验）为准，当样本含量n>2000时，结果以Kolmogorov–Smirnov（D检验）为准。

SPSS中则这样规定：

（1）如果指定的是非整数权重，则在加权样本大小位于3和50之间时，计算Shapiro-Wilk统计量。

对于无权重或整数权重，在加权样本大小位于3和5000之间时，计算该统计量。

由此可见，部分SPSS教材里面关于“Shapiro–Wilk适用于样本量3-50之间的数据”的说法是在是理解片面，误人子弟。

（2）单样本Kolmogorov-Smirnov检验可用于检验变量（例如income）是否为正态分布。

对于此两种检验，如果P值大于0.05，表明资料服从正态分布。

三、SPSS操作示例

SPSS中有很多操作可以进行正态检验，在此只介绍最主要和最全面最方便的操作：

1、工具栏--分析—描述性统计—探索性

2、选择要分析的变量，选入因变量框内，然后点选图表，设置输出茎叶图和直方图，选择输出正态性检验图表，注意显示（Display）要选择双项（Both）。

3、Output结果

（1）Descriptives：

描述中有峰度系数和偏度系数，根据上述判断标准，数据不符合正态分布。

Sk=0，Ku=0时，分布呈正态，Sk>0时，分布呈正偏态，Sk<0时，分布呈负偏态，时，Ku>0曲线比较陡峭，Ku<0时曲线比较平坦。

由此可判断本数据分布为正偏态（朝左偏），较陡峭。

（2）TestsofNormality：

D检验和W检验均显示数据不服从正态分布，当然在此，数据样本量为1000，应以W检验为准。

（3）直方图

直方图验证了上述检验结果。

（4）此外还有茎叶图、P-P图、Q-Q图、箱式图等输出结果，不再赘述。

结果同样验证数据不符合正态分布。

spss 判断两组数据的相关性（已使用）（2009-07-2213:

07:

34）

标签：

杂谈 

两组体重数据：

先要为数据分组

2.0 3000.0

2.0 3700.0

2.0 2900.0

2.0 3200.0

2.0 2950.0

2.0 3100.0

2.0 700.0

2.0 3200.0

2.0 2500.0

2.0 3650.0

2.0 3450.0

2.0 4600.0

2.0 2700.0

2.0 2500.0

2.0 3150.0

2.0 3500.0

2.0 3800.0

2.0 2800.0

2.0 2400.0

2.0 3600.0

2.0 3200.0

2.0 1770.0

2.0 1450.0

2.0 1700.0

2.0 3250.0

2.0 2700.0

2.0 3000.0

2.0 2250.0

2.0 2150.0

2.0 2450.0

2.0 1600.0

2.0 3100.0

2.0 4050.0

2.0 4250.0

2.0 2900.0

2.0 3250.0

2.0 3750.0

2.0 3500.0

2.0 4100.0

2.0 3100.0

2.0 2400.0

2.0 3250.0

2.0 2600.0

2.0 3100.0

2.0 3400.0

1.0 2400.0

1.0 2100.0

1.0 3000.0

1.0 2600.0

1.0 4000.0

1.0 2200.0

1.0 1400.0

1.0 3000.0

1.0 3200.0

1.0 3600.0

1.0 2850.0

1.0 2850.0

1.0 3300.0

1.0 3500.0

1.0 3900.0

1.0 3250.0

1.0 3800.0

1.0 2800.0

1.0 3500.0

1.0 2650.0

1.0 2350.0

1.0 1400.0

1.0 2900.0

1.0 2550.0

1.0 2850.0

1.0 3300.0

1.0 2250.0

1.0 2500.0

使用命令：

spss的t检验：

菜单Analyze->CompareMeans->Independent-SamplesTTest

运行结果：

经方差齐性检验：

F=0.393  P=0.532，即两方差齐。

（因为p大于0.05）

所以选用t检验的第一行方差齐情况下的t检验的结果：

就是选用方差假设奇的结果

 所以，t=0.644 ,   p=0.522,没有显著性差异。

（因为 p<0.05表示差异有显著性）。

均值相差：

113.30159    

解释：

使用comparemeans里的independentsmaplesTtest,检验结果里的Levene\'sTestforEqualityofVariances就是对方差齐性的检验,如果P值大于0.05则认为是方差齐,统计量为F=S1^2/S^2~F（n1-1,n2-1）,显著水平一般为0.05,0.01,原假设H0:

方差相等。

方差分析（AnaylsisofVariance,ANOVA）要求各组方差整齐，不过一般认为，如果各组人数相若，就算未能通过方差整齐检验，问题也不大。

One-WayANOVA对话方块中，点击Options…（选项…）按扭，

勾Homogeneity-of-variance即可。

它会产生

Levene、CochranC、Bartlett-BoxF等检验值及其显著性水平P值，

若P值<于0.05，便拒绝方差整齐的假设。

顺带一提，Cochran和Bartlett检定对非正态性相当敏感，

若出现「拒绝方差整齐」的检测结果，或因这原因而做成。

 Statistics菜单->CompareMeans->Independent-samplesTTest..

再看看结果中p值的大小是否<.05，若然即达显著水平。

SPSS学习笔记

描述样本数据

一般的，一组数据拿出来，需要先有一个整体认识。

除了我们平时最常用的集中趋势外，还需要一些离散趋势的数据。

这方面EXCEL就能一次性的给全了数据，但对于SPSS，就需要用多个工具了，感觉上表格方面不如EXCEL好用。

个人感觉，通过描述需要了解整体数据的集中趋势和离散趋势，再借用各种图观察数据的分布形态。

对于SPSS提供的OLAPcubes（在线分析处理表），CaseSummary（观察值摘要分析表），Descriptives（描述统计）不太常用，反喜欢用Frequencies（频率分析），BasicTable（基本报表），Crosstabs（列联表）这三个，另外再配合其它图来观察。

这个可以根据个人喜好来选择。

一．使用频率分析（Frequencies）观察数值的分布。

频率分布图与分析数据结合起来，可以更清楚的看到数据分布的整体情况。

以自带文件Trendschapter13.sav为例，选择Analyze->DescriptiveStatistics->Frequencies，把hstarts选入Variables，取消在DisplayFrequencytable前的勾，在Chart里面histogram，在Statistics选项中如图1

图1

分别选好均数（Mean），中位数（Median），众数（Mode），总数（Sum），标准差（Std.deviation），方差（Variance），范围（range），最小值（Minimum），最大值（Maximum），偏度系数（Skewness），峰度系数（Kutosis），按Continue返回，再按OK，出现结果如图2

图2

表中，中位数与平均数接近，与众数相差不大，分布良好。

标准差大，即数据间的变化差异还还小。

峰度和偏度都接近0，则数据基本接近于正态分布。

下面图3的频率分布图就更直观的观察到这样的情况

图3

二．采用各种图直观观察数据分布情况，如采用柱型图观察归类的比例等。

同样以自带文件Trendschapter13.sav为例，我们可以观察一下各年的数据总和的对比：

1．选择Graph->Bar->Simple，在“Datainchartare”一项选择Summaryofgroupsofcases，然后按Define，出现图4，

图4

2．选择BarsRepresent->Otherstatistic（e.g.mean），把hstarts一项选入Variable里面，把YEAR,Periodic一项选入CategoryAxis项中，并按ChangeStatistic键，出现图5：

图5

3．在Statistic选项中选Sumofvalues一项，按Continue返回，按OK即可出现图6：

图6

从图中可以非常直观的看出1965年-1975年间，每年的总体数量对比和各数值多少。

三．通过列联表来观察，数据的交错关系。

以软件自带的文件UniversityofFloridagraduatesalaries.sav来说明

1、选择Tables->BasicTable，在弹出对话框中，选择Graduate到Summaries栏，College到Down，Gender到Across栏，如图7

图7

2、选择Statistics按键，选取Count和layer%到CellStatistics一栏，并按Continue键，如图8

图8

三、选择Layout按键，选择SummaryVariableLabels->Inseparatelabels（汇总的标签，如本例的Graduate，放在表外），StatisticsLabels->Acrosstop（数据的标签横放在顶部，如本例的Count和Layer%），并在Labelgroupswithvaluelabelsonly前选择打勾（表示只需要具体的标签名就可以，不需要汇总名，如本例Gender和College），如图9

图9

四、选择Total按键，在Totalsovereachgroupvariable一项前选勾，则输出表会有增加汇总一栏，如图10

图10

提示，需要什么表格形式可以根据要求来调整，但对输出按键都需要熟悉，多尝试几次就可以看出不同的区别。

图11为输出的表格

图11

重要提示：

如果结果变成变量的汇总（SUM），则先选择Data->WeightCases，把Graduate的选项先选入WeightCasesby内，再选回DonotweightCases，按OK即可。

对于其他带有编号的一项都可以这样做。

这一点不知为何，本人屡次试过总需要这样调整。

参考图12

图12

几种常用的统计方法应用

一般来说，最最常用的统计分析有假设检验和回归分析，在SPSS中也有很好的对应工具来做这些分析，但对其基本思路和要求都必须了解，这样才能更灵活的发挥。

下面抄录《EXCEL在市场调查中的应用》一书中关于这方面的内容：

1．假设检验

目的：

是用来判断样本与样本，样本与总体的差异是由抽样误差引起还是本质差别造成的统计推断方法。

基本思想：

小概率反证法思想。

即P<0.01或P<0.05在一次试验中基本不会生发。

反证法思想是先提出假设（检验假设H0），再用适当的统计方法确定假设成立的可能性大小，如果可能性小，则认为假设不成立，否则，还不能认为假设不成立。

方法：

t检验，u检验，秩和检验，卡方检验

应用条件：

A、各组资料具有可比性

B、具正态分布

C、方差齐性（即先作F检验，如F0.1，具方差齐性）

2．方差分析

目的：

又称为变异系数分析或F检验。

用于推断两组或多组资料的总体平均数是否相同，检验两个或多个样本平均数的差异是否具有统计意义（也可认为是检验多个总体均值是否有显著性差异注1，这样可能更简单一点）。

基本思想：

用组内均方去除组间均方的商，即F值，与1比较，若F值接近1，则说明各验均数间的差异没有统计学意义，否则表示有统计学意义。

应用条件：

A、各组资料具有可比性

B、具正态分布

C、方差齐性（即F检验）

提示，在应用SPSS中，只要死死的记住一个显著系数0.05就可以应用（如果是双尾系数需要除以2），一般的大于0.05接受原假设，小于0.05则拒绝。

简单的说，一般结果拒绝就是说样本有差异，样本相对独立，都是表示同一种意思，读这方面书的时候，希望不要让这些名词混乱了思路。

SPSS的方差检验中，需要注意下面问题：

方差检验中，PostHoc键有LSD的选项：

当方差分析F检验否定了原假设，即认为至少有两个总体的均值存在显著性差异时，须进一步确定是哪两个或哪几个均值显著地不同，则需要进行多重比较来检验。

LSD即是一种多因变量的三个或三个以上水平下均值之间进行的两两比较检验。

2IndependentSamples检验中的Mann-WhitneyU检验与KIndependentSamples中的Kruskal-Walllis（克鲁斯卡尔—瓦里斯）H检验法思想类似，常用来作为非参数检验。

2RelatedSamples非参数检验中，一般有Sign普通符号检验法和Wilcoxon威尔科克森符号秩检验法。

前者用于研究的问题只有两个可能的结果：

“是”或“非”，并且二者遵从二项分布；后者是普通符号检验法的改进，除了可以检验是非外，还可以了解差异的大小。

KRelatedSamples非参数检验中，主要有Friedman秩和检验与CochranQ检验二种选择，前者是对多个样本是否来自同一总体的检验，而后者是用于只分为“成功”和“失败”两种结果的定类尺度测量的数据。

附录：

SPSS假设检验方法使用对照表

图13

其中相关、配对或有交互作用可以理解为EXCEL的重复，独立或无交互作用可以理解为EXCEL中的无重复。

图13表大部分参考《数据分析与SPSS应用》一书，特别说明

3．回归分析

目的：

研究一个变量Y与其它若干变量X之间的一种数学工具。

它是一组试验或观测数据的基础上，寻找被随机性掩盖的变量之间的依存关系。

A．直线回归方程Yc=abX

B．回归关系的检验：

求回归方程在总体中是否成立，即是否样本代表的总体也有直线回归关系。

a.方差分析：

基本思想是将总变异分解为SS回归和SS乘余，然后利用F检验来判断方程是否成立。

b.t检验：

基本思想是利用样本回归系数b与总体平均数回归系数进行比较来判断回归方程是否成立。

下面摘录《数据分析与SPSS应用》一书关于相关回归和时间序列分析一些概念解释。

数据变量间主要存在二类关系：

一类是函数关系，一类是相关关系。

前者是变量间有确定关系，即一个变量的值能够在其他变量取值确定的情况下，按某种函数关系唯一确定；后者是变量间虽然具有的联系，并非确定关系，如价格与销量量，价格高了，销售量可能会上去，但无法确定销售量是多少。

通过散点图来观察，如果点都集中在一条直线附近，是线性相关，如果在一条曲线附近，则为非线性相关。

如果一个变量因另一个变量的增加而增加，减少而减少，则二个变量间存在正相关关系，反之则为负相关关系。

极端的相关是完全相关和零相关。

如某地区购买自行车多少与购买大蒜多少无关，是为零相关。

按我的理解，相关分析就是推断变量与变量之间关系的密切程度，回归就是在相关的基础上，找出变量间的拟合模型，从而进一步推测出未来的趋势和变量。

而时间序列则是以时间的作为观察的序列，来推断变量间的关系的一种模型。

以自带文件Trendschapter13.sav为例，说明一下如何应用这三种分析工具。

1．相关

打开Trendschapter13.sav文件，可以看到，这个文件的数据是以时间来排序的，在每个值前增加一行序列号变量，如图14

图14

一个时间序列的影响因素有四种变动：

A长期趋势（SecularTrend），B季节变动（SeasonalVariation），C循环变动（CyclicalVariation），D不规则变动（IrregularVariation）。

我们可以观察一下这些数据是否存在某种关系，打开Graphs->Sequence，如图15

图15

把hstarts选入Variables项，把No.选入TimeAxisLables，然后按OK，出现图16：

图16

从图可以看出，数据总是在一个周期内反复在上下波动，虽然高低的位置不一样，但这种波动显然是随着时间的不同而变化。

因此可以察看，因变量与时间的关系如何。

选择Data->DefineDates，出现图17

图17

在Year一栏填入1965，Month一栏填入1，表示数据从1965年1月开始计算。

选择Analyze->Correlate->Bivariate，出现图18

图18

把hstarts，Year和Month都选入Varibales选项，CorrelationCoefficients选择Pearson和Spearman（其实只需要选Spearman就可以，这里只是试一下，作为比较）。

注：

相关检验中有Pearson（皮尔森）相关系数和Spearman（斯皮尔曼）等级相关，前者也称皮尔森相关系数，是对两个定距变量关系的刻画；后者是用来考察两个变量中至少有一个定序变量时的相关关系。

Zero-orderCorrelations（零阶偏听偏相关系数）是按Pearson简单相关系数公式计算得到的相关系数。

在皮尔森系数r是对两个定距变量关系的刻画:

若-1≤r≤1，|r|越大，表明两个变量之间的相关程度越强。

若0

若r=1，则表明变量之间存在着完全正相关的关系。

若-1≤r<0，表明两个变量之间存在负相关。

若r=-1，则变量间的关系为完全负相关。

若r=0，表示两个变量之间无线性相关，即零相关。

按Option按键，如图19

图19

在Statistics选择MeansandstandarddeviationsCross-productdeviationsandcovariances，注意，这二个选择是Pearson才有的，如果开始只选择Spearman，则此二项不能选。

返回后，按OK如图20：

图20

从图20看到Year的Pearson系数为0.219，Sig值为0.012，小于P值0.05，与Hstarts显著相关，Month的Pearson系数为0.058，Sig值为0.506，大于P值0.05，则与Hstarts不显著相关。

从下图21的Spearman也同样得到相同的结论。

图21

2．回归

试建立回归模型，看能否形成各变量间的关系式。

选择Analyze->Regression->CurveEstimation，出现图22

图22

把hatarts选入Dependents选项，Independent选择Time，Models选择（Linear）线性回归，（Quadratic）二次曲线回归，（Cubic）三次曲线回归，（Exponential）指数回归，选择Includeconstantinequation表示方程式有常数项，Plotmodels则表示用图表示，然后按OK，出现图23

图23

线性方程：

Y=70.430.135X

二次曲线方程：

Y=64.1710.415X-0.02X2

三次曲线方程：

Y=87.68-1.667X0.037X2（0X3）

指数曲线方程：

Y=68.229xe0.002

从Sig值判断，都小于0.05，都接受回归成立，这样，只能从R拟合度和F值较大来判断三次曲线方程的拟合程度比较高。

注意，如果方程成立的话，想要增加预测，则可以在Save选项中选择PredictedValues一项，如果还想预测未来的数值，则可以在原表上增加若干行（如1行），然后选择PredictCases下面Predictthrough，在Year填入1976，在Mont