书签分享收藏举报版权申诉 / 17

立即下载加入VIP,免费下载

当前位置：首页 > 高中教育 > 高考 > 运筹学胡运权部分课后习题答案.docx

运筹学胡运权部分课后习题答案.docx

文档编号：7976343
上传时间：2023-01-27
格式：DOCX
页数：17
大小：130.94KB

运筹学胡运权部分课后习题答案.docx

《运筹学胡运权部分课后习题答案.docx》由会员分享，可在线阅读，更多相关《运筹学胡运权部分课后习题答案.docx（17页珍藏版）》请在冰豆网上搜索。

运筹学胡运权部分课后习题答案.docx

运筹学胡运权部分课后习题答案

第一章

P43-1.1

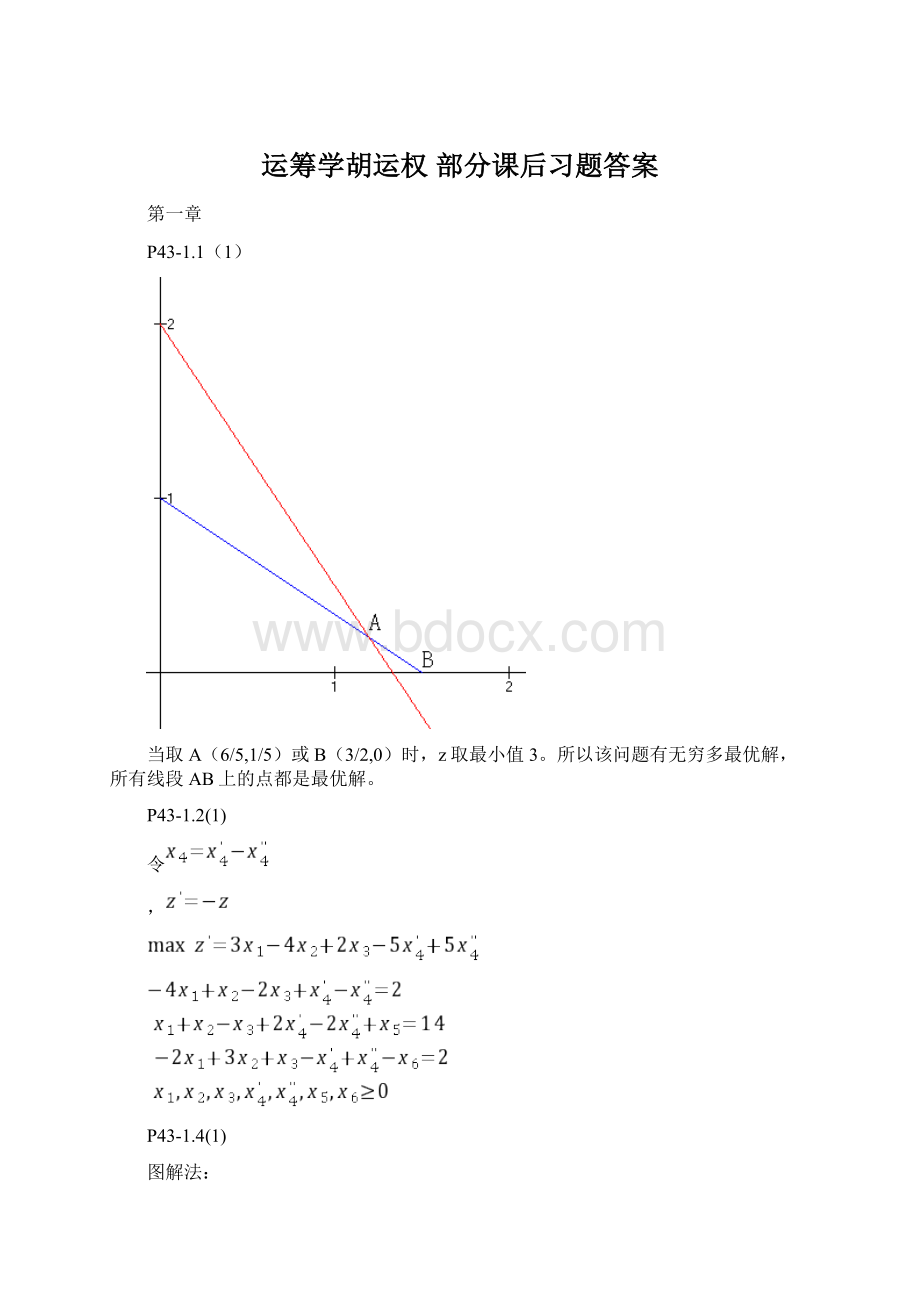
（1）

当取A（6/5,1/5）或B（3/2,0）时，z取最小值3。

所以该问题有无穷多最优解，所有线段AB上的点都是最优解。

P43-1.2

（1）

令

，

P43-1.4

（1）

图解法：

A（0,9/4），Z1=45/4；B（1,3/2），Z2=35/2；C（8/5,0），Z3=16。

单纯形法：

10

5

0

Cb

Xb

b

x1

x2

x3

x4

θ

0

x3

9

3

4

1

0

3

0

x4

8

5

2

0

1

8/5

δ

10

5

0

x3

21/5

0

14/5

1

-3/5

3/2

10

x1

8/5

1

2/5

0

1/5

4

δ

0

1

0

-2

5

x2

3/2

0

1

5/14

-3/14

10

x1

1

0

-1/7

2/7

δ

0

-5/14

-25/14

依次相当于：

原点；C；B。

P44-1.7

（1）

大M法：

2

-1

2

0

-M

Cb　

Xb　

b　

x1

x2

x3

x4

x5

x6

x7

x8

x9

θ

-M

x7

6

1

-1

0

1

0

6　

-M

x8

2

-2

0

1

0

-1

0

1

0

-　

-M

x9

0

2

-1

0

-1

0

1

0　

δ

-M+2　

3M-1　

M+2　

-M　

0　

-M

x7

6

1

0

3/2

-1

0

1/2

1

0

-1/2

4

-M

x8

2

-2

0

1

0

-1

0

1

0

2

-1

x2

0

1

-1/2

0

-1/2

0

1/2

δ

-M+

0

2.5M+

-M　

0.5M-

0

-1.5M+

-M

x7

3

4

0

-1

3/2

1/2

1

-3/2

-1/2

2

x3

2

-2

0

1

0

-1

0

1

0

-1

x2

1

-1

1

0

-1/2

0

1/2

δ

4M+5

0

-M

1.5M+

0.5M-

0

-2.5M-

-1.5M+

2

x1

3/4

1

0

-1/4

3/8

1/8

1/4

-3/8

-1/8

2

x3

7/2

0

1

-1/2

-1/4

1/4

1/2

1/4

-1/4

-1

x2

7/4

0

1

0

-1/4

-1/8

-3/8

1/4

1/8

3/8

δ

0

5/4

-3/8

-9/8

-M-

-M+

无界解。

两阶段法：

阶段一：

0

-1

Cb　

Xb　

b　

x1

x2

x3

x4

x5

x6

x7

x8

x9

θ

-1

x7

6

1

-1

0

1

0

6

-1

x8

2

-2

0

1

0

-1

0

1

0

-

-1

x9

0

2

-1

0

-1

0

1

0

δ

-1

3

1

-1

0　

-1

x7

6

1

0

3/2

-1

0

1/2

1

0

-1/2

4

-1

x8

2

-2

0

1

0

-1

0

1

0

2

0

x2

0

1

-1/2

0

-1/2

0

1/2

δ

-1

0

5/2

-1

1/2

0

-3/2

-1

x7

3

4

0

-1

3/2

1/2

1

-3/2

-1/2

0

x3

2

-2

0

1

0

-1

0

1

0

x2

1

-1

1

0

-1/2

0

1/2

δ

4

0

-1

3/2

1/2

0

-5/2

-3/2

0

x1

3/4

1

0

-1/4

3/8

1/8

1/4

-3/8

-1/8

0

x3

7/2

0

1

-1/2

-1/4

1/4

1/2

1/4

-1/4

0

x2

7/4

0

1

0

-1/4

-1/8

-3/8

1/4

1/8

3/8

δ

0

-1

阶段二：

2

-1

2

0

Cb　

Xb　

b　

x1

x2

x3

x4

x5

x6

θ

2

x1

3/4

1

0

-1/4

3/8

1/8

2

x3

7/2

0

1

-1/2

-1/4

1/4

-1

x2

7/4

0

1

0

-1/4

-1/8

-3/8

δ

0

5/4

-3/8

-9/8

无界解。

P45-1.10

证明：

CX（0）>=CX*，C*X*>=C*X（0）èCX（0）-CX*+C*X*-C*X（0）>=0，即（C*-C）（X*-X（0））>=0。

P45-1.13

设饲料i使用xi（kg），则

s.t.

第二章

P74-2.1

（1）

P75-2.4

（1）

（2）（8/5,1/5）

（3）无穷多最优解。

P75-2.5

（1）

（2）（0,1,0）是对偶问题一个可行解，对应w=1。

所以z<=1。

P75-2.6

对偶问题：

由于

，则

必不能满足，所以对偶问题无解，原问题无可行解或者有无界解。

而（0,1,1）显然是原问题的解，即原问题有可行解，所以原问题有无界解。

P76-2.9

-4

-12

-18

0

x1

x2

x3

x4

x5

-18

x3

1

1/3

0

1

-1/3

0

-12

x2

3/2

-1/3

1

0

1/3

-1/2

δ

-2

0

-2

-6

P77-2.11

2

-1

1

0

x1

x2

x3

x4

x5

2

x1

6

1

0

x5

10

0

3

1

δ

0

-3

-1

-2

0

（1）

2

3

1

0

x1

x2

x3

x4

x5

2

x1

8/3

1

0

2/3

-1/3

3

x2

10/3

0

1

1/3

δ

0

-4/3

-7/3

-1/3

（2）

2

-1

1

0

x1

x2

x3

x4

x5

2

x1

3

1

0

x5

7

0

3

1

δ

0

-3

-1

-2

0

（3）

2

-1

1

0

x1

x2

x3

x4

x5

x6

2

x1

10/3

1

2/3

0

2/3

0

1/3

0

x5

22/3

0

8/3

0

2/3

1

1/3

1

x3

8/3

0

1/3

1

1/3

0

-1/3

δ

0

-8/3

0

-5/3

0

-1/3

第三章

P104-3.7

最小元素

B1

B2

B3

B4

产量

A1

5

3

8

A2

5

3

8

A3

1

3

4

销量

6

5

6

3

西北角

B1

B2

B3

B4

产量

A1

6

2

8

A2

3

5

8

A3

1

3

4

销量

6

5

6

3

沃格尔

B1

B2

B3

B4

产量

A1

5

3

8

A2

6

2

8

A3

3

1

4

销量

6

5

6

3

最优

P104-3.8

1

2

3

4

5（虚拟列）

生产量

1

12

12.1

12.2

12.3

12.4

25

2

M

11

11.1

11.2

11.3

35

3

M

11.5

11.6

11.7

30

4

M

12.5

12.6

20

交货量

15

20

25

20

30

P104-3.10

（1）

b1

b2

b3

b4

a1

4

5

3

6

0

a2

8

0

1

2

1

a3

2

5

3

1

0

1

4

0

（2）

b1

b2

b3

b4

a1

4

3

5

6

a2

8

2

1

0

a3

2

5

1

3

P104-3.11

1

1'

2

3

3'

Ⅰ

15

18

22

400

Ⅱ

21

25

16

450

Ⅲ

M

0

M

0

70

290

30

250

270

80

第四章

P120-4.2

（1）X=（55,40）

P120-4.3

（1）

0

P1

P2

3P4

P3

5P4

x1

x2

d1-

d1+

d2-

d2+

d3-

d3+

0

x2

300

0

1

-1

-0.2

0.2

0

x1

500

1

0

0.2

-0.2

0

P3

d3-

500

0

-3

3

0.6

-0.6

1

-1

P1

1

P2

1

P3

3

-3

-0.6

0.6

1

P4

3

5

P121-4.5

第五章

P148-5.4

设x1~x8表示队员1~8是否被选中，“1”为选中，“0”为未选中。

P149-5.6

（1）

1

0

Cb

Xb

b

x1

x2

x3

x4

1

x1

5/3

1

0

5/6

-1/6

1

x2

8/3

0

1

-2/3

1/3

Delta

0

-1/6

割平面方程1：

1

0

Cb

Xb

b

x1

x2

x3

x4

x5

1

x1

1

0

-1

1

x2

16/5

0

1

0

1

-4/5

0

x3

4/5

0

1

-6/5

Delta

0

-1/5

割平面方程2：

1

0

Cb

Xb

b

x1

x2

x3

x4

x5

x6

1

x1

0

1

0

-1

0

5/4

1

x2

4

0

1

0

1

0

-1

0

x3

2

0

1

0

-3/2

0

x5

1

0

1

-5/4

Delta

0

-1/4

X*=（0,4），（2,2）。

Z*=4。

P149-5.7

（1）

再以x1<=3和x1>=4分支。

x1>=4无可行解；x1<=3得X=（3,1），z=7为最优解。

P149-5.8

（2）

x1

x2

x3

z

a

b

c

d

过滤

0

T

z>=0

0

1

-1

0

1

0

1

F

0

1

0

F

1

0

2

T

z>=2

1

0

1

0

3

F

1

2

F

X*=（1,0,0），z*=2。

P150-5.12

1.3

0.8

0

1.0

0

1.2

1.3

0

1.0

0

1.2

0

1.05

0

0.2

1.4

1.0

0.9

0.6

0

1.1

0.1

0.6

1.4

0.4

1.4

0.2

0.1

1.4

0.4

1.4

0.2

1.4

0.35

1.4

1.2

0

0.4

0.5

0.8

1.4

0.3

0

0.4

1.3

0.4

1.3

0

1.4

0.2

1.1

1.2

0

1.3

0.15

1.3

1.1

0

0.4

1

0

x11=x23=x34=x45=x52=1，z=1.3+1.3+1.2+1.4+0.9=6.1。

第七章

P227-7.1

A—B3—C3—D1—E，最短距离为11。

P230-7.9（3）

阶段：

k

状态变量：

sk+1表示阶段1-k的总投入

决策变量：

xk表示k阶段投入

状态转移：

sk=sk+1-akxk

阶段指标：

g1（x1）=4x1；g2（x2）=9x2；g3（x3）=2x32

边界：

f0（s1）=0；s4=10

最优指标：

fk（sk+1）=max{gk（xk）+fk-1（sk）}

k=1，

f1（s2）=max{4x1}（0=<2x1<=s2），当x1=s2/2时，f1（s2）=2s2；

k=2，

f2（s3）=max{9x2+2s2}（0=<4x2<=s3）=max{x2+2s3}，当x2=s3/4时，f2（s3）=9s3/4；

k=3，

f3（10）=max{2x32+9s3/4}（0=<3x3<=10）=max{2x32-27x3/4+45/2}，当x3=0时，f3（10）=45/2。

P230-7.11

k=1，f1（s2）=max{80x1}（0=<2x1<=s2）=80[s2/2]

s2

0

1

2

3

4

5

6

f1（s2）

0

80

160

240

x1*

0

1

2

3

k=2，f2（s3）=max{130x2+f1（s2）}

s3

0

1

2

3

4

5

6

x2

0

1

0

1

0

1

0

1

2

c2+f2

0

80

130

160

130

160

210

240

210

260

f2（s3）

0

80

130

160

210

260

x2*

0

1

0

1

2

k=3，f3（6）=max{180x3+f2（s3）}=max{f2（6）,180+f2

（2）}=260，其中x3*=0。

相应的x2*=2，x1*=0。

P231-7.15

k=4，

f4（s4）=max{r4（s4）-u4（s4）,r4（0）-u4（0）-c4（s4）}，s4可取1,2,3。

则：

f4

（1）=15.5，K；f4

（2）=13.5，KR；f4（3）=13，R。

k=3，

f3（s3）=max{r3（s3）-u3（s3）+f4（s3+1）,r3（0）-u3（0）-c3（s3）+f4

（1）}，s3可取1,2。

则：

f3

（1）=29.5，R；f3

（2）=29，R。

k=2，

f2（s2）=max{r2（s2）-u2（s2）+f3（s2+1）,r2（0）-u2（0）-c2（s2）+f3

（1）}，s2只能取1。

则：

f2

（1）=44.5，K。

k=1，

f1（s1）=max{r1（s1）-u1（s1）+f2（s1+1）,r1（0）-u1（0）-c1（s1）+f2

（1）}，s1只能取0。

则：

f1（0）=62.5，K。

所以4年分别保留、保留、更新、保留，最终盈利62.5。

文档加载中……请稍候！
如果长时间未打开，您也可以点击刷新试试。

下载文档到电脑，查找使用更方便

下载	加入VIP,免费下载

版权申诉 word格式文档无特别注明外均可编辑修改；预览文档经过压缩，下载后原文更清晰！ 立即下载

配套讲稿：: 如PPT文件的首页显示word图标，表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
特殊限制：: 部分文档作品中含有的国旗、国徽等图片，仅作为作品整体效果示例展示，禁止商用。设计者仅对作品中独创性部分享有著作权。
关键词：: 运筹学胡运权部分课后习题答案运筹学胡运权部分课后习题答案

冰豆网所有资源均是用户自行上传分享，仅供网友学习交流，未经上传用户书面授权，请勿作他用。

关于本文

本文标题：运筹学胡运权部分课后习题答案.docx
链接地址：https://www.bdocx.com/doc/7976343.html

运筹学胡运权 部分课后习题答案.docx

热门标签

运筹学胡运权部分课后习题答案.docx