QC七大手法之示意图.docx

QC七大手法之示意图.docx

《QC七大手法之示意图.docx》由会员分享，可在线阅读，更多相关《QC七大手法之示意图.docx（28页珍藏版）》请在冰豆网上搜索。

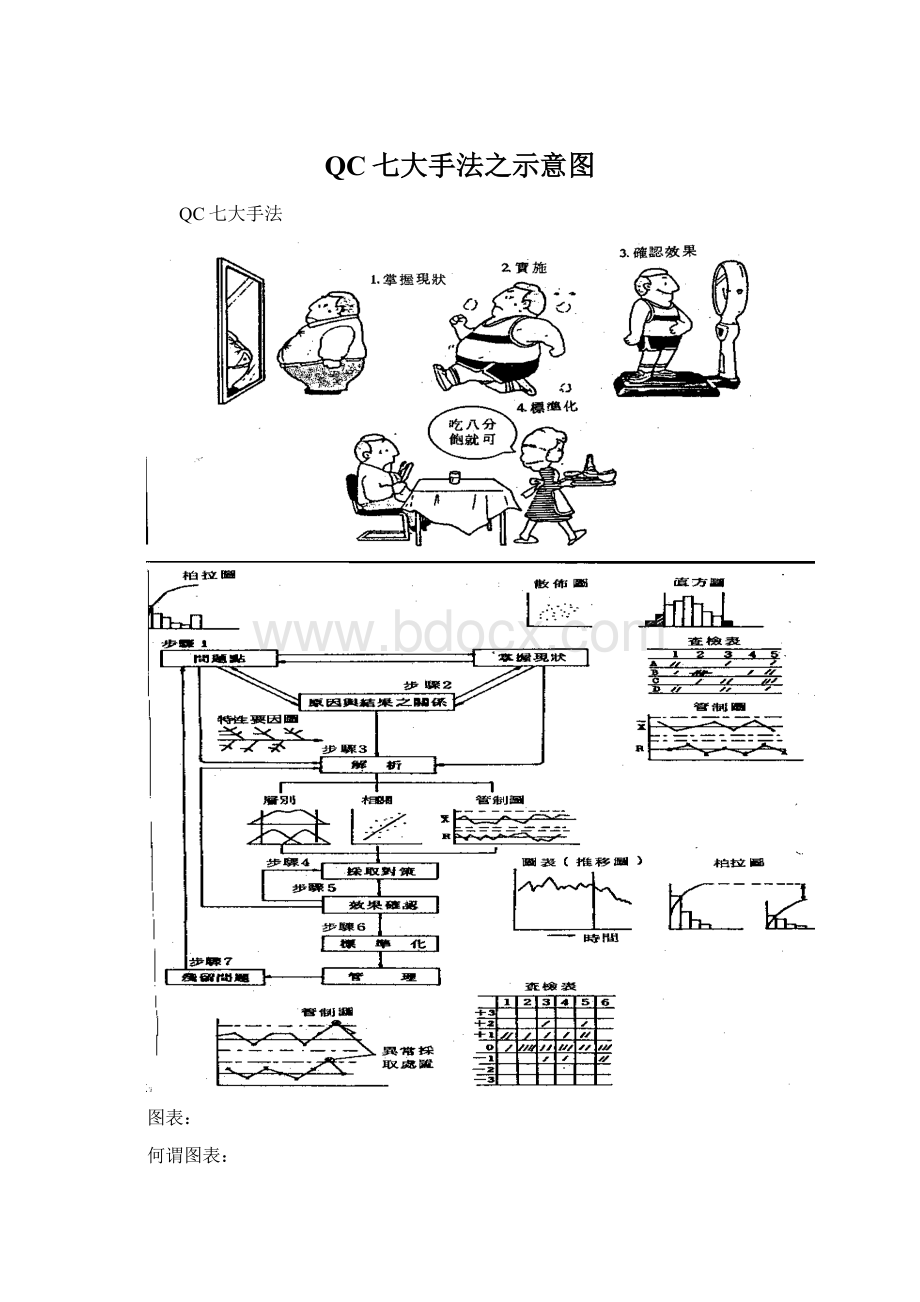
QC七大手法之示意图

QC七大手法

图表：

何谓图表：

现场的数据或情报，用点、线、面、体表示大概情势及钜细变动于纸上的图形，称为图表。

目的为：

（1）方便人的视觉，使其能包括更多的情报，并能传达得更迅速及更易被了解，更快看出情报内容。

（2）自一组数据，能把握到更多的情报，而能采取必要的对策。

图表之功用与具备条件

1.图表之功用

（1）利于多种复杂现象的相互比较，可供分析研究之用。

（2）费甚少时间可得明确的概念。

（3）对于专门知识不足的人，亦可得到了解。

（4）表示事务间的关系时，图表较文章可以使阅者印入脑海。

（5）利用于演讲、宣传或广告时，予阅者深刻印象。

（6）有时可用插补法求近似值。

2.图表必备条件：

（1）能把握全体——应一看即能完全了解全体的状况。

（2）简单明了——绘制力求简单明了。

（3）迅速了解——不必任何言辞说明，阅读者一看即能判断出来。

（4）正确的判断——不论刻度标法、线的大小或实虚、点的大小，都应讲求，并使其能正确判断。

（5）浮现对策——最高明的图表是能从图上看出解决问题的对策。

图表之种类

依使用目的分：

1.解析用图表—将过去的数据或现状，作为图表加以解析，从中发现问题点来加以改善。

适于工厂作业分析或研究之用。

如推移图、柏拉图、管制图…

2.管理用图表：

（1）特性要因图—了解品质特性及其所波及之影响。

（2）查检表—知道不良发生的部位。

（3）制程能力图—知道分布中心的倾向及瑕疵程度。

（4）管制图—了解工程的安定状态。

（5）雷达图—了解多项目其前后之变化状况。

几种常用图表介绍

›1.棒形图

›2.扇形图

›3.折线图

›4.带状图

›5.进度图

›6.流程图

›7.Z形图

›8.雷达图

›9.箭头图

›10.点图、体积图、面积图

特性要因图

想获得好的结果，就必须充分的把握何种原因会有好的影响，何种原因会有坏的影响，然后加以管理改善。

何谓特性要因图：

对于结果（特性）与原因（要因）间或所期望之效果（特性）与对策间的关系，以箭头连结，详细分析原因或对策的一种图形称为特性要因图。

特性要因图为日本品管权威学者石川馨博士于1952年所发明，故又称“石川图”。

又因其形状似鱼骨，故亦称鱼骨图。

用在阐明原因与结果的关系，亦称因果图。

特性要因图的画法

步骤1：

决定问题（或品质）的特性。

步骤2：

准备适当的纸张、划制特性要因图的骨架，将特性写在右端，自左划上一条较粗的干线（称母线），就是代表制程，并在干线的右端划一指向右方的箭头。

步骤3：

把原因分类成几个大类，每大类划于中骨上，且以圈起来。

步骤4：

探讨大原因的原因，再细分为中、小原因，将其记入小骨及枝骨上（称孩枝、曾孙枝）。

步骤5：

决定影响问题点原因的顺序。

绘图应注意事项

1.集合全员的知识与经验。

2.应用脑力激盈术，全员发言。

3.把要因层别。

4.把重点放在解决问题上，依5W1H的方法逐项列出。

5.应按特性别绘制多张的特性要因图。

6.原因解析愈细愈好。

绘图应注意事项

7.确认原因的重要程度，应考虑其可行性、价值，并经讨论表决后决定。

8.应将圈出的重要原因整理出来，重新制作另一个特性要因图。

9.记入必要的事项于图旁。

10.品质特性的决定以现场第一线所发生的问题来考虑。

11.管理者避免指示。

12.经过三阶段的酝酿。

特性要因图种类：

1、追求对策型（鱼骨图反转）

追求问题点应如何防止、目标之效果应如何达成等的对策，而以特性要因图表示期望效果（特性）与对策间的关系。

特性要因图种类：

2、追求原因型

在于追求不良的所在，并进而寻找其影响的原因，以特性要因图表示结果（特性）与原因间的关系。

5M法

✍1、作业者（Man）

✍2、机具、设备（Machine）

✍3、原材料（Material）

✍4、方法（Method）

✍5、量规、仪器（Measurement）

5W1H

✍1、What（什么）

✍2、Where（何处）

✍3、When（何时）

✍4、Who（谁）

✍5、Why（为何）

✍6、How（如何）

查检表（Checksheet）

就是一种为了便于收集数据，使用简单记号填记并予统计数据，作进一步分析或作为核对、检查之用而设计的一种表格或图表。

为了便于收集数据，而设计的一种表格或图表。

用很简单的划记、符号、数字记入表格或图表，能一目了然地看出其结果的一种手法、工具。

日常管理改善上，用处大、效率大、效率高、冒险小的工具，是解决问题的先决条件。

分析问题时，能清楚地抓住问题的重心。

查检表的设计要领

1.应能迅速、正确、简易地收集到数据。

2.记录时要考虑到层别。

3.数据履历要清楚。

4.尽可能地以符号、数字记入，避免使用文字。

5.查检项目不宜太多，以4-6项为原则。

6.最好能一次记录下来后，就能表示出图表状况来。

7.如能使用写实图形，更可一目了然。

8.查检表配合目的，必要时检讨修正。

9.预留空位，以供在实际查检中可再增列事先未考虑到的。

查检表的种类

1、记录用（或改善用）查检表

主要功用在于根据收集之数据以调查“不良项目”、“不良主因”、“工程分布”、“缺点位置”等情形。

2、点检用查检表

主要功用是为要确认作业实施、机械整备的实施情形，或为预防发生不良或事故、确保安全时使用。

查检表的作法：

1、明确目的

2、决定查检项目

3、决定抽检方式

4、决定查检方式

5、设计表格实施查检

记录用（或改善用）查检表：

1、决定所要收集的数据及所希望把握的项目

2、决定所要设计的表格形式

3、决定记录的形式

4、决定收集的方法

5、记入记号并整理成次数分配表

点检用查检表：

1、将须点检的项目逐一的列举出来，并空出查检时要记入记号的空栏。

2、所谓须点检的项目是“非做不可的工作”、“非检查不可的事项”等。

3、点检有顺序要求时需注明编号，依顺序排列。

4、点检表必是确实毫无遗漏。

5、必须点检的项目，尽可能以机械、制程人员等层别之。

查检表之使用：

1.有问题必需迅速地采取措施。

2.问题若未获解决,马上研究采取适当措施。

3.查检表的项目应随着工程的改善而改变内容。

4.查检表应能反应出下一工程或市场的关系。

5.不方便随时填记时，以小东西分别代替。

6.由记号即能判断，并采取行动。

7.收集的数据应能获得层别的情报。

8.进行数据收集时，先准备好查检工具。

9.让收集者了解收集目的及方法。

10.收集的数据非所欲得者，检讨后重新收集之。

11.基准需一致。

12.计算单位应符合实际。

13.考虑样本数。

14.用柏拉图整理。

柏拉图：

1、根据所搜集之数据，按不良原因、不良状况、不良发生位置等不同项目，以寻求占最大比率之原因、状况或位置的一种图形。

2、从柏拉图可看出哪一项目的有问题，其影响程度如何，以判断问题的症结点，并针对问题点采取改善措施，故又称ABC图。

柏拉图的作法

1、决定数据的分类项目

a.结果的分类

b.原因的分类

2、决定收集数据之期间，并按上项分类，在期间内收集数据。

3、按发生次数顺序，将项目及次数记入不良分析表。

4、按分类项目别，统计数据作统计表。

5、于图表用纸记入纵轴及横轴。

6、点上累计不良次数（或累计不良率）及累计影响度，并以折线连结则得柏拉图。

7、记入数据收集的期间，记录者、绘图者及总检查数、总不良数……等于图之空白处。

柏拉图之用途：

1.作为降低不良的依据

2.决定改善的攻击目标

3.确认改善效果（改善前、后之比较）

4.应用于发掘现场的重要问题点

5.用于整理报告或记录

6.可作不同条件的评价

7.确认或调整特性要因图

8.柏拉图分析具有“检定假说”之意义

9.配合特性要因图使用—柏拉图上的项目当作品质特性加以要因分析，可以讨论出改善的方案。

哪些数据可以整理为柏拉图

1.品质方面2.时间方面—效率3.成本方面4.安全方面5.营业方面6.交通方面

7.选择方面8.士气方面9.治安方面10.医学方面

层别法：

为区别各种不同的原因对结果之影响而以各别原因为主体，分别作统计分析的方法，称为层别法。

层别法的功用：

层别就是分层别类，依其共通之特性分为一个层，并使层与层间能有明确的区分。

透过各种分层，依各层收集数据以寻找不良所在或最佳条件，以作为改善品质的有效方法。

层别的对象与项目：

1.时间的层别2.作业员的层别3.机械、设备的层别4.作业条件的层别5.原材料的层别6.测定的层别7.检查的层别8.环境、气候的层别9.地区的层别10.制品的层别11.其他

层别法使用注意事项：

1.数据之履历应详细载明。

2.依各种可能原因加经层别，直到找出真正的原因所在。

3.查检表之设计应针对所怀疑的对象来设计。

4.由层别法所获得的情报应付诸实际的行动。

5.实施层别之前，首先确定层别的目的——解析不良率？

提高作业效率？

…...

散布图：

为研究两个变量间之相关性，而搜集成对二组数据，在方格纸上以点来表示出二个特性值之间相关情形的图形，称为“散布图”。

散布图功用：

1.知道两组数据（或原因与结果）之间是否有关及其相关程度。

2.把材料、机械设备、作业者、作业方法……等可能影响的原因层别，绘制散布图，可检讨何者影响结果。

3.检视是否有离岛情形。

4.抽样检验中，若某品质特性之测试成本高或因难，可采用与

此特性有关系存在的另一个测试成本较低或测试容易之特性，以降低检验成本。

5.管制图中，若同一制品之二特性间有密切关系时，则可舍去其中一个管制图，以降低预防成本。

6.两组数据间若呈直线变化，可依散布图求出直线方程式，以作为订定标准之用。

相对应的两组数据间关系的分类：

1.原因（要因）与结果（特性）之关系

2.结果（特性）与其他结果（特性）之关系。

3.结果（特性）与二个原因（要因）间之关系。

散布图之作法：

步骤1：

收集30组以上的相对数据，整理到数据表上（数据不能太少，否则易生误判）。

NNN

OXYOXYOXY

18104711840522181044

28905612870532285053

38504813830522388054

48404514830452488057

58505415820462584050

68905916820482688054

78705017860552783046

88605118870552886052

98104219830492986050

108205320820443084049

XMAX890YMAX59

MIN810MIN42

步骤2：

找出数据x、y之最大及最小值。

XMAX890YMAX59

MIN810MIN42

步骤3：

画出纵轴与横轴（若是判断要因与结果之关系，则横轴代表要因，纵轴代表结果）；并取x及y之最大值与最小值差为等长度画刻度。

Y

X

步骤4：

将各组对数据在横轴与纵轴之数据交会处点上“.“。

步骤5：

记入必要事项

散布图之判读：

散布图之判读：

1.正相关:

x增大时，y也随之增大，称为正相关。

2.非显著性正相关

x增大时，y也随之增大，但增大的幅度不显著。

此时宜再考虑其他可能影响的

要因。

3.负相关:

x增大时，y反而减少，称为负相关。

4.非显著性负相关

x增大时，y反而减各，但幅度并不显著。

此时宜考虑其他可能影响的要因。

5.无相关

（1）x与y之间看不出有何相关关系。

（2）x增大时，y并不改变。

6.曲线相关

x开始增大时，y也随之增大，但达到某一值后，则当x增大时，y却减小。

1.注意有无异常点

2.是否有层别必要

3.是否为假相关

4.勿依据技术、经验作直觉的判断

5.数据太少，容易发生误判

6.调查有无异常原因

散布图之相关检定：

1.符合检定；

步骤1：

作散布图。

步骤2：

于散布图上——纵划分线，使左右之点数相同

于散布图上——横划分线，使上下之点数相同

步骤3：

付予象限号码，并计算各象限之点数

步骤4：

斜对1,3/2,4象限之点数相加，并求全体之点

步骤5：

查符号检定表并判断。

>n

（2）+n（4）+

>n

（1）+n（3）_

基本统计观念：

统计的概念

①统计就是企图掌握数据的差异性。

②长期观察虽因差异性，但乱中有序，都可观察到差异的规则性。

③统计学上将数据的规则性称为“分配”

④利用这些规则性，足以提供管理者进行工作系统的预测，判断而有效地管理。

分配的种类

①由数据的属性，分配可分

计数值数据的分配……间断分配

计量值数据的分配……连续分配

②实务上常可观察到

计数值数据的分配

超几何分配、二项分配、卡氏分配

计量值数据的分配

常态分配

③这些分配已由学者做出数值表，易于查表而应用

掌握分配的方法

①以直方圆掌握，观察要点

分配型态

中心趋势与变异大小

管理者应将分配与规格比较，可得制程能力分析，而实施管理

②使用数字表示

中心趋势……平均值μ

变异趋势……标准差σ

数字掌握分配的方法

①掌握中心趋势

算术平均数X

中位数X

众数XMode

例1：

数据3440424032

平均数X=（34+40+42+40+32）/5=188/5=37.6

中位数X=40

众数Xmode=40

例2：

数据393440424032

平均数X=（39+34+40+42+40+32）/6

=227/6=37.8

中位数X=（40+39）/2=39.5

众数Xmode=40

②掌握变异趋势

全距

R=最大值-最小值

平方和

SS=∑X2-（∑X）2/n

变异数

V=SS/n

标准差

S=√V

数据3440424032

全距R=42-32=10

平方和12345合计（∑X）2

X344042403218835344

X2115616001764160010247144

SS=∑X2-（∑X）2/n=7144-（35344/5）=75.2

变异数V=SS/n=75.2/5=15.04

标准差S=√V=√15.04=3.88

观察样本推论群体

①统计品质管制的作法是从群体中抽出样本测定，藉统计方法以推测、判断群体之状况而采取行动，这种方法可以经济有效实施品质管制

②从样本推论群体，以便对群体进行预测、判断

推论群体的项目与推论方法

对象推论群推论

体项目方法

中心趋势平均值μμe=x

变异趋势标准差σσe=√ve

=√SS/n-1

推论群体的方法

从群体（制程）取n样本，测其特性值

计算平均值X

标准差SS,Ve,√VeVe称不偏变异数，用来估计群体的标准差

样本平均数的分配是常态分配

从中心值为μ、标准差为σ常态分配的制程中，经多次取样，计算平均值，也呈常态分配

中心值为X标准差为σ

可用于预测及判断

统计学上有关母数与统计量的区别

来源群体样本

数据母数统计量

分配母数分配统计量分配

符号μ、σX、S

推测μe、σe☜

管制图的种类

数据种类使用管制图样本大小

计量值X-Rn≥2

Xn=1

计数值Pn不一定

Pnn一定

U单位大小不一

C单位大小一定

选择合适的管制图种类

直方图：

为要容易看出如长度、重量、时间、硬度等计量值的数据之分配情形，所用来表示的图形。

直方图：

直方图是将所收集的测定值或数据之全距分为几个相等的区间作为横轴，并将各区间内之测定值所出现次数累积而成的面积，用柱子排起来的图形，故我们亦称之为柱状图。

直方图制作：

1.制作次数分配表：

（1）由全体数据中找出最大值与最小值。

（2）求出所有数据中之最大值与最小值（即全距）。

（3）决定组数。

（4）决定组距。

：

（5）决定各组上下组界。

：

（6）计算各组的组中点。

（7）作次数分配表。

2.制作直方图

直方图常见之形态

1.正常型：

说明：

中间高、两边低，有集中趋势。

结论：

左右对称分配（常态分配），显示制程在正常运转下。

2.缺齿型（凹凸不平型）：

说明：

高低不一，有缺齿情形。

不正常的分配，系因测定值或换算方法有偏差，次数分配不妥当所形成。

结论：

检查员对测定值有偏好现象，如对5，10之数字偏好；或是假造数据。

测量仪器不精密或组数的宽度不是倍数时，亦有这种情形。

3.偏态型：

说明：

高处偏向一边,另一边低,拖长尾巴。

可分偏右型、偏左型。

为偏态分配。

偏右型；例如微量成分的含有率等，不能取到某值以下的值时，所出现的形状。

3.偏态型：

偏左型：

例如成分含有高纯度的含有率等，不能取到某值以上的值时，就会出现的形状。

结论：

尾巴拖长时，应检讨是否在技术上能够接受。

工具磨损或松动时，亦有这种情形发生。

4.绝壁型（切边型、断裂型）：

说明：

有一端被切断。

结论：

原因为数据经过全检过，或制程本身有经过全检过，会出现的形状。

若剔除某规格以上时，则切边在靠近右边形成。

5.双峰型（二山型）：

说明：

有两个高峰出现。

结论：

有两种分配相混合，例如两台机台或两种不同原料间有差异时，会出现此种形状，因测定受不同的原因影响，应予层别后再作直方图。

6.离岛型（二山脱难型）：

说明：

在右端或左端形成小岛。

结论：

测定有错误、工程调节错误或使用不同原料所引起。

一定有异常原因存在，只要去除，即可制出合乎规格的制品。

7.高原型：

说明：

形状高原状。

结论：

不同平均值的分配混在一起。

应层别之后再作直方图比较。

直方图之应用

1.测知制程能力，作为制程改善的依据

2.计算产品不良率

3.调查是否混入两个以上不同群体

4.测知有无假数据

5.测知分配型态

6.藉以订定规格界限

7.与规格或标准值比较

8.研判所设计的管制界限可否用于管制制程

9.改善前后之比较

品质管制

始于管制图

终于管制图

管制之原理

品质变异之原因

偶然（机遇）原因

异常（非机遇）原因

1.品质变异之原因

1.1偶然（机遇）原因不可避免的原因，可让它存在，是属于管制状态的变异。

（1）由很多微小的原因引起的，而每一个原因所引起的变动都很微小。

（2）同种原料内的变动、机器的震动所引起的变动、熟手作业员的变动，这些对工厂来说是一种正常的变动，也是无法避免的变动。

（3）在制程管制时，想要将此种变动减少或去除，是非常不经济的。

1.2异常（非机遇）原因可避免的原因，不可让它存在，必需追查原因，采取行动，使制程恢复正常，否则会发生莫大的损失。

异常发生的原因：

不遵守操作标准操作。

虽然照操作标准操作，但因各种标准不完善。

以致无法控制变异原因。

使用不合格的原料或材料。

机械发生故障或磨损。

作业员疲劳或情绪欠佳。

2.管制图与常态分配

在生产过程中，如仅有偶然原因的变动时，任何产品之品质特性均可构成一分配，此等分配有其平均数及标准差，在平均数加减三个标准差范围以外之点极少。

2.管制图与常态分配

因此通常都以平均数加减三个标准差作为管制上限与管制下限，此即萧华特博士所创的3σ法。

管制图是以3个标准差为基础，换言之，只要群体是常态分配，从此群体抽样时，每10000个当中，即有27个会跑出±3σ之外，亦即每1000次中约有3次机会超出±3σ范围，此3次是偶然机会跑出界限的，不予计较。

管制图的种类

1.计量值管制图

所谓计量值管制图系管制图所依据之数据均属于由量具实际量测得。

如长度、重量、成份等特性均为连续性者。

（a）平均值与全距管制图

（X-Rchart）

2。

计数值管制图

所谓计数值管制图系管制图所依据之数据均属于以单位计数者。

如不良数、缺点数等间断数据均属之。

（a）不良率管制图

（Pchart）

管制图之绘制

X-R管制图的作法

1）搜集100个以上数据，依测定时间顺序或群体顺序排列。

2）把2-6个（一般采4-5个）数据分为一组。

3）把数据记入数据表。

4）计算各组平均值X。

5）计算各组的全距R

εX

6）计算总平均X=

组数

εR

7）计算总平均R=

组数

8）计算管制界限。

9）绘管制界限，并将点点入图中。

10）记入数据履历入特殊原因，以备查考、分析、判断。

P管制图的作法

1.收集数据，至少20组以上。

2.计算每组之不良率P

总不良率个数

3.计算平均不良率P=

总检查数

P管制图的作法

4.计算管制界限

中心线CL=P

P（1-P）

上限UCL=P+3

n

P（1-P）

上限UCL=P-3

n

P管制图的作法

5.绘管制界限，并将点贴入图中。

6.记入数据履历及特殊原因，以备查考、分析、判断。

管制图之判识

1.管制状态的判断

（1）管制状态

满足下列条件，即可认为制程是在管制状态。

多数之点子集中在中心线附近。

少数之点子落在管制界限附近。

点之分布呈随机状态，无任何规则可循。

没有点子超出管制界限之外。

（2）非管制状态

点在管制界限的线外（或线上）。