圆教学设计.docx

圆教学设计.docx

《圆教学设计.docx》由会员分享，可在线阅读，更多相关《圆教学设计.docx（19页珍藏版）》请在冰豆网上搜索。

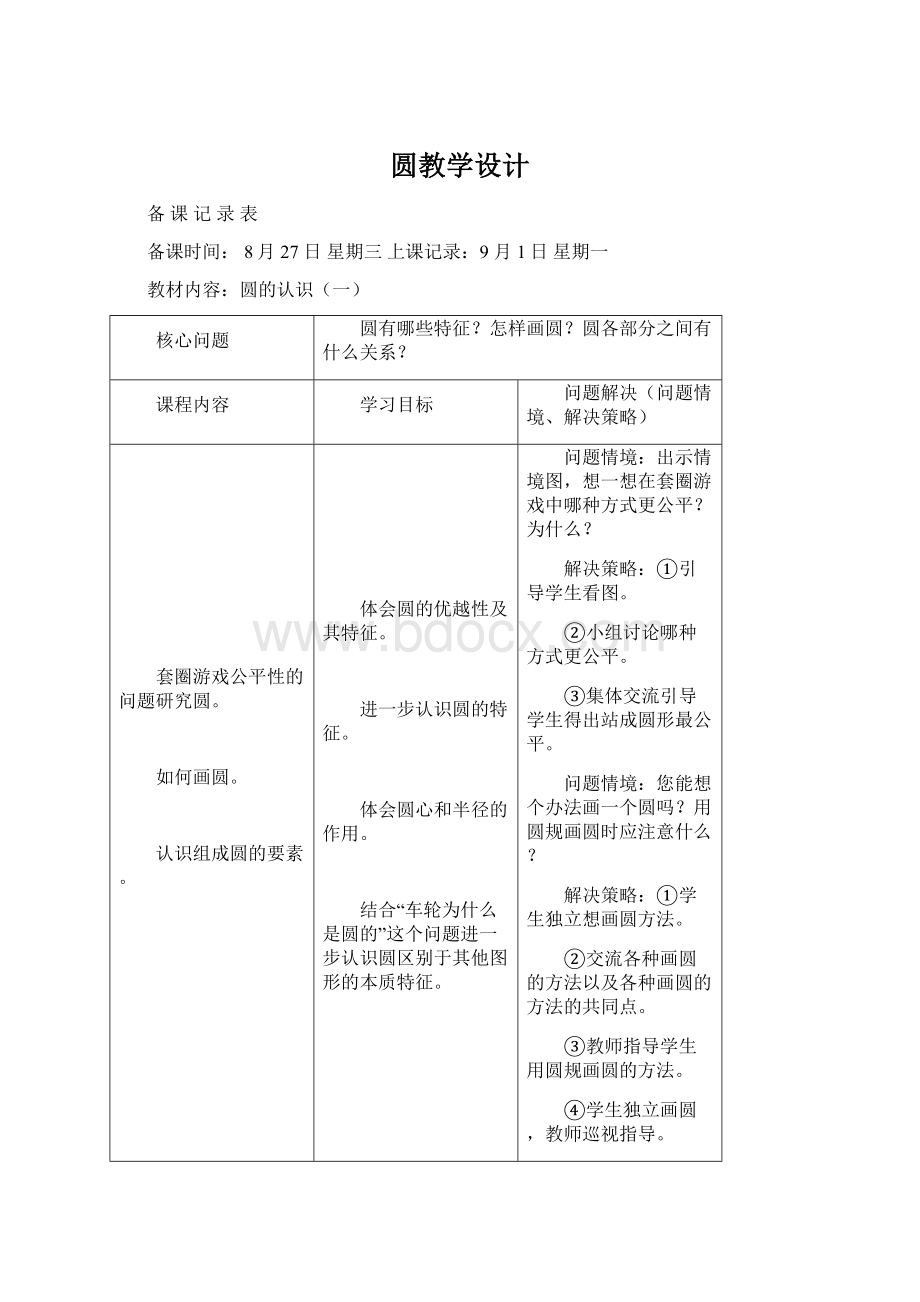
圆教学设计

备课记录表

备课时间：

8月27日星期三上课记录：

9月1日星期一

教材内容：

圆的认识

（一）

核心问题

圆有哪些特征？

怎样画圆？

圆各部分之间有什么关系？

课程内容

学习目标

问题解决（问题情境、解决策略）

套圈游戏公平性的问题研究圆。

如何画圆。

认识组成圆的要素。

体会圆的优越性及其特征。

进一步认识圆的特征。

体会圆心和半径的作用。

结合“车轮为什么是圆的”这个问题进一步认识圆区别于其他图形的本质特征。

问题情境：

出示情境图，想一想在套圈游戏中哪种方式更公平？

为什么？

解决策略：

①引导学生看图。

②小组讨论哪种方式更公平。

③集体交流引导学生得出站成圆形最公平。

问题情境：

您能想个办法画一个圆吗？

用圆规画圆时应注意什么？

解决策略：

①学生独立想画圆方法。

②交流各种画圆的方法以及各种画圆的方法的共同点。

③教师指导学生用圆规画圆的方法。

④学生独立画圆，教师巡视指导。

⑤认识圆的各部分名称。

问题情境：

半径之间、直径之间、半径和直径之间有什么关系？

解决策略：

①学生独立推想

②学生通过画一画、量一量、折一折等方法进行验证。

③集体交流、归纳。

问题情境：

圆的大小和什么有关？

圆的位置与什么有关？

解决策略：

①学生画同心圆，

②学生画几个大小相同的圆。

③观察思考圆的大小与什么有关，圆的位置与什么有关？

④汇报交流。

练习

1.人们在联欢时，会自然围成一个圆形，为什么？

想一想，说一说。

2.画一个半径是1.5厘米的圆，并用字母o,r,d标出它的圆心半径和直径。

3、填表

备课记录表

备课时间：

8月27日星期三上课记录：

9月2日星期二

教材内容：

圆的认识

（一）

核心问题

车轮为什么是圆的

课程内容

学习目标

问题解决（问题情境、解决策略）

圆心到圆上的距离处处相等。

通过“车轮为什么是圆的”这个问题进一步认识圆区别于其他图形的本质特征。

进一步领悟圆的基本特征，灵活运用圆的知识解决实际问题

问题情境：

说一说元有哪些特征？

解决策略：

学生练习说、指名汇报。

问题情境：

车轮为什么是圆的？

解决策略：

①学生小组内用圆、正方形、椭圆代替车轮做实验，组内分工合作。

②用圆形硬纸片做车轮画下圆心运动轨迹。

③用正方形硬纸片做车轮画下圆心运动轨迹。

④用椭圆形硬纸片做车轮画下圆心运动轨迹。

⑤引导学生观察三种车轮中心点的痕迹，思考：

如果把它们分为两类应该怎么分？

根据什么分？

（痕迹是直线还是去曲线）

⑥学生继续讨论圆心的痕迹为什么是直线，以确定圆形车轮到地面的距离就是圆的半径，同一个圆的半径是相等的所以车轮的运动是平稳的。

⑦总结圆和其他图形有什么不同？

练习

1、淘气设计了下面4种自行车的车轮，骑上这样的自行车会怎样？

2、填一填

3、在没有圆规的情况下，你能用哪些方法画圆？

4、您能用圆的知识解释吗？

试着说一说。

①井盖为什么是圆的。

水滴的涟漪为什么是圆的？

备课记录表

备课时间：

8月28日星期四上课记录：

月日星期

教材内容：

圆的认识

（二）

核心问题

圆的对称轴有什么特点？

课程内容

学习目标

问题解决（问题情境、解决策略）

圆的对称性，对称轴特点、对称轴条数。

找圆心

借助折纸活动，探索圆的对称性以及认识圆有无数条对称轴。

不仅找到找出找到一个圆的圆心的方法，认识到两个直径的交点就是圆心。

问题情境：

圆是轴对称图形吗？

有几条对称轴？

解决策略：

①学生回忆轴对称图形的特征。

②学生思考圆是否是轴对称图形，用圆纸片折一折验证。

得出结论。

③学生借助圆纸片思考圆的对称轴有什么特点？

圆的对称轴有多少条？

④同桌交流汇报。

问题情境：

我们学过的图形中哪些是轴对称图形？

有几条对称轴？

解决策略：

①学生独立填写书上表格

②组内交流，互相补充。

③全班汇报。

问题情境：

你有办法找出一个圆的圆心吗？

解决策略：

①学生借助圆形纸片折一折

②交流总结找圆心的方法和理由。

问题情境：

请找出下面各图的对称轴。

解决策略：

①学生独立完成

②展示画出的各图对称轴。

③交流是怎样找到这些图形的对称轴的。

④引导学生思考：

这些图形中都有圆，圆有无数条对称轴，这些组合也有无数条对称轴吗？

练习

1.下面图形是轴对称图形吗？

画出轴对称图形的两条对称轴。

2.小组合作量一量、填一填

3、图中圆的位置发生了什么变化？

备课记录表

备课时间：

8月28日星期四上课记录：

9月4日星期四

教材内容：

欣赏与设计

核心问题

用圆规设计简单图案

课程内容

学习目标

问题解决（问题情境、解决策略）

分析图案形成

模仿图案

设计图案

让学生在欣赏中感受图形世界的美妙。

让学生用圆规画出图案，进一步引导学生分析、了解设计过程。

问题情境：

大屏幕出示，说一说上面这些图案是怎样形成的？

解决策略：

①学生观察思考：

这些图案是有哪些基本图形组成的，怎样组成的？

图案中各图形之间有什么关系？

②学生交流汇报

问题情境：

大屏幕继续出示，看一看，下面的图案是怎样画出来的?

试着画一画。

解决策略：

①学生独立书中呈现的风车画法，自己试着用圆规画，教师巡视指导，交流风车的画法。

②学生观察太极的画法，自己试着用圆规画，教师巡视指导，交流风太极的画法。

问题情境：

你能画出下面的图案吗？

在设计一个有趣的图案与同伴交流。

解决策略：

①学生交流两幅画的画法

②学生自己画草图，在小组内交流自己的设计方案，用圆规设计图案，教师巡视指导。

3展示交流

练习

1.先说一说下面的图案的图案是怎样形成的，再画一画

2.按照下面的方式做一做，注意观察黑点在旋转式的痕迹。

3.用一个圆、三条线段、设计出一个有意义的图形。

4.你能看懂下面两组图的意思吗？

你有什么发现？

备课记录表

备课时间：

9月7日星期日上课记录：

9月9日星期二

教材内容：

圆的周长

核心问题

圆的周长公式是如何推导的？

课程内容

学习目标

问题解决（问题情境、解决策略）

圆周长的含义

测量圆的周长。

探索周长与直径的数量关系。

体会圆周长的意义，同是体现测量曲边图形周长的多样化方法。

学生通过测量和计算，明确圆的周长和直径之间的数量关系，为进一步探索圆的周长计算公式打下基础。

问题情境：

呈现两辆车的图片，思考两辆车的车轮哥滚动一周，谁滚得远？

圆的周长和什么有关？

解决策略：

学生思考理解车轮滚动一周的长度实际上就是车轮的周长，大论滚动一周比小轮滚动一周远，说明圆的周长可能与半径或者直径有关。

问题情境：

如何测量圆的周长？

用圆纸片试一试？

解决策略：

①用圆片代替车轮小组合作共同想办法测量它的周长。

②汇报测量的方法已经测量结果。

③比较结果，大圆的周长亚要大一些。

问题情境：

圆的周长和什么有关？

解决策略：

学生猜测，教师引导学生根据正方形的周长是边长的4倍，类比猜想圆的周长和直径之间也有一定的倍数关系。

问题情境：

找3个大小不同的原片，分别测量出周长和直径，说一说，填一填。

解决策略：

①小组合作通过滚动法和绕线法得出圆的周长。

②测量出圆的直径。

③利用得到的数据计算周长和直径的商，填入表格。

④学生观察表格说说自己的发现。

⑤教师介绍圆周率的相关知识。

练习画一个直径是10厘米的圆

（1）想一想怎样得到它的周长

（2）把圆剪下来，量一量。

（3）多量几次，算出测量结果的平均数。

备课记录表

备课时间：

9月7日星期日上课记录：

9月10日星期三

教材内容：

圆的周长

核心问题

圆的周长公式是如何推导的？

课程内容

学习目标

问题解决（问题情境、解决策略）

圆的周长公式。

运用圆的周长公式进行计算解决实际问题。

在探索周长和直径的关系的基础上，得到圆的周长的计算公式。

通过用用公式解决问题进一步理解圆周长的含义，体会如何形成解题的思路。

问题情境：

你能根据周长和直径的关系，写出圆的周长和直径的计算方法吗？

解决策略：

①根据先前所学的圆的周长和直径的倍数关系，写出圆的周长的计算公式。

②追问：

已知什么条件可以计算圆的周长？

如果知道半径能不能求出圆的周长？

③根据半径与直径的关系，写出根据半径球员的面积的计算公式。

问题情境：

自行车的直径是70厘米，滚动一圈有多远？

解决策略：

①估计滚动一圈会有多远。

②运用公式计算。

③教师补充情境：

儿童滑板车车轮半径是4厘米，滚动一周有多远？

④用公式计算，计较两个车轮的周长，印证车轮越大，运动一周就越远。

问题情境：

你能计算下面图形面积吗？

指出图形边界说一说怎样求出这个图形的周长。

教师利用课件演示理解。

明确周长的一半如何计算。

学生独立计算，全班汇报交流。

教师提问：

大圆周长的一半和小圆的周长有什么关系？

为何说呢么？

引导学生发现图形的周长等于大院的周长。

练习：

书11页

备课记录表

备课时间：

9月7日星期日上课记录：

9月11日星期四

教材内容：

圆周率的历史

核心问题

圆周率的历史

课程内容

学习目标

问题解决（问题情境、解决策略）

阅读资料

培养学生的阅读能力，交流收获，一道学生主动阅读。

通过交流来挖掘圆周率蕴含的教育价值，感受数学的魅力。

问题情境：

与同学交流阅读后的感受，你又知道了那些关于圆周率的知识？

解决策略：

①给学生提供独立的阅读时间，然后交流自己的感受，谈一谈自己大的收获或者交流阅读中有困难、难以理解的地方。

②一到学生在阅读中思考，学会分析问题，提出问题。

问题情境：

收集其他有关圆周率的历史资料，在班上进行展示。

解决策略：

①鼓励学生课前收集有关人类研究圆以及圆周率的资料。

②阅读教科书提供的史料后，交流各自收集的自己资料。

问题情境：

你能根据资料整理一个圆周率的时间表吗？

1学生独立整理

2小组交流，互相补充。

3全班交流展示。

备课记录表

备课时间：

9月7日星期日上课记录：

9月15日星期一

教材内容：

圆的面积

（一）

核心问题

平行四边形和原来的圆有什么关系？

课程内容

学习目标

问题解决（问题情境、解决策略）

复习面积的意义和用方格纸度量面积的方法。

如何把圆转化为学过的图形？

推到圆的面积公式

通过复习进一步了解用方格纸度量面积的方法。

了解“以直代曲”的数学方法。

通过将圆转化为近似的平行四边形推导出圆的面积公式。

问题情境：

如何得到一个圆的面积？

解决策略：

①回顾如何得到一个平行四边形的面积的方法，激活已有数学活动经验。

②小组交流方法

③全班交流总结（数方格，转化成长方形）

④结合教科书记忆学生自己交流得到的方法，思考哪些方法可以算出圆的面积？

不能算出圆的面积的方法中哪种方法更接近圆的面积？

问题情境：

能否将圆转化成以前学过的图形呢？

解决策略：

①学生先将圆8等分，拼一拼，拼成近似的长方形。

②再将圆16等分，拼一拼，看一看，比一比，让学生了解：

“以直代曲”才转化为平行四边形。

问题情境：

看一看，想一想，圆等分的份数越多，拼出的图形越接近于什么形？

解决策略：

①思考怎样使拼成的图形接近于学过的图形

②教师利用课件展示，让学生直观感受平均分的份数越多，欲望无限接近平行四边形。

问题情境：

拼成的平行四边形与原来的圆之间有什么关系？

1名学“联系”指什么

2思考平行四边形的底和高分别与圆有什么联系。

3根据平行四边形的面积公式推导出圆的面积公式。

练习：

书15页

备课记录表

备课时间：

9月7日星期日上课记录：

9月16日星期二

教材内容：

圆的面积

（二）

核心问题

如何运用圆的面积公式求圆的面积？

课程内容

学习目标

问题解决（问题情境、解决策略）

应用圆的面积公式解决实际问题。

已知圆的周长，求圆的面积的实际问题。

要让学生精力解决实际问题的过程。

把实际问题转化为数学问题。

从未知想须知，从已知想可知，大同一直和位置的常用思维模式。

问题情境：

喷水半径是3米喷水头转动一周，能浇灌多大面积的农田？

1学生思考喷水头的浇灌面积其实就是什么？

明确喷水头浇灌的面积就是求半径为3米的圆的面积。

2学生独立应用圆的面积公式解决问题。

3交流方法。

教师追问：

面积公式中r的平方表示什么意思？

问题情境：

凉的圆形羊圈的周长是12.56米，这个羊圈的面积是多少平方米？

解决策略：

教师提问：

学生独立思考，独立解决问题。

②交流方法。

教师追问：

要求圆的面积必须知道什么？

学生思考回答。

如何求出圆的半径？

4师生共同总结。

已知圆的周长求圆面积的方法。

问题情境：

下面是一个有意思的推导圆面积的方法，读一读，填一填。

解决策略：

①学生独立阅读、填空。

②交流总结。

说说三角形与原来的圆有什么联系？

教师追问：

这种推导圆面积的方法关键是什么？

（形状变了，但是大小没变）

练习：

1、一个圆形茶杯垫的半径是4厘米，这个茶杯垫的面积是多少？

2、一个圆形蓄水池的周长是31.4米，它的占地面积是多少平方米？

备课记录表

备课时间：

9月7日星期日上课记录：

9月17日星期三

教材内容：

练习一

核心问题

圆的周长及圆的面积怎样计算

课程内容

学习目标

问题解决（问题情境、解决策略）

范例精讲

针对圆的面积和周长做练习

检测

通过复习回顾上节课所学知识

熟练运用圆的周长和面积公式解决实际问题。

对本节课所学知识进行检测。

了解学生掌握情况

1、说一说,圆的周长怎样计算？

字母公式？

圆的面积面积怎样计算？

字母公式？

2.大屏幕出示例题

①一个圆形花坛，直径是4米，周长是多少米？

②一个圆形花坛，直径是4米，面积是多少平方米？

3、①学生独立思考计算②汇报③小组交流两道题的区别

4、通过刚才的两道题说一说求圆的周长必须知道什么，要求圆的面积必须知道什么？

1.半径是5厘米的半圆的周长是多少？

2.一根绳子长282.6米，绕柱子20圈，求柱子横截面的面积。

3.钟表的分针长5厘米，从2时到3时，

（1）分针的尖端走了多少厘米？

（2）分针扫过的面积是多少平方厘米？

4.王大爷想用31.4米的铁丝在自家的后院围一个菜园，要使面积尽量的大，该围什么图形呢?

面积是多少?

（1）一个圆形茶几的半径是3分米，它的面积是多少平方分米？

（2）一个圆的直径是4米，面积是多少？

（3）一个圆的周长是12.56厘米，求它的面积是多少？

备课记录表

备课时间：

9月7日星期日上课记录：

9月18日星期四

教材内容：

练习一

核心问题

圆的周长及圆的面积怎样计算

课程内容

学习目标

问题解决（问题情境、解决策略）

范例精讲

针对圆的面积和周长做练习

检测

通过复习回顾上节课所学知识

熟练运用圆的周长和面积公式解决实际问题。

对本节课所学知识进行检测。

了解学生掌握情况

1、说一说,圆的周长怎样计算？

字母公式？

圆的面积面积怎样计算？

字母公式？

2.大屏幕出示例题

半径r

直径d

周长c

面积s

2cm

10dm

18.84cm

3、①小组合作计算②汇报交流

4、说一说求圆的周长必须知道什么，要求圆的面积必须知道什么？

一、填空

1.把一个圆平均分成若干等分，然后拼在一起，可以拼成一个近似（）。

长方形的宽是圆的（）,长是圆的（）,求圆面积用公式表示（）。

2.圆规的两脚之间长度是3厘米，画出的圆周长是（）厘米，面积是（）平方厘米。

3.一个圆周长是12.56厘米，它的直径是（）厘米，半径是（）厘米。

二、解决问题

1.一只小羊栓在木桩上，绳子长6米，小羊能吃到草的面积有多大？

2.长12.56米的绳子，正好绕树干10圈。

树干横截面的直径大约是多少？

2.某钟表的分针长10厘米。

（1）从1时到2时，分针尖端走过多少厘米？

（2）从1时到2时，分针扫过的面积是多少平方厘米？