二阶低通有源滤波.docx

二阶低通有源滤波.docx

《二阶低通有源滤波.docx》由会员分享，可在线阅读，更多相关《二阶低通有源滤波.docx（11页珍藏版）》请在冰豆网上搜索。

二阶低通有源滤波

二阶低通有源滤波

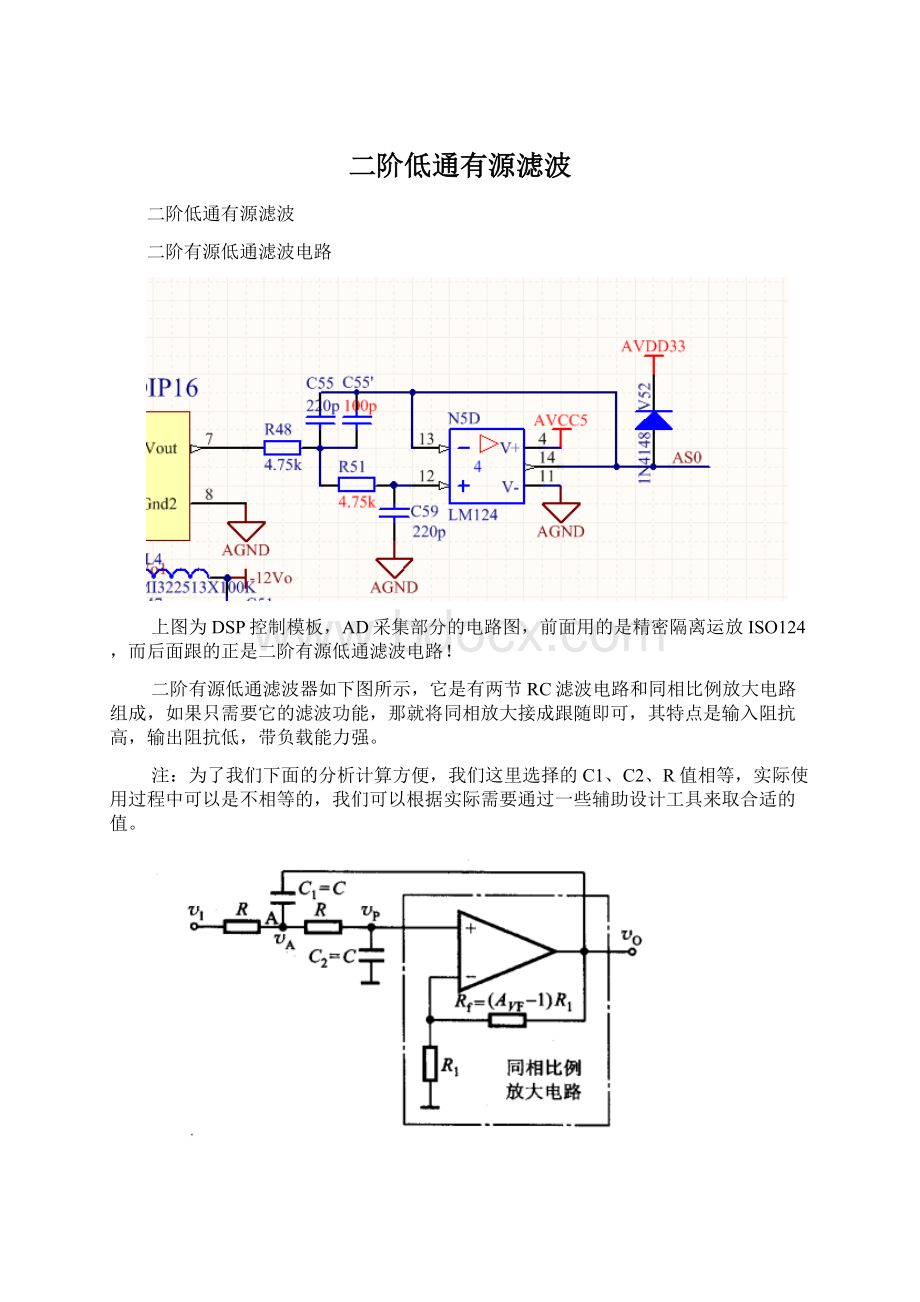
二阶有源低通滤波电路

上图为DSP控制模板，AD采集部分的电路图，前面用的是精密隔离运放ISO124，而后面跟的正是二阶有源低通滤波电路！

二阶有源低通滤波器如下图所示，它是有两节RC滤波电路和同相比例放大电路组成，如果只需要它的滤波功能，那就将同相放大接成跟随即可，其特点是输入阻抗高，输出阻抗低，带负载能力强。

注：

为了我们下面的分析计算方便，我们这里选择的C1、C2、R值相等，实际使用过程中可以是不相等的，我们可以根据实际需要通过一些辅助设计工具来取合适的值。

根据“虚短”和“虚短”，同相比例放大电路的电压增益

。

以上都是摘自模电书本上的解释，这里不免要联想到上面使用的伯德图，还有就是那个为什么Ao>3时就会自激振荡呢？

先来看一看是不是如这个所说的，使用Multisim对其进行仿真，仿真电路如下：

此处可以修改R3、R4的值来调节同相放大电路的增益

当R3、R4都取1k时，输入以1kHz的正弦波信号，此为蓝色为channelA为输出，channelB为输入，可以看出波形还是正常放大

还是保持R3、R4值不变，将输入信号变为50kHz,明显输出减小，说明滤波效果明显，频率高的被衰减了。

当我们取值R3、R4分别为1K、2K时，即Ao=Avf=3时，这是一种临界状态，在仿真图上可以看出输出波形开始出现振荡。

当取值为1K、3K时，即Ao=Avf=4时，此时的输出已经振荡的非常厉害，这也正符合上面讲到的放大电路增益相一致。

这里不免让我们想到了自动控制原理，学完这些课程之后，你会发现其实之中都有联系，只是当时上课的顺序的问题，造成理解不深刻，而且不能站在一定的高度上从全局看问题

在自控的“线性系统的时域分析法“中，实就涉及到了二阶系统的时域分析：

对比上面二阶有源低通滤的传递函数是不是惊人的相似，

令传递函数的分母为0，则得到了二阶系统的特征方程：

他的两个根（闭环极点）为：

单位阶跃响应：

ζ<0,负阻尼，不稳定，发散正弦振荡或单调发散

ζ=0，无阻尼，等幅振荡

0<ζ<1,欠阻尼，，衰减振荡

ζ=1,临界阻尼，非周期的趋于稳态输出

1<ζ,过阻尼，非周期的趋于稳态输出，但响应速度比临界阻尼缓慢

可以看出只要闭环极点在s品面虚轴左半边的都是稳定的，在右半边的则会不稳定，在虚轴上的会出现等幅振荡的情况。

这和根轨迹里面讲闭环极点和稳定性的关系时也可以联系到一起。

自动控制原理“线性系统稳定性分析”指出：

线性系统稳定的充分必要条件是：

闭环系统特征方程的所有根均具有负实部；或者说，闭环传递函数的极点均位于s左半平面。

我们可以使用matlab来对上述进行验证：

如图使用simulink画出传递函数module,注意此处传递函数写的就是闭环的传递函数，如果要画出标准形式，则传递函数的形式为

，

当ζ<0，即分母多项式中s的系数为负值时（-1）：

由图可以看出是不稳定的。

当ζ=0，等幅振荡

当0<ζ<1;即系数小于2时，取值为1，有超调

当ζ=1;即系数等于2时

当ζ>1;即系数大于2时，取值为4，可以看出无振荡，且响应要比临界阻尼快速。