2018高考逆袭系列之导数压轴题的解题技巧.pptx

2018高考逆袭系列之导数压轴题的解题技巧.pptx

《2018高考逆袭系列之导数压轴题的解题技巧.pptx》由会员分享，可在线阅读，更多相关《2018高考逆袭系列之导数压轴题的解题技巧.pptx（51页珍藏版）》请在冰豆网上搜索。

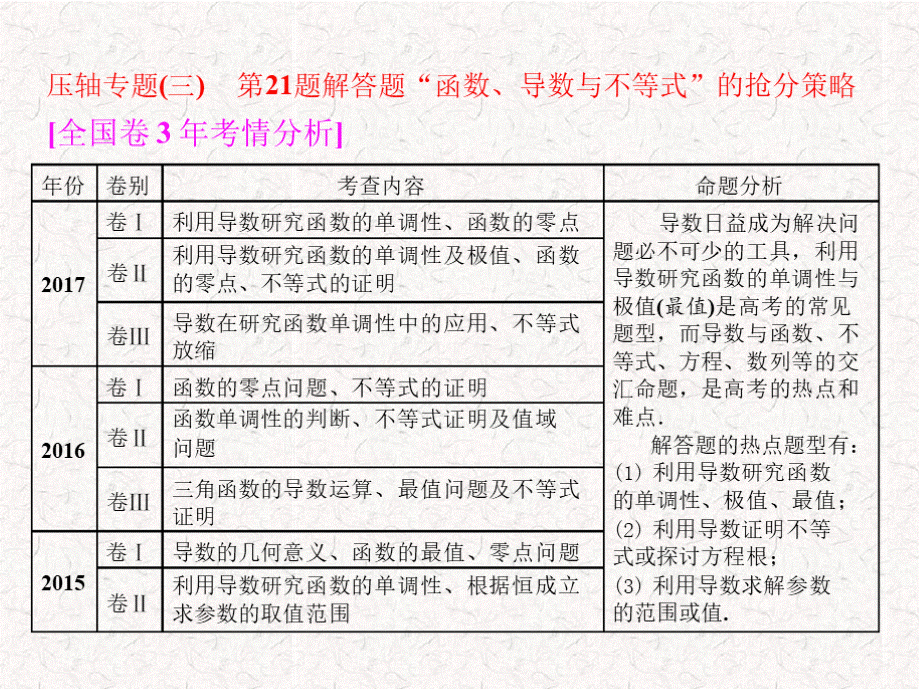
,压轴专题（三）第21题解答题“函数、导数与不等式”的抢分策略,全国卷3年考情分析,2017,命题分析导数日益成为解决问题必不可少的工具，利用导数研究函数的单调性与极值（最值）是高考的常见题型，而导数与函数、不等式、方程、数列等的交汇命题，是高考的热点和难点解答题的热点题型有：

利用导数研究函数的单调性、极值、最值；利用导数证明不等式或探讨方程根；利用导数求解参数的范围或值.,卷,卷,2016,卷,卷,2015,卷,年份卷别考查内容卷利用导数研究函数的单调性、函数的零点利用导数研究函数的单调性及极值、函数的零点、不等式的证明导数在研究函数单调性中的应用、不等式放缩卷函数的零点问题、不等式的证明函数单调性的判断、不等式证明及值域问题三角函数的导数运算、最值问题及不等式证明卷导数的几何意义、函数的最值、零点问题利用导数研究函数的单调性、根据恒成立求参数的取值范围,常考题点逐一突破,利用分类讨论思想探究函数性质x2典例（2017张掖诊断）设函数f（x）2alnx.当a1时，求曲线yf（x）在点（1，f

（1）处的切线方程；求函数f（x）的单调区间和极值x2解

（1）当a1时，f（x）2lnx，,1,则f（x）xx，所以,1,f

（1）0，又f

（1）2，,所以曲线yf（x）在点（1，f

（1）,1,处的切线方程为y2.,x2

（2）由f（x）2alnx，,a,得f（x）xx,x2a,x,（x0）,当a0时，f（x）0，函数f（x）在（0，）上单调递增，函数既无极大值，也无极小值；当a0时，由f（x）0，得xa或xa（舍去）于是，当x变化时，f（x）与f（x）的变化情况如下表：

（,xf（x）,（0，a）,a，）,f（x）,a0a1lna2,所以函数f（x）的单调递减区间是（0，a），单调递增区间是（a，）,函数f（x）在xa处取得极小值f（a）,a1lna,2,，无极大值,综上可知，当a0时，函数f（x）的单调递增区间为（0，），函数f（x）既无极大值也无极小值；当a0时，函数f（x）的单调递减区间是（0，a），单调递增区间a1lna,2,为（a，），函数f（x）有极小值，无极大值,定义域求导数零点列表回答遇见参数要讨论哪一步遇见就在哪一步展开讨论2解答这类题的难点何时讨论参数？

由于题目条件的不同，有的在求零点时讨论，有的在列表时讨论；如何讨论参数？

需要根据题目的条件确定，有时还需参考自变量的取值范围，讨论的关键是做到不重不漏,题后悟通1解答这类题的模板,3aR）若函数f（x）在R上为增函数，求a的取值范围；若函数f（x）在R上不单调时，记f（x）在1,1上的最大值、最小值分别为M（a），m（a），求M（a）m（a）,针对训练,1,3x3xa，xa，,解：

由已知得，f（x）13x3xa，xa，,令,1,3,32,g（x）xxa，则g（x）x10，,所以g（x）在a，）上为增函数令h（x）1xa，则h（x）x1.3x32令h（x）0，得x1，所以h（x）在（，1）和（1，）上是增函数，在（1,1）上为减函数,因为f（x）在R上是增函数，所以h（x）在（，a）上为增函数，所以a1.故a的取值范围为（，1因为函数f（x）在R上不单调，所以a1.当1a1时，f（x）在（，1）上是增函数，在（1，a）上是减函数，在a，）上是增函数，a3所以m（a）3，,24,33,M（a）maxh

（1），g

（1）maxa，a.,42,1a,1,当3aa3，即3时，,M（a）,4,3a，,M（a）m（a）3,1（a33a4）；,4212当3aa3，即3a1时，M（a）a3，M（a）m（a）1a33a2）3（当a1时，f（x）在1,1上是减函数，,所以m（a）h

（1）,2,a3，,M（a）,h

（1）a,2,3.,4,故M（a）m（a）3.,3,1,1a33a4，1a，3,综上，M（a）m（a）3,1a3,13a2，3a1，,4,3，,a1.,利用数形结合思想探究函数的零点,典例,（2017沈阳质检）函数f（x）axxlnx在x1处,取得极值求f（x）的单调区间；若yf（x）m1在定义域内有两个不同的零点，求实数m的取值范围,解

（1）由题意知，f（x）alnx1（x0），f

（1）a10，解得a1，当a1时，f（x）xxlnx，即f（x）lnx，令f（x）0，解得x1；令f（x）0，解得0x1.f（x）在x1处取得极小值，f（x）的单调递增区间为（1，），单调递减区间为（0,1）,

（2）yf（x）m1在（0，）上有两个不同的零点，可转化为f（x）m1在（0，）上有两个不同的根，也可转化为yf（x）与ym1的图象有两个不同的交点，由

（1）知，f（x）在（0,1）上单调递减，在（1，）上单调递增，f（x）minf

（1）1，,由题意得，m11，即m2，当00且x0时，f（x）0；当x时，显然f（x）.,如图，由图象可知，m10，即m1，由可得2m1.故实数m的取值范围为（2，1）,题后悟通,利用导数探究函数零点的一般思路转化为可用导数研究其函数的图象与x轴（或直线yk）在该区间上的交点问题利用导数研究该函数在该区间上的单调性、极值（最值）、端点值等性质，进而画出其图象结合图象求解,针对训练,x,2设函数f（x）lnxm，mR.,

（1）当me（e为自然对数的底数）时，求f（x）的极小值；,

（2）讨论函数g（x）f（x）,x,3零点的个数,e,解：

（1）由题设，当me时，f（x）lnxx，则f（x）,xe,x2，,当x（0，e）时，f（x）0，f（x）在（0，e）上单调递减，当x（e，）时，f（x）0，f（x）在（e，）上单调递增，,e,e当xe时，f（x）取得极小值f（e）lne2，,f（x）的极小值为2.,3xx3,x1mx

（2）由题设g（x）f（x）2（x0），,1,3,3,令g（x）0，得mxx（x0）,设,1,3,3,（x）xx（x0），,则（x）x21（x1）（x1）当x（0,1）时，（x）0，（x）在（0,1）上单调递增；当x（1，）时，（x）0，（x）在（1，）上单调递减x1是（x）的唯一极值点，且是极大值点，因此x1也是（x）的最大值点，,（x）的最大值为

（1）2.又（0）0，3结合y（x）的图象（如图），可知，,2,当m3时，函数g（x）无零点；,2,当m3时，函数g（x）有且只有一个零点；,2当0m3时，函数g（x）有两个零点；当m0时，函数g（x）有且只有一个零点,2,综上所述，当m3时，函数g（x）无零点；,2,当m3或m0时，函数g（x）有且只有一个零点；,2,当0m3时，函数g（x）有两个零点.,利用函数思想证明不等式,1x,典例（2017兰州诊断）已知函数f（x）axlnx在（1，,）上是增函数，且a0.

（1）求a的取值范围；,

（2）若b0，试证明,1ab,b,aba,b.,解

（1）f（x）1,1ax1,ax2xax2,，,因为在（1，）上f（x）0，且a0，,1,所以ax10，即xa，,1,所以a,1，即a1.,故a的取值范围为1，）,

（2）证明：

因为b0，a1，所以,ab,b,1，,1x,又f（x）axlnx在（1，）上是增函数，,所以f,abb,f

（1），即,1,ab,b,a,b,abln,ab,b,1,0，化简得,ab,ab,b,，,ln,aba,ab,bb,aaa,b等价于lnbln1bb0，,令g（x）ln（1x）x（x（0，），,则g（x）,1,1x1x,x10，,所以函数g（x）在（0，）上为减函数，,aaa,所以gbln1bbln,ab,b,a,bg（0）0，即ln,b,aba,b.,综上，,1,ab,b,aba,b，得证,题后悟通1利用导数证明不等式的基本步骤作差或变形构造新的函数h（x）利用导数研究h（x）的单调性及最值根据单调性及最值，得到所证不等式,2构造辅助函数的四种方法移项法：

证明不等式f（x）g（x）（f（x）0（f（x）g（x）0），进而构造辅助函数h（x）f（x）g（x）构造“形似”函数：

对原不等式同解变形，如移项、通分、取对数；把不等式转化为左右两边是相同结构的式子的结构，根据“相同结构”构造辅助函数主元法：

对于（或可化为）f（x1，x2）A的不等式，可选x1（或x2）为主元，构造函数f（x，x2）（或f（x1，x）放缩法：

若所构造函数最值不易求解，可将所证明不等式进行放缩，再重新构造函数,题后悟通,针对训练,3（2018届高三西安八校联考）已知函数f（x）exmx3，g（x）ln（x1）2.

（1）若曲线yf（x）在点（0，f（0）处的切线斜率为1，求实数m的值；

（2）当m1时，证明：

f（x）g（x）x3.解：

（1）因为f（x）exmx3，所以f（x）exm3x2.因为曲线yf（x）在点（0，f（0）处的切线斜率为1，所以f（0）em1，解得m0.,

（2）证明：

因为f（x）exmx3，g（x）ln（x1）2，所以f（x）g（x）x3等价于exmln（x1）20.当m1时，exmln（x1）2ex1ln（x1）2.要证exmln（x1）20，只需证明ex1ln（x1）20，,设h（x）ex1ln（x1）2，则h（x）ex1,1,x1,.,设p（x）ex1,1,x1,（x1），,则p（x）ex1,1x1,20.,所以函数p（x）h（x）ex1,1,x1,在（1，）上单调递增,因为h,1,2,1e220，h（0）e10，,所以函数h（x）ex1,1,x1,0,在（1，）上有唯一零点x，,1,且x02，0.,因为h（x0）0，所以e,0,x1,1,x01,，,即ln（x01）（x01）,当x（1，x0）时，h（x）0；当x（x0，）时，h（x）0，,所以当xx0时，h（x）取得最小值h（x0）,0,x,1,0,所以h（x）h（x0）eln（x1）2,1,x01,0,（x1）,20.综上可知，当m1时，f（x）g（x）x3.,利用转化与化归思想求解恒成立问题,典例（2018届高三皖南八校联考）已知函数f（x）lnx.求函数g（x）f（x1）x的最大值；若对任意x0，不等式f（x）axx21恒成立，求实数a的取值范围,解

（1）f（x）lnx，g（x）f（x1）xln（x1）x（x1），,g（x）,1,x1x1,x1.,当x（1,0）时，g（x）0，g（x）在（1,0）上单调递增；当x（0，）时，g（x）0，g（x）在（0，）上单调递减g（x）在x0处取得最大值g（0）0.,

（2）对任意x0，不等式f（x）axx21恒成立，,a,lnx,x，,1,axx,在x0上恒成立，,lnx进一步转化为,x,max,ax,1,xmin,，,lnx1lnx设h（x）x，则h（x）x2，当x（1，e）时，h（x）0；当x（e，）时，h（x）0，,h（x）在xe处取得极大值也是最大值,max,h（x）,1,e,.,要使f（x）ax恒成立，必须a,1,e.,另一方面，当x0时，x12，当且仅当x1时等号成,x立，要使axx21恒成立，必须a2，,满足条件的a的取值范围是12.e，,题后悟通,利用转化与化归思想解决不等式恒成立问题的“两种”常用方法

（1）分离参数法：

（2）函数思想法：

针对训练,a,4（2017陕西质检）已知函数f（x）lnx2x2（a1）x.,

（1）若曲线yf（x）在x1处的切线方程为y2，求f（x）的单调区间；,

（2）若x0,2,fxfx时，x恒成立，求实数a的取值范围,x,1解：

（1）由已知得f（x）ax（a1），则f

（1）0.,而f

（1）ln1,aa,22,（a1）1，,a,2,曲线yf（x）在x1处的切线方程为y,1.,2,a，解得,12a2.,f（x）lnxx23x（x0），f（x）,1,x,2x3.,1,由