 工程力学答案.docx
工程力学答案.docx
- 文档编号:7110553
- 上传时间:2023-01-18
- 格式:DOCX
- 页数:30
- 大小:311.72KB
工程力学答案.docx
《工程力学答案.docx》由会员分享,可在线阅读,更多相关《工程力学答案.docx(30页珍藏版)》请在冰豆网上搜索。
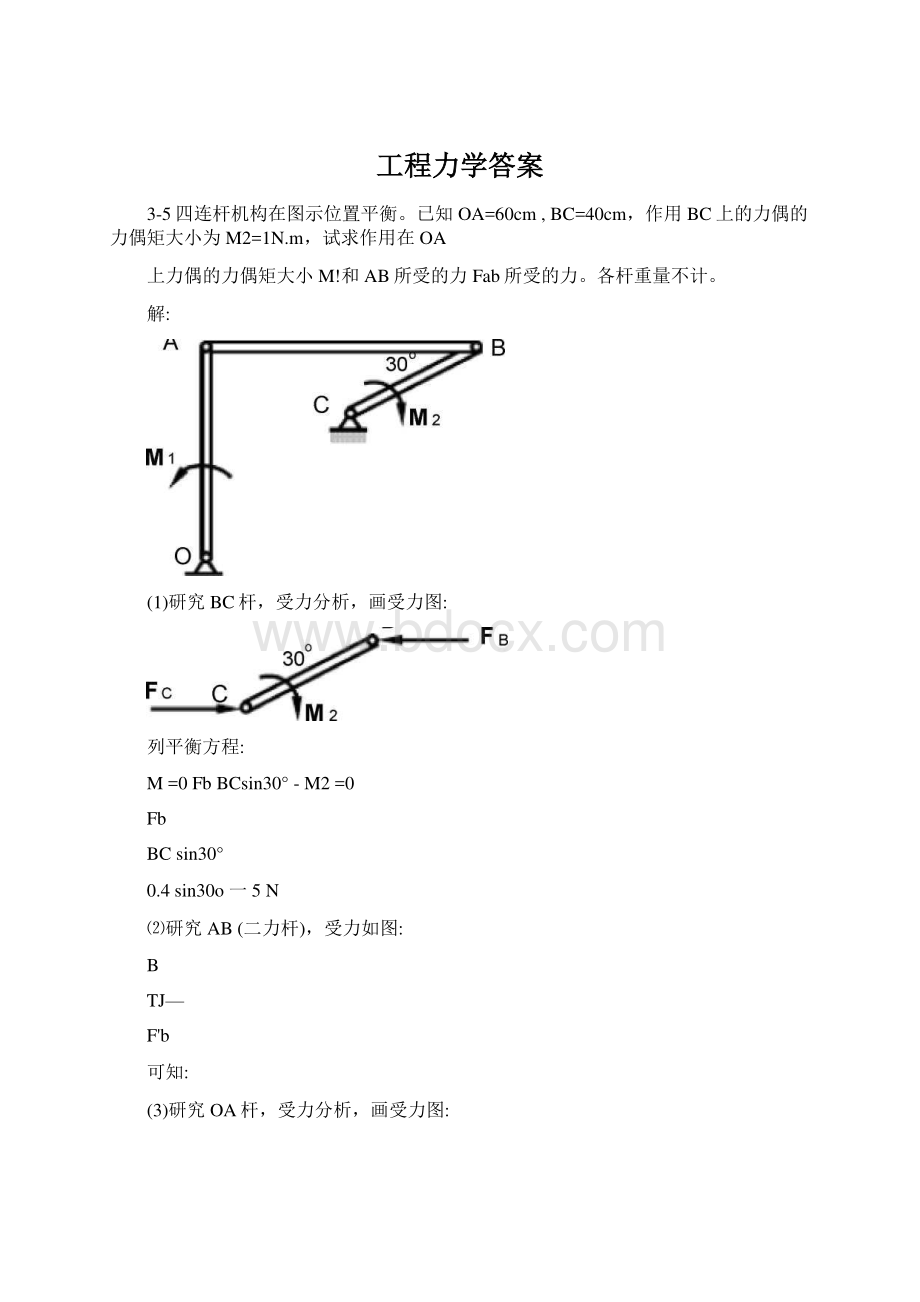
工程力学答案工程力学答案3-5四连杆机构在图示位置平衡。
已知OA=60cm,BC=40cm,作用BC上的力偶的力偶矩大小为M2=1N.m,试求作用在OA上力偶的力偶矩大小M!
和AB所受的力Fab所受的力。
各杆重量不计。
解:
(1)研究BC杆,受力分析,画受力图:
列平衡方程:
M=0FbBCsin30-M2=0FbBCsin300.4sin30o一5N研究AB(二力杆),受力如图:
BTJFb可知:
(3)研究OA杆,受力分析,画受力图:
列平衡方程:
M=0FaOAM0MlFaOA=50.6=3Nm3-8在图示结构中,各构件的自重都不计,在构件BC上作用一力偶矩为M的力偶,各尺寸如图。
求支座A的约束力。
l解:
(1)取BC为研究对象,受力分析,画受力图;FcMb(平面任意力系);M=0-FCIM=0FC斗
(2)取DAC为研究对象,受力分析,画受力图;DoFDSAD-FCXA画封闭的力三角形;FD11兰解得FFFC2MFcos45。
=4-5AB梁一端砌在墙内,在自由端装有滑轮用以匀速吊起重物D,设重物的重量为G,又AB长为b,斜绳与铅垂线成:
角,求固定端的约束力。
ybMaBAaGFayFAx解:
(1)研究AB杆(带滑轮),受力分析,画出受力图选坐标系Bxy,列出平衡方程;Fx二0:
-FAxGsin:
-0Fax=Gsin:
Fy=0:
FAy-G-Gcos:
=0FAy二二G(1cos:
):
)MB(F)=0:
MA-FAybGR-GR=0MA二G(1cos:
)b4-16由AC和CD构成的复合梁通过铰链C连接,它的支承和受力如题4-16图所示。
已知均布载荷集度q=10kN/m,力偶M=40kNm,a=2m,不计梁重,试求支座A、B、D的约束力和铰链C所受的力。
解:
(1)研究CD杆,La-a*a.一.a.,画出受力图(平面平行力系);吗aa*x
(2)选坐标系Cxy,列出平衡方程;aMe(F)=0:
-pqdxxM-Fd2a=0FD=5kNa乞Fy=0:
FcJ0q沢dx-F=0Fe二25kN(3)研究ABC杆,受力分析,画出受力图(平面平行力系);7qdxa,一ax选坐标系Bxy,列出平衡方程;axMB(F)=0:
FAa-qdxx-FCa=0J0Fa=35kNa为为Fy=0:
-Fa-Joqx:
dx+Fb-Fc=0Fb二80kN4-18由杆AB、BC和CE组成的支架和滑轮E支持着物体。
物体重12kN。
D处亦为铰链连接,尺寸如题4-18图所示。
试求固定铰链支座A和滚动铰链支座B的约束力以及杆BC所受的力。
解:
xFx=0:
FaxW=0Fax=12kN、Ma(F)=0:
FB4-W1.5-rW2r=0FB二10.5kNF厂0:
FaFb-W=0Fa1.5kN(3)研究CE杆(带滑轮),受力分析,画出受力图(平面任意力系);FDyCB选D点为矩心,列出平衡方程;Md(F)=0:
Fcbsin:
1.5-W1.5-rWr=0Fcb二15kN约束力的方向如图所示。
4-19起重构架如题4-19图所示,尺寸单位为mm。
滑轮直径d=200mm,钢丝绳的倾斜部分平行于杆BE。
吊起的载荷W=10kN,其它重量不计,求固定铰链支座A、B的约束力。
选坐标系Bxy,列出平衡方程;Mb(F)=0:
FAx600-W1200=0Fax=20kN、Fx二0:
-FaxFbx二0Fbx二20kNF厂0:
-FAyFmyW二0(3)研究ACD杆,受力分析,画出受力图(平面任意力系);FAxCFdJdFcFDxFay(4)选D点为矩心,列出平衡方程;、MD(F)=0:
FAy800-Fc100=0Fa1.25kN(5)将FAy代入到前面的平衡方程;FbFAyW=11.25kN约束力的方向如图所示。
4-20AB、AC、DE三杆连接如题4-20图所示。
DE杆上有一插销F套在AC杆的导槽内。
求在水平杆DE的E端有一铅垂力F作用时,AB杆上所受的力。
设AD=DB,DF=FE,BC=DE,所有杆重均不计。
研究DFE杆,解:
(1)整体受力分析,根据三力平衡汇交定理,可知B点的约束力一定沿着BC方向;受力分析,画出受力图(平面任意力系分别选F点和研究ADB杆,FdTFfFZ/45OB点为矩心,列出平衡方程;受力分析,画出受力图Mf(F)=0:
Mb(F)=0:
(平面任意力系xFDyFDxEFFDyDE=0EDFDxDB二0=2F选坐标系Axy,列出平衡方程;MA(F)=0:
FDxAD-FbAB=0Fb二F一Fx-0:
-Fax-FbFdx二0Fax二F1Fy-0:
_FAyFDyFaF-06-9已知物体重W=100N,斜面倾角为30(题6-9图a,tan30=0.577),物块与斜面间摩擦因数为解:
(1)确定摩擦角,并和主动力合力作用线与接触面法向夹角相比较;WFrtgf=fs=0.38Vtg=tg30=0.577f=20.8V:
判断物体的状态,求摩擦力:
物体下滑,物体与斜面的动滑动摩擦力为F=fs*Wcosa=32N物体有向上滑动趋势,且静滑动摩擦力达到最大时,全约束力与接触面法向夹角等于摩擦角;画封闭的力三角形,求力F;w_fsin90-:
fsin:
ff=gfsin90-fW=82.9N6-10重500N的物体A置于重400N的物体B上,B又置于水平面C上如题图所示。
已知fAB=0.3,fBc=0.2,今在A上作用一与水平面成30的力F。
问当F力逐渐加大时,是A先动呢?
还是A、B一起滑动?
如果B物体重为200N,情况又如何?
解:
(1)确定A、B和B、:
fi二二arctgfAB=16.7o2二二arctgfBc=11.3当A、B间的静滑动摩擦力达到最大时,画物体A的受力图和封闭力三角形;A上F30FR1FR1Waf11flWasin:
f1F1sin180-f1-90-30sinf1sin60。
一。
一f1W-209N当B、C间的静滑动摩擦力达到最大时,画物体A与B的受力图和封闭力三角形;o比较Fi和F2;F2Wabsin180o-f2-90o-30sinf2Wa厂厂234Nsin60oj:
f2物体A先滑动;(4)如果Wb=200N,则Wa+b=700N,再求F2;sinf2F2f2WAb=183N2sin60-f2FF2物体A和B一起滑动;6-11均质梯长为1,重为P,B端靠在光滑铅直墙上,如图所示,已知梯与地面的静摩擦因数fsA,求平衡时于?
(A点约束力用全约束力表示);解:
(1)研究AB杆,当A点静滑动摩擦力达到最大时,画受力图由三力平衡汇交定理可知,P、Fb、Fr三力汇交在D点;找出乔n和:
f的几何关系;lsin%tanJcos%211tan%2tanf2fsA01丁min=arctanf2fsA(3)得出堀的范围;190_二二-arctan2fsA8-1试求图示各杆的轴力,并指出轴力的最大值。
(b)2叫I.F3kN2kN(d)(c)解:
(a)
(1)用截面法求内力,取1-1、2-2截面;128取1-1截面的左段;1FN1(b)(c)
(1)二Fx-0F-Fn1=0Fn1=F取2-2截面的右段;FN222、Fx二0-FN2=0FN2=0轴力最大值:
Nmax求固定端的约束反力;FrFr二F取1-1截面的左段;FN1=0F-Fn1=0取2-2截面的右段;2-1FFrN2Fx=0_Fn2_Fr=0FN2=_Fr=_F轴力最大值:
ff用截面法求内力,取Nmax13kN22kN33-i-卄3-3截面;1-1、2-2、2kN
(2)取1-1截面的左段;取2-2截面的左段;Fn1二-2kN取3-3截面的右段;FN3轴力最大值:
(d)
(1)用截面法求内力,取取1-1截面的右段;FN1取2-2截面的右段;轴力最大值:
FN2、Fx=02-3Fn2=01-1、2-2截面;Fn2=1kNFn3=3kN2kNFNmax-3kN1kN1kN、Fx=02-1-Fn广0Fn广广1kN2FN22、Fx=0-1-FN2=0Fn2一1kNFNmax-1kN10-2.试建立图示各梁的剪力与弯矩方程,并画剪力与弯矩图。
解:
(C)
(1)求约束反力Cl/2(C)1/2qBCFs2二F(I/2VXiYl)M2二一FIx2(l/2乞xil)X2xiRa二FRc二2F列剪力方程与弯矩方程FS1=-F(0Yx3I/2)M1=-Fx1(0乞xI/2)画剪力图与弯矩图(d)
(1)Fsi-F(+)(-)FxBAU1r11Jf11r1J1xql/4列剪力方程与弯矩方程Fs(0乞xYi)4Mi二Gx_qx24画剪力图与弯矩图6图面上K点处的弯曲正应力。
xFi=2F2=5kN,试计算梁内的最大弯曲正应力,及该应力所在截1m解:
(1)画梁的弯矩图1myz最大弯矩(位于固定端)Mmax二7.5kN最大应力:
计算应力:
MmaxmaxWzMmaxbh2675汉汉1062=176MPa4080K点的应力:
MmaxIzMmaxbh3MPa40803121217610U二802310=0.92MPaIx在集度为算梁内的最大弯曲正应力,已知钢的弹性模量11-8图示简支梁,No28工字钢制成,q的均布载荷作用下,测得横截面C底边的纵向正应变E=200Gpa,a=1m。
-48=3.0M0,试计*cRapHTRb解:
(1)求支反力Ra二二3qaRb1=4qa
(2)画内力图fs:
pa/4(+)(-)qa/4xx(3)由胡克定律求得截面C下边缘点的拉应力为:
-Cmax=;E=3.010*2001060MPa也可以表达为:
2qa+CmaxWzWz(4)梁内的最大弯曲正应力:
匚maxmaxWz小29qa32Wz9匚匚Cmax=67.5MPa811-15图示矩形截面钢梁,承受集中载荷F与集度为q的均布载荷作用,试确定截面尺寸bo已知载荷F=10kN,q=5N/mm,许用应力c=160Mpao解:
(1)求约束力:
Ra二3.75kNmRB=11.25kNm
(2)画出弯矩图:
x(3)依据强度条件确定截面尺寸max3.75106Wzbh26Mmax3.75106,!
3160MPa4b6-解得:
11-17图示外伸梁,承受载荷b丄丄32.7mm已知载荷F=20KN,许用应力(j=160Mpa,试选择工字钢型号。
F作用。
F解:
(1)求约束力:
(2)画弯矩图:
x20kNmRB=25kNm(3)依据强度条件选择工字钢型号max62010W.1-160MPa解得:
W-125cm3查表,选取No16工字钢梁内最大弯曲正应力超过许用应力30%。
为了消除此种过载,配置一11-20当载荷F直接作用在简支梁AB的跨度中点时,辅助梁CD,试求辅助梁的最小长度l3mr亠3mJrRBRaC.“D14XB解:
(1)当F力直接作用在梁上时,弯矩图为:
解得:
二二30%k-.1
(2)配置辅助梁后,弯矩图为:
x依据弯曲正应力强度条件:
Cmax,2Mmax,2W3FFa将式代入上式,解得:
a=1.385m15-3图示两端球形铰支细长压杆,弹性模量E=200Gpa,试用欧拉公式计算其临界载荷。
(1)圆形截面,d=25mm,1=1.0m;
(2)矩形截面,h=2b=40mm,1=1.0m;(3)No16工字钢,I=2.0m。
lz解:
(1)圆形截面杆:
两端球铰:
尸1,二d48I1.91064n2EIPcr12(田)二二200101.910=37.8kN矩形截面杆矩形截面杆:
两端球铰:
尸1,Iy|z.I厂曲厂曲=2.610-8m12JEIyPcr22(h)298二二200102610=52.6kNNO16工字钢杆工字钢杆:
两端球铰:
尸1,Iy108m4江2EIyPcr3*229二二2001093.110_8=459kN15-8图示桁架,由两根弯曲刚度EI荷F的极限值。
相同的等截面细长压杆组成。
设载荷F与杆AB的轴线的夹角为匕且0虫二/2,试求载解:
(1)分析铰B的受力,画受力图和封闭的力三角形:
两杆的临界压力:
012二11tg60E1二E2AB和BC皆为细长压杆,则有:
Pcr12-EI112Pcr2122(3)两杆同时达到临界压力值,F为最大值;Pcr2=PcrltgVPcr2Pcr1tg=
(1)2二二ctg2600由铰B的平衡得:
1-arctg-FCOST-巳r1El.104而:
2Elcost33a215-12解:
yh/b的最佳值。
当压杆在x之平面内失稳时,可取“=Aiy0.7l在X-平面内弯曲时的柔度;zAlzh.12iz考虑两个平面内弯曲的等稳定性;b、,、,120.7.121b
- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 工程力学 答案
 冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。


 对中国城市家庭的教育投资行为的理论和实证研究.docx
对中国城市家庭的教育投资行为的理论和实证研究.docx
