 高三高考数学国步分项分类题及析答案九.docx
高三高考数学国步分项分类题及析答案九.docx
- 文档编号:7047126
- 上传时间:2023-01-16
- 格式:DOCX
- 页数:11
- 大小:95.88KB
高三高考数学国步分项分类题及析答案九.docx
《高三高考数学国步分项分类题及析答案九.docx》由会员分享,可在线阅读,更多相关《高三高考数学国步分项分类题及析答案九.docx(11页珍藏版)》请在冰豆网上搜索。
高三高考数学国步分项分类题及析答案九
高三高考数学国步分项分类题及析答案九
2-7 一次函数、二次函数及复合函数
基础巩固强化
1.若方程x2-2mx+4=0的两根满足一根大于2,一根小于2,则m的取值范围是( )
A.(-∞,-) B.(,+∞)
C.(-∞,-2)∪(2,+∞)D.(2,+∞)
[答案] D
[解析] 设f(x)=x2-2mx+4,则题设条件等价于f
(2)<0,即4-4m+4<0⇒m>2,故选D.
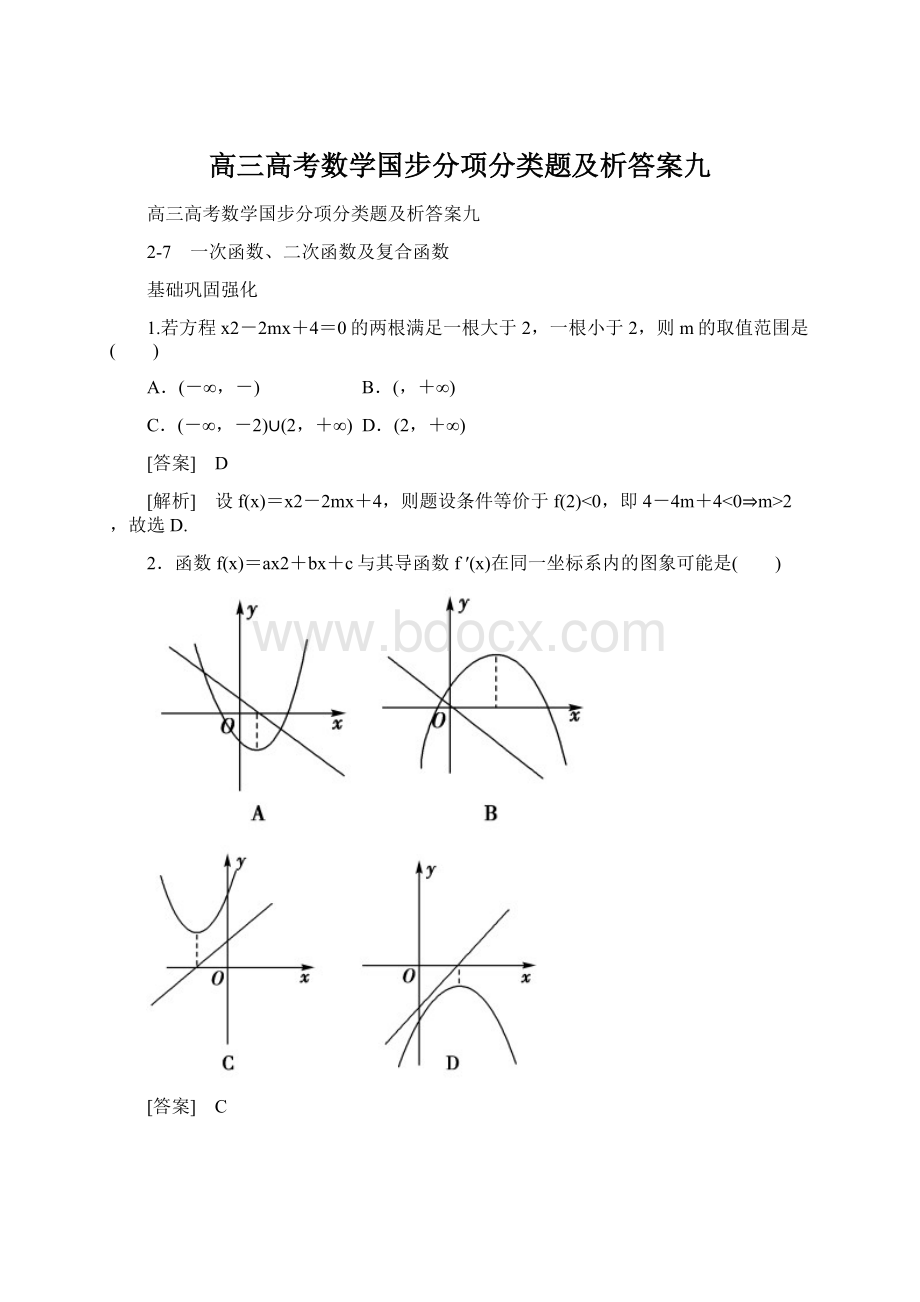
2.函数f(x)=ax2+bx+c与其导函数f′(x)在同一坐标系内的图象可能是( )
[答案] C
[解析] 若二次函数f(x)的图象开口向上,则导函数f′(x)为增函数,排除A;同理由f(x)图象开口向下,导函数f′(x)为减函数,排除D;又f(x)单调增时,f′(x)在相应区间内恒有f′(x)≥0,排除B,故选C.
3.(文)(2011·济南模拟)已知二次函数f(x)图象的对称轴是x=x0,它在区间[a,b]上的值域为[f(b),f(a)],则( )
A.x0≥bB.x0≤a
C.x0∈(a,b)D.x0∉(a,b)
[答案] D
[解析] ∵f(x)在区间[a,b]上的值域为[f(b),f(a)],且f(x)为二次函数,
∴f(x)在[a,b]上单调递减,
又f(x)对称轴为x=x0,开口方向未知,
∴x0≤a或x0≥b,即x0∉(a,b).
(理)若方程2ax2-x-1=0在(0,1)内恰有一解,则a的取值范围为( )
A.a<-1B.a>1
C.-1 [答案] B [解析] 令f(x)=2ax2-x-1,当a=0时,显然不合题意. ∵f(0)=-1<0,f (1)=2a-2, ∴由f (1)>0得a>1,又当f (1)=0,即a=1时,2x2-x-1=0两根x1=1,x2=-不合题意,故选B. 4.函数f(x)对任意x∈R,满足f(x)=f(2-x).如果方程f(x)=0恰有2013个实根,则所有这些实根之和为( ) A.0B.2013 C.4026D.8052 [答案] B [解析] ∵x∈R时,f(x)=f(2-x),∴f(x)的图象关于直线x=1对称,实根之和为1×2013=2013. 5.已知方程|x|-ax-1=0仅有一个负根,则a的取值范围是( ) A.a<1B.a≤1 C.a>1D.a≥1 [答案] D [解析] 数形结合判断. 6.(2011·广东肇庆二模)已知函数f(x)=则不等式f(x)≥x2的解集是( ) A.[-1,1]B.[-2,2] C.[-2,1]D.[-1,2] [答案] A [解析] 依题意得 或⇒-1≤x≤0或0 ⇒-1≤x≤1,故选A. [点评] 可取特值检验,如x=-2,2可排除B、C、D. 7.(2012·上海)已知y=f(x)是奇函数.若g(x)=f(x)+2且g (1)=1,则g(-1)=________. [答案] 3 [解析] 本题考查了奇函数的定义及函数值的求法. ∵f(x)为奇函数,∴f(-1)=-f (1), ∵g (1)=f (1)+2 ①,g(-1)=f(-1)+2 ②, ∴①+②得g (1)+g(-1)=4, ∴g(-1)=4-g (1)=3. [点评] 抓住已知条件f(x)的奇函数是解决本题的关键. 8.(2011·佛山二检)若函数f(x)=ax+b(a≠0)的一个零点是1,则函数g(x)=bx2-ax的零点是________. [答案] 0或-1 [解析] 由题意知ax+b=0(a≠0)的解为x=1,∴b=-a,∴g(x)=-ax2-ax=-ax(x+1),令g(x)=0,则x=0或x=-1. 9.函数f(x)=(a+1)x+2a在[-1,1]上的值有正有负,则实数a的取值范围是________. [答案] (-,1) [解析] 由条件知,f(-1)·f (1)<0, ∴(a-1)(3a+1)<0,∴- 10.(文)已知函数f(x)=x2+2x+3在[m,0]上有最大值3,最小值2,则m的取值范围是________. [答案] [-2,-1] [解析] f(x)=x2+2x+3=(x+1)2+2,对称轴x=-1,开口向上,f(-1)=2,∴m≤-1. 又f(0)=f(-2)=3,∴m≥-2,故m∈[-2,-1]. (理)设函数f(x)=x2+(2a-1)x+4,若x1 [答案] (-∞,) [解析] 由题意得>0,得a<. 能力拓展提升 11.已知命题p: 关于x的函数y=x2-3ax+4在[1,+∞)上是增函数,命题q: 函数y=(2a-1)x为减函数,若“p且q”为真命题,则实数a的取值范围是( ) A.(-∞,]B.(0,) C.(,]D.(,1) [答案] C [解析] 命题p等价于≤1,即a≤.命题q: 由函数y=(2a-1)x为减函数得: 0<2a-1<1,即 12.(2012·浙江宁波模拟)函数f(x)的定义域为(-∞,1)∪(1,+∞),且f(x+1)为奇函数,当x>1时,f(x)=2x2-12x+16,则直线y=2与函数f(x)图象的所有交点的横坐标之和是( ) A.1 B.2 C.4 D.5 [答案] D [解析] 该函数图象与直线y=2有三个交点(x1,2),(x2,2),(x3,2),x1=-1,x2+x3=6(其中(x2,2),(x3,2)关于直线x=3对称),则横坐标之和为5. 13.(2011·福建质检)设二次函数f(x)=ax2-2ax+c在区间[0,1]上单调递减,且f(m)≤f(0),则实数m的取值范围是( ) A.(-∞,0]B.[2,+∞) C.(-∞,0]∪[2,+∞)D.[0,2] [答案] D [解析] 二次函数f(x)=ax2-2ax+c在区间[0,1]上单调递减,则a≠0,f′(x)=2a(x-1)<0,x∈[0,1], 所以a>0,即函数的图象开口向上,对称轴是直线x=1. 所以f(0)=f (2),则当f(m)≤f(0)时,有0≤m≤2. 14.(文)已知函数f(x)=x2-2x+2的定义域和值域均为[1,b],则b等于________. [答案] 2 [解析] ∵f(x)=(x-1)2+1,∴f(x)在[1,b]上是增函数,f(x)max=f(b),∴f(b)=b, ∴b2-2b+2=b,∴b2-3b+2=0,∴b=2或1(舍). (理)(2011·江南十校联考)已知函数f(x)的自变量的取值区间为A,若其值域也为A,则称区间A为f(x)的保值区间.函数f(x)=x2的形如[n,+∞)(n∈(0,+∞))的保值区间是________. [答案] [1,+∞) [解析] 因为f(x)=x2在[n,+∞)(n∈(0,+∞))上单调递增,所以f(x)在[n,+∞)上的值域为[f(n),+∞),若[n,+∞)是f(x)的保值区间,则f(n)=n2=n,解得n=1. 15.(文)若函数y=lg(3-4x+x2)的定义域为M.当x∈M时,求f(x)=2x+2-3×4x的最值及相应的x的值. [解析] 要使函数y=lg(3-4x+x2)有意义,应有3-4x+x2>0, 解得x<1或x>3,∴M={x<1或x>3}. f(x)=2x+2-3×4x=4×2x-3×(2x)2, 令2x=t,∵x<1或x>3,∴t>8或0 ∴y=4t-3t2=-3(t-)2+(t>8或0 由二次函数性质可知, 当0 当t>8时,f(x)∈(-∞,-160); 当2x=t=,即x=log2时,y=. 综上可知,当x=log2时,f(x)取到最大值为,无最小值. (理)已知二次函数f(x)=ax2+bx+c(a≠0)且满足f(-1)=0,对任意实数x,恒有f(x)-x≥0,并且当x∈(0,2)时,有f(x)≤2. (1)求f (1)的值; (2)证明a>0,c>0; (3)当x∈[-1,1]时,函数g(x)=f(x)-mx(x∈R)是单调函数,求证: m≤0或m≥1. [解析] (1)对x∈R,f(x)-x≥0恒成立, 当x=1时,f (1)≥1, 又∵1∈(0,2),由已知得f (1)≤2=1, ∴1≤f (1)≤1,∴f (1)=1. (2)证明: ∵f (1)=1,f(-1)=0,∴a+b+c=1, a-b+c=0,∴b=.∴a+c=. ∵f(x)-x≥0对x∈R恒成立, ∴ax2-x+c≥0对x∈R恒成立, ∴∴∴c>0,故a>0,c>0. (3)证明: ∵a+c=,ac≥,由a>0,c>0及a+c≥2,得ac≤,∴ac=,当且仅当a=c=时,取“=”. ∴f(x)=x2+x+. ∴g(x)=f(x)-mx=x2+x+=[x2+(2-4m)x+1]. ∵g(x)在[-1,1]上是单调函数, ∴2m-1≤-1或2m-1≥1,∴m≤0或m≥1. *16.(文)(2011·西安检测)设函数f(x)=x2+|2x-a|(x∈R,a为实数). (1)若f(x)为偶函数,求实数a的值; (2)设a>2,求函数f(x)的最小值. [分析] (1)f(x)为偶函数⇒f(-x)=f(x)⇒a=0. (2)含绝对值的函数的实质是分段函数,可以通过对x取值的分类讨论,去掉绝对值符号,得到分段函数. [解析] (1)由f(x)为偶函数知,f(-x)=f(x), 即|2x-a|=|2x+a|,解得a=0. (2)f(x)= 当x≥a时,f(x)=x2+2x-a=(x+1)2-(a+1), 由a>2,x≥a,得x>1,故f(x)在x≥a时单调递增,f(x)的最小值为f=; 当x 故当1≤x<时,f(x)单调递增,当x<1时,f(x)单调递减, 则f(x)的最小值为f (1)=a-1. 由-(a-1)=>0,知f(x)的最小值为a-1. (理)(2011·山东实验中学三诊)已知函数f(x)=,x∈[1,+∞). (1)当a=时,求函数f(x)的最小值; (2)若对任意x∈[1,+∞),f(x)>0恒成立,试求实数a的取值范围. [解析] (1)当a=时,f(x)=x++2. ∵x≥1时,f′(x)=1->0, ∴f(x)在区间[1,+∞)上为增函数, ∴f(x)在区间[1,+∞)上的最小值为f (1)=. (2)解法1: 在区间[1,+∞)上, f(x)=>0恒成立⇔x2+2x+a>0恒成立⇔a>-x2-2x恒成立⇔a>(-x2-2x)max,x≥1. ∵-x2-2x=-(x+1)2+1, ∴当x=1时,(-x2-2x)max=-3, ∴a>-3. 解法2: 在区间[1,+∞)上,f(x)=>0恒成立⇔x2+2x+a>0恒成立. 设y=x2+2x+a,x∈[1,+∞), ∴y=x2+2x+a=(x+1)2+a-1递增, ∴当x=1时,ymin=3+a, 当且仅当ymin=3+a>0时,函数f(x)>0恒成立, ∴a>-3. 1.(2011·平顶山模拟)已知函数y=x2-2x+3在闭区间[0,m]上有最大值3,最小值2,则m的取值范围是( ) A.[1,+∞)B.[0,2] C.[1,2]D.(-∞,2] [答案] C [解析] 如图所示. ∵f(x)=x2-2x+3=(x-1)2+2, ∵f(0)=3,f (1)=2,且f (2)=3,可知只有当m∈[1,2]时,才能满足题目的要求. 2.设abc>0,二次函数f(x)=ax2+bx+c的图象可能是( ) [答案] D [解析] 若a<0,则只能是A或B选项,A中-<0,∴b<0,从而c>0,与A图不符;B中->0,∴b>0,∴c<0,与B图不符.若a>0,则抛物线开口向上,只能是C或D选项,当b>0时,有c>0与C、D图不符,当b<0时,有c<0,此时->0,f(0)=c<0,故选D. 3.已知f(x)=(x-a)(x-b)-2(a A.α C.a<α [答案] A [解析] 设g(x)=(x-a)(x-b),则f(x)=g(x)-2,分别作出这两个函数的图象,如图所示,可得α 4.(2011·山东淄博一模)若a<0,则下列不等式成立的是( ) A.2a>()a>(0.2)a B.(0.2)a>()a>2a C.()a>(0.2)a>2a D.2a>(0.2)a>()a [答案] B [解析] 若a<0,则幂函数y=xa在(0,+∞)上是减函数, 所以(0.2)a>()a>0.所以(0.2)a>()a>2a. 5.(2012·江苏,5)函数f(x)=的定义域为________. [答案] (0,] [解析] 要使函数有意义,应有被开方数大于或等于零. 由题意知1-2log6x≥0,∴log6x≤, ∴log6x≤log6,∴0 ∴函数的定义域为(0,]. 6.已知关于x的函数f(x)=x2-2x-3,若f(x1)=f(x2)(x1≠x2),则f(x1+x2)等于________. [答案] -3 [解析] ∵二次函数f(x)=x2-2x-3中,a=1,b=-2,c=-3,∴由f(x1)=f(x2)得,=-=1, 所以x1+x2=2,则f(x1+x2)=f (2)=-3. 7.(2011·南京模拟)已知函数f(x)=x2+abx+a+2b(a>0,b>0),若f(0)=4,则f (1)的最大值为________. [答案] 7 [解析] ∵f(0)=4,∴a+2b=4, ∴f (1)=ab+a+2b+1=ab+5, ∵a>0,b>0,∴4=a+2b≥2, ∴ab≤2,等号在a=2b=2,即a=2,b=1时成立. ∴f (1)=ab+5≤7. 8.(2011·福建武夷山模拟)已知函数f(x)=ax2+(b-8)x-a-ab(a≠0),当x∈(-3,2)时,f(x)>0;当x∈(-∞,-3)∪(2,+∞)时,f(x)<0. (1)求f(x)在[0,1]内的值域; (2)c为何值时,不等式ax2+bx+c≤0在[1,4]上恒成立. [解析] (1)由题意得x=-3和x=2是函数f(x)的零点且a≠0,则 解得,∴f(x)=-3x2-3x+18. (1)如图,由图象知,函数f(x)在[0,1]内单调递减, ∴当x=0时,y=18,当x=1时,y=12, ∴f(x)在[0,1]内的值域为[12,18]. (2)解法1: 令g(x)=-3x2+5x+c. ∵g(x)在上单调递减,要使g(x)≤0在[1,4]上恒成立,则需要g(x)max=g (1)≤0, 即-3+5+c≤0,解得c≤-2. ∴当c≤-2时,不等于ax2+bx+c≤0在[1,4]上恒成立. 解法2: 不等式-3x2+5x+c≤0在[1,4]上恒成立, 即c≤3x2-5x,在[1,4]上恒成立. 令g(x)=3x2-5x,∵x∈[1,4], ∴g(x)在[1,4]上单调递增, ∴g(x)min=g (1)=3×12-5×1=-2,∴c≤-2.
- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 三高 数学 国步分项 分类 答案
 冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。


 对中国城市家庭的教育投资行为的理论和实证研究.docx
对中国城市家庭的教育投资行为的理论和实证研究.docx
