材料科学基础复习题答案.docx

材料科学基础复习题答案.docx

《材料科学基础复习题答案.docx》由会员分享，可在线阅读，更多相关《材料科学基础复习题答案.docx（30页珍藏版）》请在冰豆网上搜索。

材料科学基础复习题答案

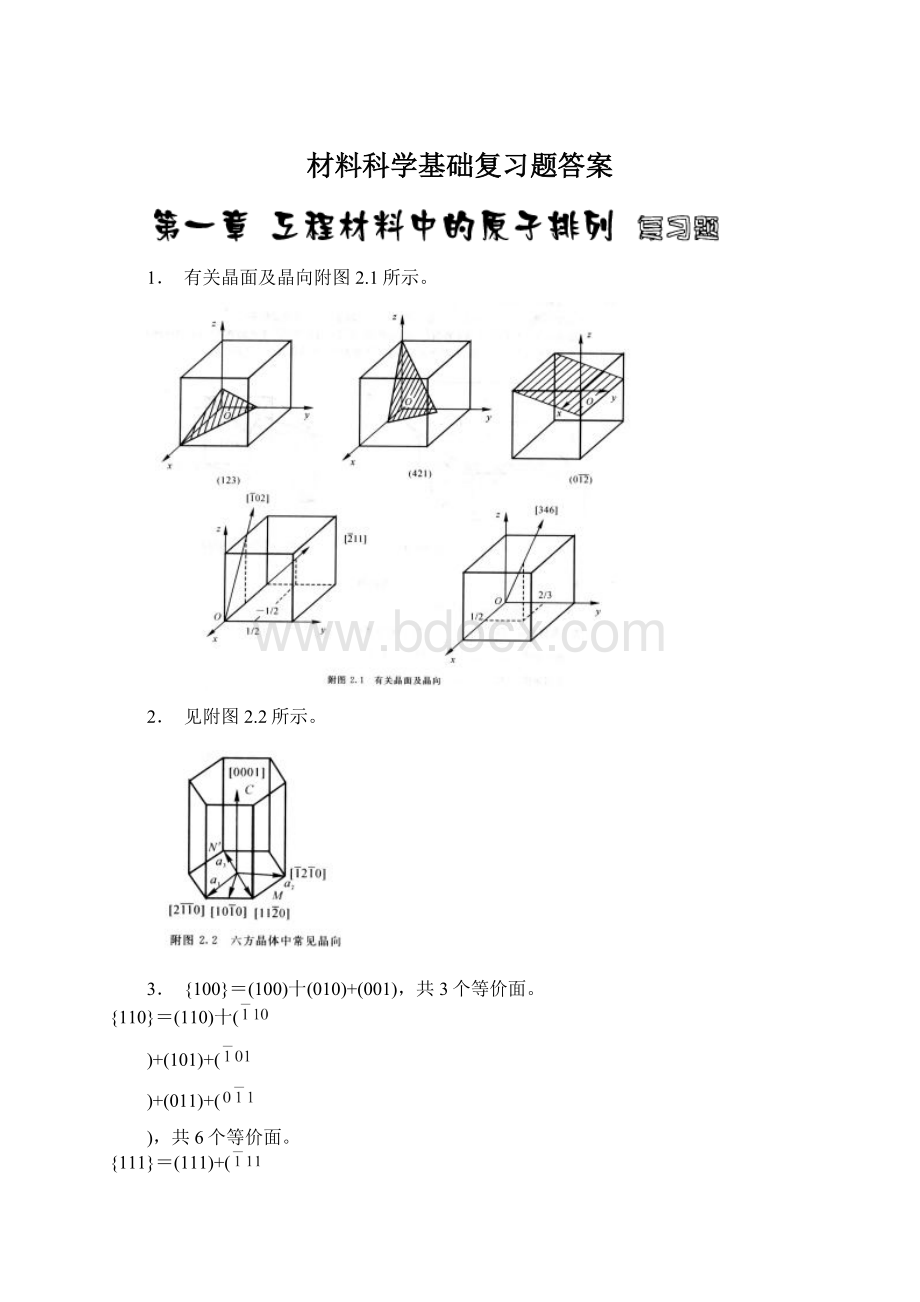
1． 有关晶面及晶向附图2.1所示。

2． 见附图2.2所示。

3． {100}＝（100）十（010）+（001），共3个等价面。

{110}＝（110）十（

）+（101）+（

）+（011）+（

），共6个等价面。

{111}＝（111）+（

）+（

）+（

），共4个等价面。

共12个等价面。

 4． 单位晶胞的体积为VCu＝0.14nm3（或1.4×10-28m3）

 5． 

（1）0.088nm；

（2）0.100nm。

 6． Cu原子的线密度为2.77×106个原子/mm。

Fe原子的线密度为3.50×106个原子/mm。

 7． 1.6l×l013个原子/mm2；1.14X1013个原子/mm2；1.86×1013个原子/mm2。

 8． 

（1）5.29×1028个矽原子/m3；  

（2）0.33。

 9． 9.0.4×10-18/个原子。

 10．             1.06×1014倍。

 11．              

（1）这种看法不正确。

在位错环运动移出晶体后，滑移面上、下两部分晶体相对移动的距离是由其柏氏矢量决定的。

位错环的柏氏矢量为b，故其相对滑移了一个b的距离。

（2）A'B'为右螺型位错，C'D'为左螺型位错；B'C'为正刃型位错，D'A'为负刃型位错。

位错运动移出晶体后滑移方向及滑移量如附图2.3所示。

 12．             

（1）应沿滑移面上、下两部分晶体施加一切应力τ0，的方向应与de位错线平行。

（2）在上述切应力作用下，位错线de将向左（或右）移动，即沿着与位错线de垂直的方向（且在滑移面上）移动。

在位错线沿滑移面旋转360°后，在晶体表面沿柏氏矢量方向产生宽度为一个b的台阶。

13．             

（1）

，其大小为

，其方向见附图2.4所示。

（2）位错线方向及指数如附图2.4所示。

 14．             

（1）能。

几何条件：

∑b前＝∑b后＝

；能量条件：

∑b前2＝

>∑b后2＝

（2）不能。

能量条件：

∑b前2＝∑b后2，两边能量相等。

（3）不能。

几何条件：

∑b前＝a/b[557]，∑b后＝a/b[11¯1]，不能满足。

（4）不能。

能量条件：

∑b前2＝a2 <∑b后2＝

，即反应后能量升高。

 15．             

（1）能够进行。

因为既满足几何条件：

∑b前＝∑b后＝

，又满足能量条件：

∑b前2＝

>∑b后2＝

（2）b合＝

；该位错为弗兰克不全位错。

 16．             

（1）假设晶体中位错线互相缠结、互相钉扎，则可能存在的位错源数目

个／Cm3。

（2）τNi＝1.95×107Pa。

 17．             当θ＝1°，D＝14nm；θ＝10°，D＝1.4nm时，即位错之间仅有5～6个原子间距，此时位错密度太大，说明当θ角较大时，该模型已不适用。

 18．             畸变能是原来的0.75倍（说明形成亚晶界后，位错能量降低）。

19．             设小角度晶界的结构由刃型位错排列而成，位错间距为D。

晶界的能量γ由位错的能量E构成，设l为位错线的长度，由附图2.5可知，

由位错的能量计算可知，

取R＝D（超过D的地方，应力场相互抵消），r0＝b和θ＝b/D代入上式可得：

式中

 20．             

（1）晶体点阵也称晶体结构，是指原子的具体排列；而空间点阵则是忽略了原子的体积，而把它们抽象为纯几何点。

（2）密排六方结构。

（3）原子半径发生收缩。

这是因为原子要尽量保持自己所占的体积不变或少变[原子所占体积VA＝原子的体积（4/3πr3+间隙体积]，当晶体结构的配位数减小时，即发生间隙体积的增加，若要维持上述方程的平衡，则原子半径必然发生收缩。

（4）不能。

因为位错环是通过环内晶体发生滑移、环外晶体不滑移才能形成。

（5）外力在滑移面的滑移方向上的分切应力。

（6）始终是柏氏矢量方向。

（7）位错的交割。

（8）共格界面。

（9）否，扭转晶界就由交叉的同号螺型位错构成。

1． 其比较如附表2.1所示。

附表2.1 间隙固溶体与间隙化合物的比较

类   别

间隙固熔体

间隙化合物

相同点

一般都是由过渡族金属与原子半径较小的C，N，H，O，B等非金属元素所组成

不同点

晶体结构

属于固熔体相，保持熔剂的晶格类型

属于金属化合物相，形成不同于其组元的新点阵

表达式

用α、β、γ等表示

用化学分子式MX，M2X等表示

机械性能

强度、硬度较低，塑性、韧性好

高硬度、高熔点，甥性、韧性差

2． 有序固熔体，其中各组元原子分别占据各自的布拉菲点阵——称为分点阵，整个固熔体就是由各组元的分点阵组成的复杂点阵，也叫超点阵或超结构。

这种排列和原子之间的结合能（键）有关。

结合能愈大，原子愈不容易结合。

如果异类原子间结合能小于同类原子间结合能，即EAB<（EAA十EBB）/2，则熔质原子呈部分有序或完全有序排列。

有序化的推动力是混合能参量（εm＝εAB－1/2（EAA+EBB））εm<0，而有序化的阻力则是组态熵；升温使后者对于自由能的贡献（-TS）增加，达到某个临界温度以后，则紊乱无序的固熔体更为稳定，有序固熔体消失，而变成无序固熔体。

3． 在原子尺寸因素相近的情况下，上述元素在Ag中的固熔度（摩尔分数）受原子价因素的影响，即价电子浓度e/a是决定固熔度（摩尔分数）的一个重要因素。

它们的原子价分别为2，3，4，5价，Ag为1价，相应的极限固熔度时的电子浓度可用公式c＝ZA（1一xB）＋ZBxB

计算。

式中，ZA，ZB分别为A，B组元的价电子数；xB为B组元的摩尔分数。

上述元素在固溶度（摩尔分数）极限时的电子浓度分别为1.43，1.42，1.39，1.31。

4． Α-Fe为体心立方点阵，致密度虽然较小，但是它的间隙数目多且分散，因而间隙半径很小：

r四=0.291，R＝0.0361nm；r八＝0.154，R＝0.0191nm。

H，N，C，B等元素熔人。

α-Fe中形成间隙固熔体，由于尺寸因素相差很大，所以固熔度（摩尔分数）都很小。

例如N在α-Fe中的固熔度（摩尔分数）在590℃时达到最大值，约为WN＝0.1/l0-2，在室温时降至WN＝0.001/l0-2；C在α-Fe中的固溶度（摩尔分数）在727℃时达最大值，仅为WC＝0.02l8/10-2，在室温时降至WC＝0.006/10-2。

所以，可以认为碳原子在室温几乎不熔于α-Fe中，微量碳原子仅偏聚在位错等晶体缺陷附近。

假若碳原子熔入。

α-Fe中时，它的位置多在α-Fe的八面体间隙中心，因为。

α-Fe中的八面体间隙是不对称的，形为扁八面体，[100]方向上间隙半径r＝0.154R，而在[110]方向上，r＝0.633R，当碳原子熔入时只引起一个方向上的点阵畸变。

硼原子较大，熔人间隙更为困难，有时部分硼原子以置换方式熔人。

氢在α-Fe中的固熔度（摩尔分数）也很小，且随温度下降时迅速降低。

以上元素在γ-Fe。

中的固熔度（摩尔分数）较大一些。

这是因为γ-Fe具有面心立方点阵，原子堆积致密，间隙数目少，故间隙半径较大：

rA＝0.414，R＝0.0522nm；r四＝0.225，R＝0.0284nm。

故上述原子熔入时均处在八面体间隙的中心。

如碳在γ-Fe中最大固熔度（质量分数）为WC＝2.1l/10-2；氮在γ-Fe中的最大固熔度（质量分数）约为WN＝2.8/10-2。

5． 密度ρ＝5.97g／cm3。

6． 两离子的中心距离为0.234nm。

7． 碳原子占据10.2％的八面体间隙位置；氮原子占据12.5％的八面体间隙位置。

8． 这是因为形成固熔体时，熔质原子的熔入会使熔剂结构产生点阵畸变，从而使体系能量升高。

熔质与熔剂原子尺寸相差越大，点阵畸变的程度也越大，则畸变能越高，结构的稳定性越低，熔解度越小。

一般来说，间隙固熔体中熔质原子引起的点阵畸变较大，故不能无限互溶，只能有限熔解。

9． 9 

（1）0.278nm；

（2）0.393nm（3）0.482nm；（4）0.622nm；（5）0.393nm。

10．             

（1）WLi+＝16/10-2，WMg2+＝24/1020，WF-＝44/10-2，WO2—＝16/10-2

（2）该固熔体的密度ρ＝2.9g／cm3。

11．             故理论强度介于

之间，即4900～7000MPa

12．             模子的尺寸l＝15.0mm。

13．             

故可能是丙酮。

14．             画出丁醇（C4H9OH）的4种可能的异构体如下：

15．             

（1）单体质量为12X2+1X2+35.5X2＝97g／mol；

（2）聚合度为 n＝60000/97＝620。

16．             

（1）均方根据长度4.65nm；

（2）分子质量m＝7125g。

17．             理论上的最大应变为3380％。

18．             单体的摩尔分数为:

X苯烯＝20/10-2，X丁二烯＝40/10-2，X丙烯晴＝40/10-2

19．             

（1）和

（2）如下：

（3）每摩尔的水（0.6X1024）形成时，需要消去0.6X1024的C—O及N—H键，同时形成0．6X1024的C—N及H—O键。

净能量变化为-15kJ／mol。

20．             硅酸盐结构的基本特点：

（1）硅酸盐的基本结构单元是[Si04]四面体，硅原子位于氧原子四面体的间隙中。

硅—氧之间的结合键不仅是纯离子键，还有相当的共价键成分。

（2）每一个氧最多只能被两个[Si04]四面体所共有。

（3）[Si04]四面体可以是互相孤立地在结构中存在，也可以通过共顶点互相连接。

（4）Si—O--Si的结合键形成一折线。

硅酸盐分成下列几类：

（1）含有有限硅氧团的硅酸盐；

（2）链状硅酸盐；

（3）层状硅酸盐；

（4）骨架状硅酸盐。

21．             因为大多数陶瓷主要由晶相和玻璃相组成，这两种相的热膨胀系数相差较大，由高温很快冷却时，每种相的收缩不同，所造成的内应力足以使陶瓷器件开裂或破碎。

22．             陶瓷材料中主要的结合键是离子键及共价键。

由于离子键及共价键很强，故陶瓷的抗压强度很高，硬度极高。

因为原子以离子键和共价键结合时，外层电子处于稳定的结构状态，不能自由运动，故陶瓷材料的熔点很高，抗氧化性好，耐高温，化学稳定性高。

1． 分析结晶相变时系统自由能的变化可知，结晶的热力学条件为∆G<0；由单位体积自由能的变化

可知，只有∆T>0，才有∆GB<0。

即只有过冷，才能使∆G<0。

动力学条件为液—固界面前沿液体的温度T

由临界晶核形成功A＝1/3σS可知，当形成一个临界晶核时，还有1／3的表面能必须由液体中的能量起伏来提供。

液体中存在的结构起伏，是结晶时产生晶核的基础。

因此，结构起伏是结晶过程必须具备的结构条件。

2． 凝固驱动力∆G＝一3253.5J／mol。

3． 

（1）rk＝9.03X10-10m； 

（2）n=261个。

4． 所谓界面的平衡结构，是指在界面能最小的条件下，界面处于最稳定状态。

其问题实质是分析当界面粗糙化时，界面自由能的相对变化。

为此，作如下假定：

（1）   液、固相的平衡处于恒温条件下；

（2）   液、固相在界面附近结构相同；

（3）   只考虑组态熵，忽略振动嫡。

设N为液、固界面上总原子位置数，固相原子位置数为n，其占据分数为x＝n/N；界面上空位分数为1一x，空位数为N（1一x）。

形成空位引起内能和结构熵的变化，相应引起表面吉布斯自由能的变化为

形成N（1一x）个空位所增加的内能由其所断开的固态键数和一对原子的键能的乘积决定。

内能的变化为

式中ξ与晶体结构有关，称为晶体学因子。

其次，求熵变。

由熵变的定义式，则有

按striling近似式展开，当N很大时，得

∆S＝一kN[xlnx+（1一x）In（1一x）]

最后，计算液—固界面上自由能总的变化，即

所以：

令：

所以：

5． 在铸锭组织中，一般有三层晶区：

（1）最外层细晶区。

其形成是由于模壁的温度较低，液体的过冷度交大，因此形核率较高。

（2）中间为柱状晶区。

其形成是由于模壁的温度升高，晶核的成长速率大于晶核的形核率，且沿垂直于模壁风向的散热较为有利。

在细晶区中取向有利的晶粒优先生长为柱状晶粒。

（3）中心为等轴晶区。

其形成是由于模壁温度进一步升高，液体过冷度进一步降低，剩余液体的散热方向性已不明显，处于均匀冷却状态；同时，未熔杂质、破断枝晶等易集中于剩余液体中，这些都促使了等轴晶的形成。

应该指出，铸锭的组织并不是都具有3层晶区。

由于凝固条件的不同，也会形成在铸锭中只有某一种晶区，或只有某两种晶区。

6． 固态金属熔化时不一定出现过热。

如熔化时，液相若与汽相接触，当有少量液体金属在固相表面形成时，就会很快复盖在整个表面（因为液体金属总是润湿同一种固体金属），由附图2.6表面张力平衡可知

，而实验指出

，说明在熔化时，自由能的变化aG（表面）

实际金属多属于这种情况。

如果固体金属熔化时液相不与汽相接触，则有可能使固体金属过热，然而，这在实际上是难以做到的。

7． LDPE的自由空间为

；

HDPE的自由空间为

8． 金属玻璃是通过超快速冷却的方法，抑制液—固结晶过程，获得性能异常的非晶态结构。

玻璃是过冷的液体。

这种液体的黏度大，原子迁移性小，因而难于结晶，如高分子材料（硅酸盐、塑料等）在一般的冷却条件下，便可获得玻璃态。

金属则不然。

由于液态金属的黏度低，冷到液相线以下便迅速结晶，因而需要很大的冷却速度（估计>1010℃／s）才能获得玻璃态。

为了在较低的冷速下获得金属玻璃，就应增加液态的稳定性，使其能在较宽的温度范围存在。

实验证明，当液相线很陡从而有较低共晶温度时，就能增加液态的稳定性，故选用这样的二元系（如Fe—B，Fe—C，h—P，Fe—Si等）。

为了改善性能，可以加入一些其他元

素（如Ni，Mo，Cr，Co等）。

这类金属玻璃可以在10’一10‘℃／s的冷速下获得。

9． 实际结晶温度与理论结晶温度之间的温度差，称为过冷度（∆T＝Tm一Tn）。

它是相变热力学条件所要求的，只有AT>0时，才能造成固相的自由能低于液相自由能的条件，液、固相间的自由能差便是结晶的驱动力。

过冷液体中，能够形成等于临界晶核半径的晶胚时的过冷度，称为临界过冷度（∆T*）。

显然，当实际过冷度∆T<∆T*时，过冷液体中最大的晶胚尺寸也小于临界晶核半径，故难于成核；只有当∆T>∆T*时，才能均匀形核。

所以，临界过冷度是形核时所要求的。

晶核长大时，要求液—固界面前沿液体中有一定的过冷，才能满足（dN／dt）F>（dN／dt）M，这种过冷称为动态过冷度（∆Tk＝Tm一Ti），它是晶体长大的必要条件。

10．             纯金属生长形态是指晶体宏观长大时界面的形貌。

界面形貌取决于界面前沿液体中的温度分布。

（1）   平面状长大：

当液体具有正温度梯度时，晶体以平直界面方式推移长大。

此时，界面上任何偶然的、小的凸起伸入液体时，都会使其过冷度减小，长大速率降低或停止长大，而被周围部分赶上，因而能保持平直界面的推移。

长大中晶体沿平行温度梯度的方向生长，或沿散热的反方向生长，而其他方向的生长则受到抑制。

（2）   树枝状长大：

当液体具有负温度梯度时，在界面上若形成偶然的凸起伸入前沿液体时，由于前方液体有更大的过冷度，有利于晶体长大和凝固潜热的散失，从而形成枝晶的一次轴。

一个枝晶的形成，其潜热使邻近液体温度升高，过冷度降低，因此，类似的枝晶只在相邻一定间距的界面上形成，相互平行分布。

在一次枝晶处的温度比枝晶间温度要高，如附图2．7（a）中所示的AA断面上丁A>丁n，这种负温度梯度使一次轴上又长出二次轴分枝，如附图2.7（b）所示。

同样，还会产生多次分枝。

枝晶生长的最后阶段，由于凝固潜热放出，使枝晶周围的液体温度升高至熔点以上，液体中出现正温度梯度，此时晶体长大依靠平界面方式推进，直至枝晶间隙全部被填满为止。

11．             根据自由能与晶胚半径的变化关系，可以知道半径rrk的晶胚才有可能成核；而r＝rk的晶胚既可能消失，也可能稳定长大。

因此，半径为“的晶胚称为临界晶核。

其物理意义是，过冷液体中涌现出来的短程有序的原子团，当其尺寸r≥rk时，这样的原子团便可成为晶核而长大。

临界晶核半径rk，其大小与过冷度有关，则有

12．             晶体长大机制是指晶体微观长大方式，它与液—固界面结构有关。

具有粗糙界面的物质，因界面上约有50％的原子位置空着，这些空位都可接受原子，故液体原子可以单个进入空位，与晶体相连接，界面沿其法线方向垂直推移，呈连续式长大。

具有光滑界面的晶体长大，不是单个原子的附着，而是以均匀形核的方式，在晶体学小平面界面上形成一个原子层厚的二维晶核与原界面间形成台阶，单个原子可以在台阶上填充，使二维晶核侧向长大，在该层填满后，则在新的界面上形成新的二维晶核，继续填满，如此反复进行。

若晶体的光滑界面存在有螺型位错的露头，则该界面成为螺旋面，并形成永不消失的台阶，原子附着到台阶上使晶体长大。

13．             形成单晶体的基本条件是使液体金属结晶时只产生一个核心（或只有一个核心能够长大）并长大成单晶体。

14．             

（1）……在冷却曲线上出现的实际结晶温度与熔点之差……液-固界面前沿液态中的温度与熔点之差。

（2）……使体系自由能减小……

（3）在过冷液体中，液态金属中出现的……

（4）在一定过冷度（>厶了’）下……

（5）……就是体系自由能的减少能够补偿2／3表面自由能……

（6）……不能成核，即便是有足够的能量起伏提供，还是不能成核。

（7）测定某纯金属均匀形核时的有效过冷度……

（8）……那么总的形核率N＝N2。

（9）……则结晶后就可以形成数万颗晶粒。

（10）……非均匀形核的形核功最小。

（11）……则只要在工艺上采取对厚处加快冷却（如加冷铁）就可以满足。

（12）……因为前者是以外加质点为基底，形核功小……

（13）……主要寻找那些熔点高，且……

（14）……若液—固界面呈粗糙型，则其液相原子……

（15）只有在负温度梯度条件下，常用纯金属……

（16）……结晶终了时的组织形态不同，前者呈树枝晶（枝间是水），后者呈一个个（块状）晶粒。

（17）……生长过程，但可以通．过实验方法，如把正在结晶的金属剩余液体倒掉，或者整体淬火等进行观察，所以关于树枝状生长形态不是一种推理。

（18）……其生长形态不会发生改变。

（19）……其界面是粗糙型的。

（20）……平直的称为粗糙界面结构……锯齿形的称为平滑界面结构。

（21）……因还与液—固界面的结构有关，即与该金属的熔化熵有关。

（22）……增加，但因金属的过冷能力小，故不会超过某一极大值……

（23）……动态过冷度比形核所需要的临界过冷度小。

1.       wMg=0.0456。

2.       

。

3.       设纯溶剂组元A的熔点为TA，液相线与固相线近似为直线，则离界面距离x处液相线温度TL为：

但在x处液相的实际温度T如附图2.8所示，应为：

因为溶质分布而产生的成分过冷为：

令

，得：

将（4）代入（3）得：

4.       C1合金成分为wMg＝0.873，wNi＝0.127；

C2合金成分为wMg＝0.66，wNi＝0.368

5.       

（1）高温区水平线为包晶线，包晶反应：

Lj+δk→αn

   中温区水平线为共晶线，共晶反应：

Ld′→αg+βh

（2）各区域组织组成物如图4—30中所示。

 （3）I合金的冷却曲线和结晶过程如附图2.9所示。

   1～2，均匀的液相L。

   2～3匀晶转变，L→δ不断结晶出δ相。

   3～3′，发生包品反应L+δ→α。

   3′～4，剩余液相继续结晶为α。

   4，凝固完成，全部为α。

   4～5，为单一α相，无变化。

   5～6，发生脱溶转变α→βII。

室温下的组织为α+βII。

   II合金的冷却曲线和结晶过程如附图2.10所示。

   1～2，均匀的液相L。

   2～3，结晶出α初，随温度下降α相不断析出，液相不断减少。

   3～3′，剩余液相发生共晶转变L→α+β。

   3′～4，α→βII，β→αII，室温下的组织为。

α初+（α+β）共+βII

 （4）室温时，合金I、II组织组成物的相对量可由杠杆定律求得。

 合金I：

 合金II：

9． 此说法不正确。

固体中的宏观扩散流不是单个原子定向跳动的结果，扩散激活能也不是单个原子迁：

移时每一次跳动需越过的能垒，固体中原子的跳动具有随机性质，扩散流是固体中扩散物质质点（如原子，离子）随机跳动的统计结果的宏观体现，当晶体中的扩散以空位机制进行时，晶体中任何一个原子在两个平衡位置之间发生跳动必须同时满足两个条件：

（2）   该原子具有的能量必须高于某一临界值∆Gf，即原子跳动激活能，以克服阻碍跳动的阻力；

（3）   该原子相邻平衡位置上存在空位。

根据统计热力学理论，在给定温度T下，晶体中任一原子的能量高于∆Gf的几率Pf，即晶体中能量高于∆Gf的原子所占原子百分数为

而晶体中的平衡空位浓度Cv，即任一原子平衡位置出现空位的几率Pv，为

显然，某一瞬间晶体中原子发生一次跳动的几率为

P也等于该瞬间发生跳动原子所占的原子百分数。

其中Q＝∆Gf＋∆Gv，就是空位扩散机制的扩散激活能。

11．             因α-Fe中的最大碳熔解度（质量分数）只有0.0218％，对于含碳质量分数大于0.0218％的钢铁在渗碳时零件中的碳浓度梯度为零，渗碳无法进行，即使是纯铁，在α相区渗碳时铁中浓度梯度很小，在表也不能获得高含碳层；另外，由于温度低，扩散系数也很小，渗碳过程极慢，没有实际意义。

γ-Fe中的碳固溶度高，渗碳时在表层可获得较高的碳浓度梯度使渗碳顺利进行。

12．             原因是。

α-Fe中的扩散系数较γ-Fe中的扩散系数高。

13．             转折点向低温方向移动。

14．             三元系扩散层内不可能存在三相共存区，但可以存在两相共存区。

原因如下：

三元系中若出现三相平衡共存，其二相中成分一定且不同相中同一组分的化学位相等，化学位梯度为零，扩散不可能发生。

三元系在两相共