数学建模程序必用.docx

数学建模程序必用.docx

《数学建模程序必用.docx》由会员分享，可在线阅读，更多相关《数学建模程序必用.docx（17页珍藏版）》请在冰豆网上搜索。

数学建模程序必用

图论算法及其MATLAB程序代码

求赋权图G=（V,E,F）中任意两点间的最短路的Warshall-Floyd算法：

设A=（aij）n×n为赋权图G=（V,E,F）的矩阵,当vivj∈E时aij=F（vivj）,否则取aii=0,aij

=+∞（i≠j）,dij表示从vi到vj点的距离,rij表示从vi到vj点的最短路中一个点的编号.

①赋初值.对所有i,j,dij=aij,rij=j.k=1.转向②

②更新dij,rij.对所有i,j,若dik+dkj＜dij,则令dij=dik+dkj,rij=k,转向③.

③终止判断.若dii＜0,则存在一条含有顶点vi的负回路,终止;或者k=n终止;否则

令k=k+1,转向②.

最短路线可由rij得到.

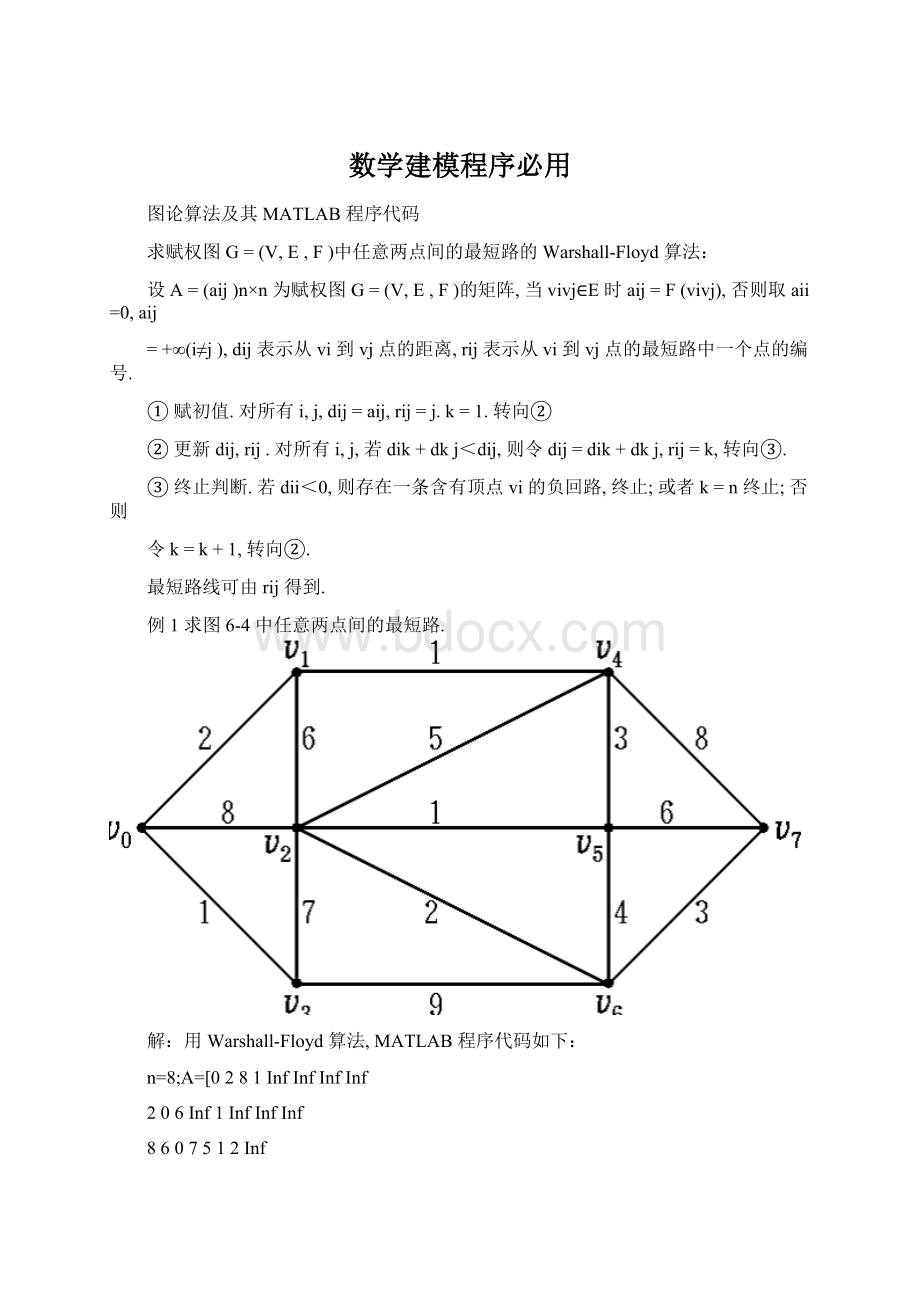
例1求图6-4中任意两点间的最短路.

解：

用Warshall-Floyd算法,MATLAB程序代码如下：

n=8;A=[0281InfInfInfInf

206Inf1InfInfInf

8607512Inf

1Inf70InfInf9Inf

Inf15Inf03Inf8

InfInf1Inf3046

InfInf29Inf403

InfInfInfInf8630];%MATLAB中,Inf表示∞

D=A;%赋初值

for（i=1:

n）for（j=1:

n）R（i,j）=j;end;end%赋路径初值

for（k=1:

n）for（i=1:

n）for（j=1:

n）if（D（i,k）+D（k,j）

R（i,j）=k;end;end;end%更新rij

k%显示迭代步数

D%显示每步迭代后的路长

R%显示每步迭代后的路径

pd=0;fori=1:

n%含有负权时

if（D（i,i）<0）pd=1;break;end;end%存在一条含有顶点vi的负回路

if（pd）break;end%存在一条负回路,终止程序

end%程序结束

图6-4

Kruskal避圈法：

将图G中的边按权数从小到大逐条考察,按不构成圈的原则加入到T

中（若有选择时,不同的选择可能会导致最后生成树的权数不同）,直到q（T）=p（G）-1为

止,即T的边数=G的顶点数-1为止.

Kruskal避圈法的MATLAB程序代码如下：

n=8;A=[02810000

20601000

86075120

10700090

01500308

00103046

00290403

00008630];

k=1;%记录A中不同正数的个数

for（i=1:

n-1）for（j=i+1:

n）%此循环是查找A中所有不同的正数

if（A（i,j）>0）x（k）=A（i,j）;%数组x记录A中不同的正数

kk=1;%临时变量

for（s=1:

k-1）if（x（k）==x（s））kk=0;break;end;end%排除相同的正数

k=k+kk;end;end;end

k=k-1%显示A中所有不同正数的个数

for（i=1:

k-1）for（j=i+1:

k）%将x中不同的正数从小到大排序

if（x（j）

T（n,n）=0;%将矩阵T中所有的元素赋值为0

q=0;%记录加入到树T中的边数

for（s=1:

k）if（q==n）break;end%获得最小生成树T,算法终止

for（i=1:

n-1）for（j=i+1:

n）if（A（i,j）==x（s））T（i,j）=x（s）;T（j,i）=x（s）;%加入边到树T中

TT=T;%临时记录T

while

（1）pd=1;%砍掉TT中所有的树枝

for（y=1:

n）kk=0;

for（z=1:

n）if（TT（y,z）>0）kk=kk+1;zz=z;end;end%寻找TT中的树枝

if（kk==1）TT（y,zz）=0;TT（zz,y）=0;pd=0;end;end%砍掉TT中的树枝

if（pd）break;end;end%已砍掉了TT中所有的树枝

pd=0;%判断TT中是否有圈

for（y=1:

n-1）for（z=y+1:

n）if（TT（y,z）>0）pd=1;break;end;end;end

if（pd）T（i,j）=0;T（j,i）=0;%假如TT中有圈

elseq=q+1;end;end;end;end;end

T%显示近似最小生成树T,程序结束

求二部图G的最大匹配的算法（匈牙利算法）,其基本思想是：

从G的任意匹配M开始,

对X中所有M的非饱和点,寻找M-增广路.若不存在M-增广路,则M为最大匹配;若存

在M-增广路P,则将P中M与非M的边互换得到比M多一边的匹配M1,再对M1重复上

述过程.

设G=（X,Y,E）为二部图,其中X={x1,x2,⋯,xn},Y={y1,y2,⋯,yn}.任取G的一初

始匹配M（如任取e∈E,则M={e}是一个匹配）.

①令S=f,T=f,转向②.

②若M饱和X\S的所有点,则M是二部图G的最大匹配.否则,任取M的非饱和点

u∈X\S,令S=S∪{u},转向③.

③记N（S）={v|u∈S,uv∈E}.若N（S）=T,转向②.否则取y∈N（S）\T.若y是M

的饱和点,转向④,否则转向⑤.

④设xy∈M,则令S=S∪{x},T=T∪{y},转向③.

⑤u-y路是M-增广路,设为P,并令M=M⊕P,转向①.这里M⊕P=M∪P\M∩

P,是对称差.

由于计算M-增广路P比较麻烦,因此将迭代步骤改为：

①将X中M的所有非饱和点（不是M中某条边的端点）都给以标号0和标记*,转向②.

②若X中所有有标号的点都已去掉了标记*,则M是G的最大匹配.否则任取X中一

个既有标号又有标记*的点xi,去掉xi的标记*,转向③.

③找出在G中所有与xi邻接的点yj（即xiyj∈E）,若所有这样的yj都已有标号,则转向

②,否则转向④.

④对与xi邻接且尚未给标号的yj都给定标号i.若所有的yj都是M的饱和点,则转向⑤,

否则逆向返回.即由其中M的任一个非饱和点yj的标号i找到xi,再由xi的标号k找到yk,⋯,

最后由yt的标号s找到标号为0的xs时结束,获得M-增广路xsyt⋯xiyj,记P={xsyt,⋯,

xiyj},重新记M为M⊕P,转向①.

⑤将yj在M中与之邻接的点xk（即xkyj∈M）,给以标号j和标记*,转向②.

例1求图6-9中所示的二部图G的最大匹配.

匈牙利算法的MATLAB程序代码如下：

m=5;n=5;A=[01100

11011

01100

01100

00011];

M（m,n）=0;

for（i=1:

m）for（j=1:

n）if（A（i,j））M（i,j）=1;break;end;end%求初始匹配M

if（M（i,j））break;end;end%获得仅含一条边的初始匹配M

while

（1）

for（i=1:

m）x（i）=0;end%将记录X中点的标号和标记*

for（i=1:

n）y（i）=0;end%将记录Y中点的标号和标记*

for（i=1:

m）pd=1;%寻找X中M的所有非饱和点

for（j=1:

n）if（M（i,j））pd=0;end;end

if（pd）x（i）=-n-1;end;end%将X中M的所有非饱和点都给以标号0和标记*,程序中用n+1表

示0标号,标号为负数时表示标记*

pd=0;

while

（1）xi=0;

for（i=1:

m）if（x（i）<0）xi=i;break;end;end%假如X中存在一个既有标号又有标记*的点,则任

取X中一个既有标号又有标记*的点xi

if（xi==0）pd=1;break;end%假如X中所有有标号的点都已去掉了标记*,算法终止

x（xi）=x（xi）*（-1）;%去掉xi的标记*

k=1;

for（j=1:

n）if（A（xi,j）&y（j）==0）y（j）=xi;yy（k）=j;k=k+1;end;end%对与xi邻接且尚未给标号的yj都

给以标号i

if（k>1）k=k-1;

for（j=1:

k）pdd=1;

for（i=1:

m）if（M（i,yy（j）））x（i）=-yy（j）;pdd=0;break;end;end%将yj在M中与之邻接的

点xk（即xkyj∈M）,给以标号j和标记*

if（pdd）break;end;end

if（pdd）k=1;j=yy（j）;%yj不是M的饱和点

while

（1）P（k,2）=j;P（k,1）=y（j）;j=abs（x（y（j）））;%任取M的一个非饱和点yj,逆向返回

if（j==n+1）break;end%找到X中标号为0的点时结束,获得M-增广路P

k=k+1;end

for（i=1:

k）if（M（P（i,1）,P（i,2）））M（P（i,1）,P（i,2））=0;%将匹配M在增广路P中出现的边

去掉

elseM（P（i,1）,P（i,2））=1;end;end%将增广路P中没有在匹配M中出现的边加入

到匹配M中

break;end;end;end

if（pd）break;end;end%假如X中所有有标号的点都已去掉了标记*,算法终止

M%显示最大匹配M,程序结束

图6-9

利用可行点标记求最佳匹配的算法步骤如下：

设G=（X,Y,E,F）为完备的二部赋权图,L是其一个初始可行点标记,通常取

.

（）0,

（）max{（）|},

yY

xX

Ly

LxFxyyY

∈

∈

⎩⎨⎧

=

=∈

M是GL的一个匹配.

①若X的每个点都是M的饱和点,则M是最佳匹配.否则取M的非饱和点u∈X,令S

={u},T=f,转向②.

②记NL（S）={v|u∈S,uv∈EL}.若NL（S）=T,则GL没有完美匹配,转向③.否则转

向④.

③调整可行点标记,计算

aL=min{L（x）+L（y）-F（xy）|x∈S,y∈Y\T}.

由此得新的可行顶点标记

H（v）=,

（）,

（）,

（）,

vT

vS

Lv

Lva

Lva

L

L

∈

∈

⎪⎩

⎪⎨

⎧

+

-

令L=H,GL=GH,重新给出GL的一个匹配M,转向①.

④取y∈NL（S）\T,若y是M的饱和点,转向⑤.否则,转向⑥.

⑤设xy∈M,则令S=S∪{x},T=T∪{y},转向②.

⑥在GL中的u-y路是M-增广路,记为P,并令M=M⊕P,转向①.

利用可行点标记求最佳匹配算法的MATLAB程序代码如下：

n=4;A=[4551

2246

4233

5021];

for（i=1:

n）L（i,1）=0;L（i,2）=0;end

for（i=1:

n）for（j=1:

n）if（L（i,1）

M（i,j）=0;end;end

for（i=1:

n）for（j=1:

n）%生成子图Gl

if（L（i,1）+L（j,2）==A（i,j））Gl（i,j）=1;

elseGl（i,j）=0;end;end;end

ii=0;jj=0;

for（i=1:

n）for（j=1:

n）if（Gl（i,j））ii=i;jj=j;break;end;end

if（ii）break;end;end%获得仅含Gl的一条边的初始匹配M

M（ii,jj）=1;

for（i=1:

n）S（i）=0;T（i）=0;NlS（i）=0;end

while

（1）

for（i=1:

n）k=1;

否则.

for（j=1:

n）if（M（i,j））k=0;break;end;end

if（k）break;end;end

if（k==0）break;end%获得最佳匹配M,算法终止

S

（1）=i;jss=1;jst=0;%S={xi},T=φ

while

（1）

jsn=0;

for（i=1:

jss）for（j=1:

n）if（Gl（S（i）,j））jsn=jsn+1;NlS（jsn）=j;%NL（S）={v|u∈S,uv∈EL}

for（k=1:

jsn-1）if（NlS（k）==j）jsn=jsn-1;end;end;end;end;end

if（jsn==jst）pd=1;%判断NL（S）=T?

for（j=1:

jsn）if（NlS（j）~=T（j））pd=0;break;end;end;end

if（jsn==jst&pd）al=Inf;%如果NL（S）=T,计算al,Inf为∞

for（i=1:

jss）for（j=1:

n）pd=1;

for（k=1:

jst）if（T（k）==j）pd=0;break;end;end

if（pd&al>L（S（i）,1）+L（j,2）-A（S（i）,j））al=L（S（i）,1）+L（j,2）-A（S（i）,j）;end;end;end

for（i=1:

jss）L（S（i）,1）=L（S（i）,1）-al;end%调整可行点标记

for（j=1:

jst）L（T（j）,2）=L（T（j）,2）+al;end%调整可行点标记

for（i=1:

n）for（j=1:

n）%生成子图GL

if（L（i,1）+L（j,2）==A（i,j））Gl（i,j）=1;

elseGl（i,j）=0;end

M（i,j）=0;k=0;end;end

ii=0;jj=0;

for（i=1:

n）for（j=1:

n）if（Gl（i,j））ii=i;jj=j;break;end;end

if（ii）break;end;end%获得仅含Gl的一条边的初始匹配M

M（ii,jj）=1;break

else%NL（S）≠T

for（j=1:

jsn）pd=1;%取y∈NL（S）\T

for（k=1:

jst）if（T（k）==NlS（j））pd=0;break;end;end

if（pd）jj=j;break;end;end

pd=0;%判断y是否为M的饱和点

for（i=1:

n）if（M（i,NlS（jj）））pd=1;ii=i;break;end;end

if（pd）jss=jss+1;S（jss）=ii;jst=jst+1;T（jst）=NlS（jj）;%S=S∪{x},T=T∪{y}

else%获得Gl的一条M-增广路,调整匹配M

for（k=1:

jst）M（S（k）,T（k））=1;M（S（k+1）,T（k））=0;end

if（jst==0）k=0;end

M（S（k+1）,NlS（jj））=1;break;end;end;end;end

MaxZjpp=0;

for（i=1:

n）for（j=1:

n）if（M（i,j））MaxZjpp=MaxZjpp+A（i,j）;end;end;end

M%显示最佳匹配M

MaxZjpp%显示最佳匹配M的权,程序结束

从一个可行流f开始,求最大流的Ford--Fulkerson标号算法的基本步骤：

⑴标号过程

①给发点vs以标号（+,+∞）,ds=+∞.

②选择一个已标号的点x,对于x的所有未给标号的邻接点y,按下列规则处理：

当yx∈E,且fyx＞0时,令dy=min{fyx,dx},并给y以标号（x-,dy）.

当xy∈E,且fxy＜Cxy时,令dy=min{Cxy-fxy,dx},并给y以标号（x+,dy）.

③重复②直到收点vt被标号或不再有点可标号时为止.若vt得到标号,说明存在一条

可增广链,转⑵调整过程;若vt未得到标号,标号过程已无法进行时,说明f已经是最大流.

⑵调整过程

④决定调整量d=dvt,令u=vt.

⑤若u点标号为（v+,du）,则以fvu+d代替fvu;若u点标号为（v-,du）,则以fvu-d

代替fvu.

⑥若v=vs,则去掉所有标号转⑴重新标号;否则令u=v,转⑤.

算法终止后,令已有标号的点集为S,则割集（S,Sc）为最小割,从而Wf=C（S,Sc）.

例1求图6-19所示网络的最大流.

利用Ford--Fulkerson标号法求最大流算法的MATLAB程序代码如下：

n=8;C=[05430000

00005300

00000320

00000020

00000004

00000003

00000005

00000000];%弧容量

for（i=1:

n）for（j=1:

n）f（i,j）=0;end;end%取初始可行流f为零流

for（i=1:

n）No（i）=0;d（i）=0;end%No,d记录标号

图6-19

while

（1）

No

（1）=n+1;d

（1）=Inf;%给发点vs标号

while

（1）pd=1;%标号过程

for（i=1:

n）if（No（i））%选择一个已标号的点vi

for（j=1:

n）if（No（j）==0&f（i,j）

No（j）=i;d（j）=C（i,j）-f（i,j）;pd=0;

if（d（j）>d（i））d（j）=d（i）;end

elseif（No（j）==0&f（j,i）>0）%对于未给标号的点vj,当vjvi为非零流弧时

No（j）=-i;d（j）=f（j,i）;pd=0;

if（d（j）>d（i））d（j）=d（i）;end;end;end;end;end

if（No（n）|pd）break;end;end%若收点vt得到标号或者无法标号,终止标号过程

if（pd）break;end%vt未得到标号,f已是最大流,算法终止

dvt=d（n）;t=n;%进入调整过程,dvt表示调整量

while

（1）

if（No（t）>0）f（No（t）,t）=f（No（t）,t）+dvt;%前向弧调整

elseif（No（t）<0）f（No（t）,t）=f（No（t）,t）-dvt;end%后向弧调整

if（No（t）==1）for（i=1:

n）No（i）=0;d（i）=0;end;break;end%当t的标号为vs时,终止调整过程

t=No（t）;end;end;%继续调整前一段弧上的流f

wf=0;for（j=1:

n）wf=wf+f（1,j）;end%计算最大流量

f%显示最大流

wf%显示最大流量

No%显示标号,由此可得最小割,程序结束

设网络G=（V,E,C）,取初始可行流f为零流,求解最小费用流问题的迭代步骤：

①构造有向赋权图Gf=（V,Ef,F）,对于任意的vivj∈E,Ef,F的定义如下：

当fij=0时,vivj∈Ef,F（vivj）=bij;

当fij=Cij时,vjvi∈Ef,F（vjvi）=-bij;

当0＜fij＜Cij时,vivj∈Ef,F（vivj）=bij,vjvi∈Ef,F（vjvi）=-bij.

转向②.

②求出有向赋权图Gf=（V,Ef,F）中发点vs到收点vt的最短路m,若最短路m存在转向

③;否则f是所求的最小费用最大流,停止.

③增流.同求最大流的方法一样,重述如下：

令

.

-

+

∈

∈

⎪⎩

⎪⎨⎧

-

=

m

m

d

ij

ij

ij

ijij

ijvv

vv

f

Cf

d=min{dij|vivj∈m},重新定义流f={fij}为

fij=,

-

+

∈

∈

⎪⎩

⎪⎨

⎧

-

+

m

m

d

d

ij

ij

ij

ij

ij

vv

vv

f

f

f

如果Wf大于或等于预定的流量值,则适当减少d值,使Wf等于预定的流量值,那么f是所

求的最小费用流,停止;否则转向①.

求解含有负权的有向赋权图G=（V,E,F）中某一点到其它各点最短路的Ford算法.

当vivj∈E时记wij=F（vivj）,否则取wii=0,wij=+∞（i≠j）.v1到vi的最短路长记为p（i）,

v1到vi的最短路中vi的前一个点记为q（i）.Ford算法的迭代步骤：

①赋初值p

（1）=0,p（i）=+∞,q（i）=i,i=2,3,⋯,n.

②更新p（i）,q（i）.对于i=2,3,⋯,n和j=1,2,⋯,n,如果p（i）＜p（j）+wji,则令

p（i）=p（j）,q（i）=j.

③终止判断：

若所有的p（i）都无变化,停止;否则转向②.

在算法的每一步中,p（i）都是从v1到vi的最短路长度的上界.若不存在负长回路,则从

v1到vi的最短路长度是p（i）的下界,经过n-1次迭代后p（