 TSP的遗传算法程序实验报告.docx
TSP的遗传算法程序实验报告.docx
- 文档编号:6217682
- 上传时间:2023-01-04
- 格式:DOCX
- 页数:12
- 大小:63.05KB
TSP的遗传算法程序实验报告.docx
《TSP的遗传算法程序实验报告.docx》由会员分享,可在线阅读,更多相关《TSP的遗传算法程序实验报告.docx(12页珍藏版)》请在冰豆网上搜索。
TSP的遗传算法程序实验报告
TSP的遗传算法程序
一、实验原理
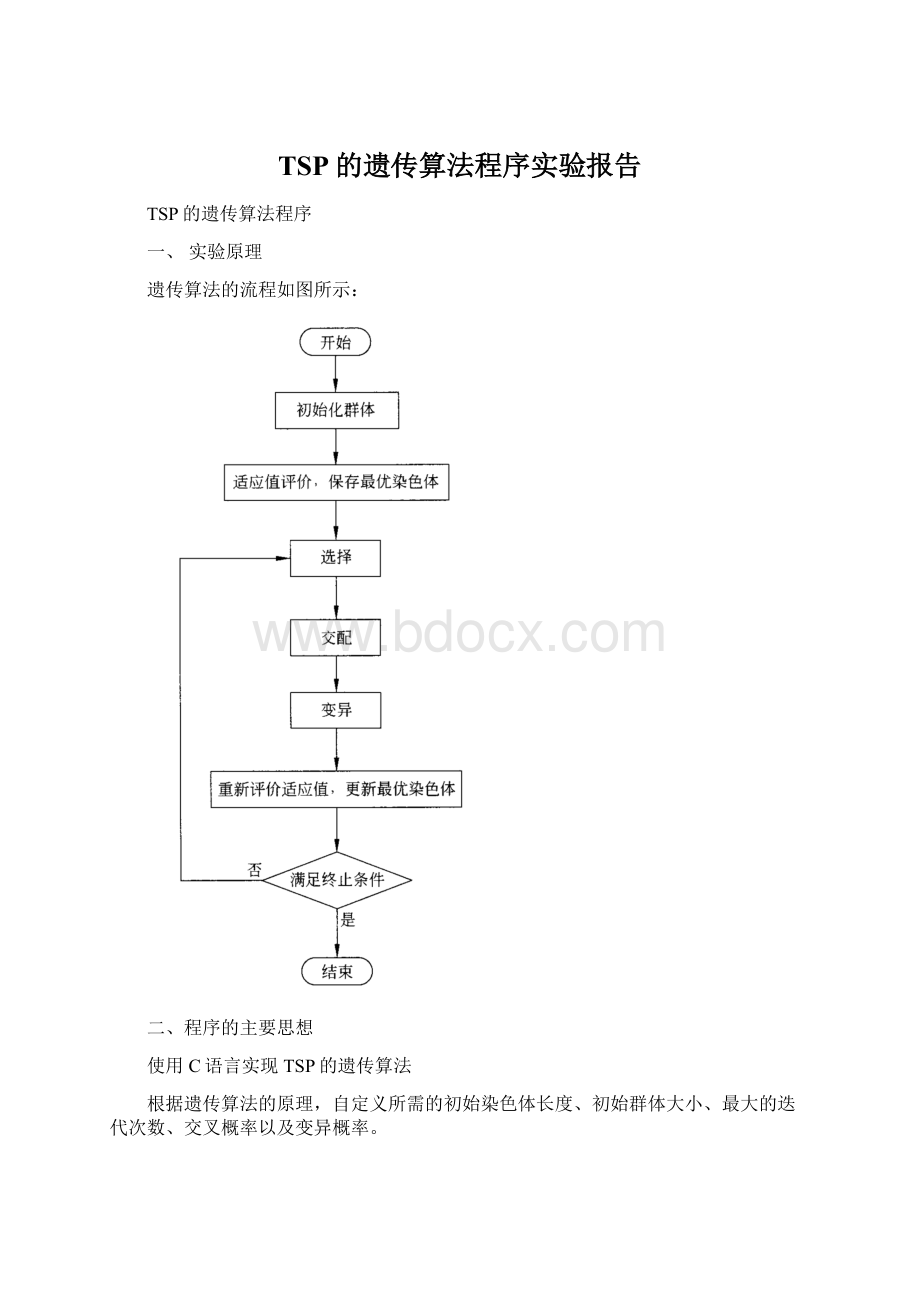
遗传算法的流程如图所示:
二、程序的主要思想
使用C语言实现TSP的遗传算法
根据遗传算法的原理,自定义所需的初始染色体长度、初始群体大小、最大的迭代次数、交叉概率以及变异概率。
初始时生成与染色体长度相同个数的城市,为每个城市随机生成平面坐标,将城市的初始生成的顺序作为初始的路径,即第一条染色体。
计算路径中相邻城市之间的距离,并进行保存。
将生成的城市再进行多次的重新排列,得到多条不同的路径,将这些路径作为初始群体里的染色体,计算每条路径的长度。
通过自定义的适应度函数计算染色体的适应度,通过交叉、变异生成新的种群。
对新种群继续迭代操作,直到达到初始定义的迭代次数,获得最终的路径及路径图。
三、程序的主要步骤
①染色体初始化的子函数
1)voidinitialize()
2){intk,j,minx,miny,maxx,maxy;
3)initdata();
4)minx=0;
5)miny=0;
6)maxx=0;maxy=0;
7)for(k=0;k 8){x[k]=rand(); 9)if(x[k]>maxx)maxx=x[k]; 10)if(x[k] 11)y[k]=rand(); 12)if(y[k]>maxy)maxy=y[k]; 13)if(y[k] 14)} 15)if((maxx-minx)>(maxy-miny)) 16){maxxy=maxx-minx;} 17)else{maxxy=maxy-miny;} 18)maxdd=0.0; 19)for(k=0;k 20)for(j=0;j 21){dd[k*lchrom+j]=hypot(x[k]-x[j],y[k]-y[j]); 22)if(maxdd 23)} 24)refpd=dd[lchrom-1]; 25)for(k=0;k 26)refpd=refpd+dd[k*lchrom+k+2]; 27)for(j=0;j 28)dd[j*lchrom+j]=4.0*maxdd; 29)ff=(0.765*maxxy*pow(lchrom,0.5)); 30)minpp=0; 31)min=dd[lchrom-1]; 32)for(j=0;j 33){if(dd[lchrom*j+lchrom-1] 34){min=dd[lchrom*j+lchrom-1]; 35)minpp=j; 36)} 37)} 38)initpop(); 39)statistics(oldpop); 40)initreport(); 41)} 7)for(k=0;k 8){x[k]=rand(); 9)if(x[k]>maxx)maxx=x[k]; 10)if(x[k] 11)y[k]=rand(); 12)if(y[k]>maxy)maxy=y[k] 13)if(y[k] 14)} 此段程序是初始化多个城市的坐标值(x,y),其中(x[k],y[k])代表第k+1个城市的坐标值,也相当于初始染色体的第k+1个基因值。 19)for(k=0;k 20)for(j=0;j 21){dd[k*lchrom+j]=hypot(x[k]-x[j],y[k]-y[j]); 此段程序是将初始生成的城市的顺序做为第一条路径的顺序,计算路径中相邻点之间的距离。 ②群体初始化的子函数 1)voidinitpop() 2){unsignedcharj1; 3)unsignedintk5,i1,i2,j,i,k,j2,j3,j4,p5[maxstring]; 4)floatf1,f2; 5)j=0; 6)for(k=0;k 7)oldpop[j].chrom[k]=k; 8)for(k=0;k 9)p5[k]=oldpop[j].chrom[k]; 10)randomize(); 11)for(;j 12){j2=random(lchrom); 13)for(k=0;k 14){j3=random(lchrom); 15)j4=random(lchrom); 16)j1=p5[j3]; 17)p5[j3]=p5[j4]; 18)p5[j4]=j1; 19)} 20)for(k=0;k 21)oldpop[j].chrom[k]=p5[k]; 22)} 23)for(k=0;k 24)for(j=0;j 25)dd[k*lchrom+j]=hypot(x[k]-x[j],y[k]-y[j]); 26)for(j=0;j 27){oldpop[j].x=(float)decode(oldpop[j].chrom); 28)oldpop[j].fitness=objfunc(oldpop[j].x); 29)oldpop[j].parent1=0; 30)oldpop[j].parent2=0; 31)oldpop[j].xsite=0; 32)} 33)} 6)for(k=0;k 7)oldpop[j].chrom[k]=k; 此段程序是为最初生成的第一条染色体中城市进行编号,之后的得到的染色体都是对这些编号进行重新的排序。 11)for(;j 12){j2=random(lchrom); 13)for(k=0;k 14){j3=random(lchrom); 15)j4=random(lchrom); 16)j1=p5[j3]; 17)p5[j3]=p5[j4]; 18)p5[j4]=j1; 19)} 20)for(k=0;k 21)oldpop[j].chrom[k]=p5[k]; 22)} 此段程序是将初始的染色体中的基因即路径的城市进行重新的排列,得到多个染色体,将这染色体组合成为初始群体---第0代群体。 ③计算适应度子函数以及适应度统计子函数 floatobjfunc(floatx1) {floaty; y=100.0*ff/x1; returny; } /*&&&&&&&&&&&&&&&&&&&*/ voidstatistics(pop) structpp*pop; {intj; sumfitness=pop[0].fitness; min=pop[0].fitness; max=pop[0].fitness; maxpp=0; minpp=0; for(j=1;j {sumfitness=sumfitness+pop[j].fitness; if(pop[j].fitness>max) {max=pop[j].fitness; maxpp=j; } if(pop[j].fitness {min=pop[j].fitness; minpp=j; } } avg=sumfitness/(float)popsize; } 根据自定义的适应度函数,统计初始群体中每个染色体的适应度 ④群体更新子函数 voidgeneration() {unsignedintk,j,j1,j2,i1,i2,mate1,mate2; floatf1,f2; j=0; do{ mate1=select(); pp: mate2=select(); if(mate1==mate2)gotopp; crossover(oldpop[mate1].chrom,oldpop[mate2].chrom,j); newpop[j].x=(float)decode(newpop[j].chrom); newpop[j].fitness=objfunc(newpop[j].x); newpop[j].parent1=mate1; newpop[j].parent2=mate2; newpop[j].xsite=jcross; newpop[j+1].x=(float)decode(newpop[j+1].chrom); newpop[j+1].fitness=objfunc(newpop[j+1].x); newpop[j+1].parent1=mate1; newpop[j+1].parent2=mate2; newpop[j+1].xsite=jcross; if(newpop[j].fitness>min) {for(k=0;k oldpop[minpp].chrom[k]=newpop[j].chrom[k]; oldpop[minpp].x=newpop[j].x; oldpop[minpp].fitness=newpop[j].fitness; co_min++; return; } if(newpop[j+1].fitness>min) {for(k=0;k oldpop[minpp].chrom[k]=newpop[j+1].chrom[k]; oldpop[minpp].x=newpop[j+1].x; oldpop[minpp].fitness=newpop[j+1].fitness; co_min++; return; } j=j+2; }while(j } 利用第0代群体中的染色体的适应度值进行选择,得到下一代种群中的染色体。 ⑤染色体的交叉和变异 intcrossover(unsignedchar*parent1,unsignedchar*parent2,intk5) {intk,j,mutate,i1,i2,j5; intj1,j2,j3,s0,s1,s2; unsignedcharjj,ts1[maxstring],ts2[maxstring]; floatf1,f2; s0=0;s1=0;s2=0; if(flip(pcross)) {jcross=random(lchrom-1); j5=random(lchrom-1); ncross=ncross+1; if(jcross>j5){k=jcross;jcross=j5;j5=k;} } elsejcross=lchrom; if(jcross! =lchrom) {s0=1; k=0; for(j=jcross;j {ts1[k]=parent1[j]; ts2[k]=parent2[j]; k++; } j3=k; for(j=0;j {j2=0; while((parent2[j]! =ts1[j2])&&(j2 if(j2==k) {ts1[j3]=parent2[j]; j3++; } } j3=k; for(j=0;j {j2=0; while((parent1[j]! =ts2[j2])&&(j2 if(j2==k) {ts2[j3]=parent1[j]; j3++; } } for(j=0;j {newpop[k5].chrom[j]=ts1[j]; newpop[k5+1].chrom[j]=ts2[j]; } } else {for(j=0;j {newpop[k5].chrom[j]=parent1[j]; newpop[k5+1].chrom[j]=parent2[j]; } mutate=flip(pmutation); if(mutate) {s1=1; nmutation=nmutation+1; for(j3=0;j3<200;j3++) {j1=random(lchrom); j=random(lchrom); jj=newpop[k5].chrom[j]; newpop[k5].chrom[j]=newpop[k5].chrom[j1]; newpop[k5].chrom[j1]=jj; } } mutate=flip(pmutation); if(mutate) {s2=1; nmutation=nmutation+1; for(j3=0;j3<100;j3++) {j1=random(lchrom); j=random(lchrom); jj=newpop[k5+1].chrom[j]; newpop[k5+1].chrom[j]=newpop[k5+1].chrom[j1]; newpop[k5+1].chrom[j1]=jj; } } } j2=random(2*lchrom/3); for(j=j2;j for(k=0;k {if(k==j)continue; if(k>j){i2=k;i1=j;} else{i1=k;i2=j;} f1=dd[lchrom*newpop[k5].chrom[i1]+newpop[k5].chrom[i2]]; f1=f1+dd[lchrom*newpop[k5].chrom[(i1+1)%lchrom]+ newpop[k5].chrom[(i2+1)%lchrom]]; f2=dd[lchrom*newpop[k5].chrom[i1]+ newpop[k5].chrom[(i1+1)%lchrom]]; f2=f2+dd[lchrom*newpop[k5].chrom[i2]+ newpop[k5].chrom[(i2+1)%lchrom]]; if(f1 } j2=random(2*lchrom/3); for(j=j2;j for(k=0;k {if(k==j)continue; if(k>j){i2=k;i1=j;} else{i1=k;i2=j;} f1=dd[lchrom*newpop[k5+1].chrom[i1]+newpop[k5+1].chrom[i2]]; f1=f1+dd[lchrom*newpop[k5+1].chrom[(i1+1)%lchrom]+ newpop[k5+1].chrom[(i2+1)%lchrom]]; f2=dd[lchrom*newpop[k5+1].chrom[i1]+ newpop[k5+1].chrom[(i1+1)%lchrom]]; f2=f2+dd[lchrom*newpop[k5+1].chrom[i2]+ newpop[k5+1].chrom[(i2+1)%lchrom]]; if(f1 } return1; } 根据初始定义的交叉和变异概率,对从旧群体中选择出的染色体进行交叉和变异。 将交叉或变异而生成的新染色体以及不需要交叉或变异的染色体传到群体更新子函数中,得到新种群。 通过不断的对旧群体进行染色体选择、交叉和变异的迭代操作,直到到达初始定义的迭代次数。 最终得到的路径为近似最优的路径。 此路径的长度是所有最初生成的所有路径中最短的路径。 四、程序结果 输入要保存结果的文件的文件名; 进行初始化: Popsize: 群体的规模 Chromlength: 染色体的长度,即城市的个数 Maxgenerations: 最大的迭代次数 Crossoverprobability: 染色体的交叉概率 Mutationprobability: 染色体的变异概率 最终结果: 生成一个TSP文件,此文件中记录了初始化时每个城市的坐标(x,y),并且记录了最终选择的最优路径。 (由于无法截图最终结果图,所以此处略过最终显示的路径图)
- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- TSP 遗传 算法 程序 实验 报告
 冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。


 铝散热器项目年度预算报告.docx
铝散热器项目年度预算报告.docx
