 学年苏科版八年级数学初二上册第一章全等三角形单元测试含答案.docx
学年苏科版八年级数学初二上册第一章全等三角形单元测试含答案.docx
- 文档编号:616645
- 上传时间:2022-10-11
- 格式:DOCX
- 页数:23
- 大小:152.23KB
学年苏科版八年级数学初二上册第一章全等三角形单元测试含答案.docx
《学年苏科版八年级数学初二上册第一章全等三角形单元测试含答案.docx》由会员分享,可在线阅读,更多相关《学年苏科版八年级数学初二上册第一章全等三角形单元测试含答案.docx(23页珍藏版)》请在冰豆网上搜索。
学年苏科版八年级数学初二上册第一章全等三角形单元测试含答案
第一章全等三角形单元测试
一、单选题(共10题;共30分)
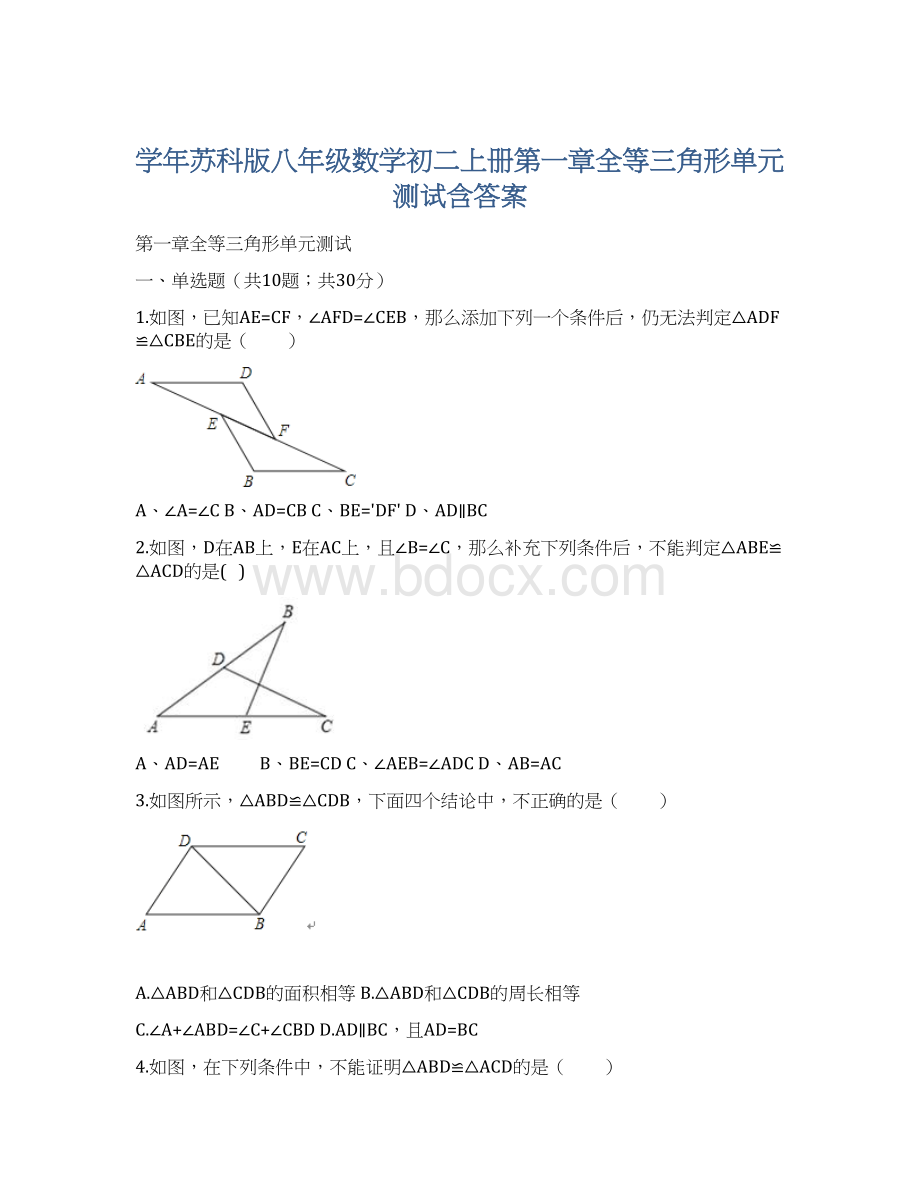
1.如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
A、∠A=∠CB、AD=CBC、BE='DF'D、AD∥BC
2.如图,D在AB上,E在AC上,且∠B=∠C,那么补充下列条件后,不能判定△ABE≌△ACD的是( )
A、AD=AE B、BE=CDC、∠AEB=∠ADCD、AB=AC
3.如图所示,△ABD≌△CDB,下面四个结论中,不正确的是( )
A.△ABD和△CDB的面积相等B.△ABD和△CDB的周长相等
C.∠A+∠ABD=∠C+∠CBDD.AD∥BC,且AD=BC
4.如图,在下列条件中,不能证明△ABD≌△ACD的是( )
A.BD=DC,AB=ACB.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CADD.∠B=∠C,BD=DC
5.已知图中的两个三角形全等,则∠1等于( )
A.72°B.60°C.50°D.58°
6.两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:
①△ABD≌△CBD;②AC⊥BD;③四边形ABCD的面积=12AC•BD,其中正确的结论有( )
A.0个B.1个C.2个D.3个
7.如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是( )
A.AB=ACB.∠BAE=∠CADC.BE=DCD.AD=DE
8.如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
A.∠M=∠NB.AM=CNC.AB=CDD.AM∥CN
9.已知△ABC≌△DEF,∠A=50°,∠B=75°,则∠F的大小为( )
A.50°B.55°C.65°D.75°
10.如图,在△ABC和△DEF中,给出以下六个条件中,以其中三个作为已知条件,不能判断△ABC和△DEF全等的是( )①AB=DE;②BC=EF;③AC=DF;④∠A=∠D;⑤∠B=∠E;⑥∠C=∠F.
A、①⑤②B、①②③C、④⑥①D、②③④
二、填空题(共8题;共27分)
11.如图,△ABC≌△ADE,∠B=100°,∠BAC=30°,那么∠AED=________°.
12.如图所示,已知△ABC≌△ADE,∠C=∠E,AB=AD,则另外两组对应边为________,另外两组对应角为________.
13.如图,△ACE≌△DBF,点A、B、C、D共线,若AC=5,BC=2,则CD的长度等于________.
14.如图,AB=AD,只需添加一个条件________,就可以判定△ABC≌△ADE.
15.△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为________.
16.如图,已知△ABC≌△DCB,∠BDC=35°,∠DBC=50°,则∠ABD=________.
17.如图,△ABC≌△DEF,点F在BC边上,AB与EF相交于点P.若∠DEF=40°,PB=PF,则∠APF=________°.
18.如图,在△ABC与△ADC中,已知AD=AB,在不添加任何辅助线的前提下,要使△ABC≌△ADC,只需再添加的一个条件可以是________.
三、解答题(共5题;共37分)
19.如图,已知△ABC≌△BAD,AC与BD相交于点O,求证:
OC=OD.
20.图中所示的是两个全等的五边形,∠β=115°,d=5,指出它们的对应顶点•对应边与对应角,并说出图中标的a,b,c,e,α各字母所表示的值.
21.如图,AB=CB,BE=BF,∠1=∠2,证明:
△ABE≌△CBF.
22.已知命题:
如图,点A,D,B,E在同一条直线上,且AD=BE,∠A=∠FDE,则△ABC≌△DEF.判断这个命题是真命题还是假命题,如果是真命题,请给出证明;如果是假命题,请添加一个适当条件使它成为真命题,并加以证明.
23.如图,已知点C是线段AB上一点,直线AM⊥AB,射线CN⊥AB,AC=3,CB=2.分别在直线AM上取一点D,在射线CN上取一点E,使得△ABD与△BDE全等,求CE2的值.
四、综合题(共1题;共10分)
24.定义:
我们把三角形被一边中线分成的两个三角形叫做“朋友三角形”.
性质:
“朋友三角形”的面积相等.
如图1,在△ABC中,CD是AB边上的中线.
那么△ACD和△BCD是“朋友三角形”,并且S△ACD=S△BCD.
应用:
如图2,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=AD=4,BC=6,点E在BC上,点F在AD上,BE=AF,AE与BF交于点O.
(1)求证:
△AOB和△AOF是“朋友三角形”;
(2)连接OD,若△AOF和△DOF是“朋友三角形”,求四边形CDOE的面积.
拓展:
如图3,在△ABC中,∠A=30°,AB=8,点D在线段AB上,连接CD,△ACD和△BCD是“朋友三角形”,将△ACD沿CD所在直线翻折,得到△A′CD,若△A′CD与△ABC重合部分的面积等于△ABC面积的
,则△ABC的面积是________(请直接写出答案).
答案解析
一、单选题
1、【答案】B
【考点】全等三角形的判定
【解析】【分析】由AE=CF可得AF=CE,再有∠AFD=∠CEB,根据全等三角形的判定方法依次分析各选项即可.
【解答】∵AE=CF
∴AE+EF=CF+EF,即AF=CE,
∵∠A=∠C,AF=CE,∠AFD=∠CEB,∴△ADF≌△CBE(ASA)
∵BE=DF,∠AFD=∠CEB,AF=CE,∴△ADF≌△CBE(SAS)
∵AD∥BC,∴∠A=∠C,∵∠A=∠C,AF=CE,∠AFD=∠CEB,∴△ADF≌△CBE(ASA)
故A、C、D均可以判定△ADF≌△CBE,不符合题意
B、AF=CE,AD=CB,∠AFD=∠CEB无法判定△ADF≌△CBE,本选项符合题意.
【点评】全等三角形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.
2、【答案】C
【考点】全等三角形的判定
【解析】【分析】A、根据AAS(∠A=∠A,∠C=∠B,AD=AE)能推出△ABE≌△ACD,正确,故本选项错误;
B、根据AAS(∠A=∠A,∠B=∠C,BE=CD)能推出△ABE≌△ACD,正确,故本选项错误;
C、三角对应相等的两三角形不一定全等,错误,故本选项正确;
D、根据ASA(∠A=∠A,AB=AC,∠B=∠C)能推出△ABE≌△ACD,正确,故本选项错误;
故选C.
3、【答案】C
【考点】全等三角形的性质
【解析】【解答】解:
A、∵△ABD≌△CDB,
∴△ABD和△CDB的面积相等,故本选项错误;
B、∵△ABD≌△CDB,
∴△ABD和△CDB的周长相等,故本选项错误;
C、∵△ABD≌△CDB,
∴∠A=∠C,∠ABD=∠CDB,
∴∠A+∠ABD=∠C+∠CDB≠∠C+∠CBD,故本选项正确;
D、∵△ABD≌△CDB,
∴AD=BC,∠ADB=∠CBD,
∴AD∥BC,故本选项错误;
故选C.
【分析】根据全等三角形的性质得出对应角相等,对应边相等,推出两三角形面积相等,周长相等,再逐个判断即可.
4、【答案】D
【考点】全等三角形的判定
【解析】【解答】解:
A、∵在△ABD和△ACD中
∴△ABD≌△ACD(SSS),故本选项错误;
B、∵在△ABD和△ACD中
∴△ABD≌△ACD(SAS),故本选项错误;
C、∵在△ABD和△ACD中
∴△ABD≌△ACD(AAS),故本选项错误;
D、不符合全等三角形的判定定理,不能推出△ABD≌△ACD,故本选项正确;
故选D.
【分析】全等三角形的判定定理有SAS,ASA,AAS,SSS,根据全等三角形的判定定理逐个判断即可.
5、【答案】D
【考点】全等三角形的性质
【解析】【解答】解:
如图,由三角形内角和定理得到:
∠2=180°﹣50°﹣72°=58°.
∵图中的两个三角形全等,
∴∠1=∠2=58°.
故选:
D.
【分析】根据三角形内角和定理求得∠2=58°;然后由全等三角形是性质得到∠1=∠2=58°.
6、【答案】D
【考点】全等三角形的判定
【解析】【解答】解:
在△ABD与△CBD中,
AD=CDAB=BCDB=DB,
∴△ABD≌△CBD(SSS),
故①正确;
∴∠ADB=∠CDB,
在△AOD与△COD中,
,
∴△AOD≌△COD(SAS),
∴∠AOD=∠COD=90°,AO=OC,
∴AC⊥DB,
故②正确;
四边形ABCD的面积=S△ADB+S△BDC=12DB×OA+12DB×OC=12AC·BD
故③正确;
故选D.
【分析】先证明△ABD与△CBD全等,再证明△AOD与△COD全等即可判断.
7、【答案】D
【考点】全等三角形的性质
【解析】【解答】解:
∵△ABE≌△ACD,∠1=∠2,∠B=∠C,∴AB=AC,∠BAE=∠CAD,BE=DC,AD=AE,
故A、B、C正确;
AD的对应边是AE而非DE,所以D错误.
故选D.
【分析】根据全等三角形的性质,全等三角形的对应边相等,全等三角形的对应角相等,即可进行判断.
8、【答案】B
【考点】全等三角形的判定
【解析】【解答】解:
A、∠M=∠N,符合ASA,能判定△ABM≌△CDN,故A选项不符合题意;B、根据条件AM=CN,MB=ND,∠MBA=∠NDC,不能判定△ABM≌△CDN,故B选项符合题意;
C、AB=CD,符合SAS,能判定△ABM≌△CDN,故C选项不符合题意;
D、AM∥CN,得出∠MAB=∠NCD,符合AAS,能判定△ABM≌△CDN,故D选项不符合题意.
故选:
B.
【分析】根据普通三角形全等的判定定理,有AAS、SSS、ASA、SAS四种.逐条验证.
9、【答案】B
【考点】全等三角形的性质
【解析】【解答】解:
∵∠A=50°,∠B=75°,又∵∠A+∠B+C=180°,
∴∠C=55°,
∵△ABC≌△DEF,
∴∠F=∠C,
即:
∠F=55°.
故选B.
【分析】由∠A=50°,∠B=75°,根据三角形的内角和定理求出∠C的度数,根据已知△ABC≌△DEF,利用全等三角形的性质得到∠F=∠C,即可得到答案.
10、【答案】D
【考点】全等三角形的判定
【解析】【解答】解:
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS);
∴A不符合题意;
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS);
∴B不符合题意;
在△ABC和△DEF中,
,
∴△ABC≌△DEF(AAS),
∴C不符合题意;
在△ABC和△DEF中,
D②③④不能判断△ABC和△DEF全等,
故选D.
【分析】根据全等三角形的判定方法对组合进行判断即可.
二、填空题
11、【答
- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 学年 苏科版 八年 级数 初二 上册 第一章 全等 三角形 单元测试 答案
 冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。


 (完整word版)信息论与编码期末考试题----学生复习用.doc
(完整word版)信息论与编码期末考试题----学生复习用.doc
 (完整版)固定资产盘点表.xls
(完整版)固定资产盘点表.xls
