正弦扫频信号幅值及相位的提取.docx

正弦扫频信号幅值及相位的提取.docx

《正弦扫频信号幅值及相位的提取.docx》由会员分享，可在线阅读，更多相关《正弦扫频信号幅值及相位的提取.docx（11页珍藏版）》请在冰豆网上搜索。

正弦扫频信号幅值及相位的提取

正弦扫频信号幅值及相位的提取

（1）

正弦振动控制系统提供输入的扫频信号

，对于对数扫频，

，其中Sr为对数扫描率，若频响函数为

则系统输出为

。

   测量系统中可得到Calo信号及响应信号，通过对二者进行数据处理，可得到频域下的响应

。

不知道LMS的信号采集软件是如何提取频域响应的，个人认为软件计算速度有限，LMS应该是通过硬件实现的。

下面我提供几种方法并进行比较。

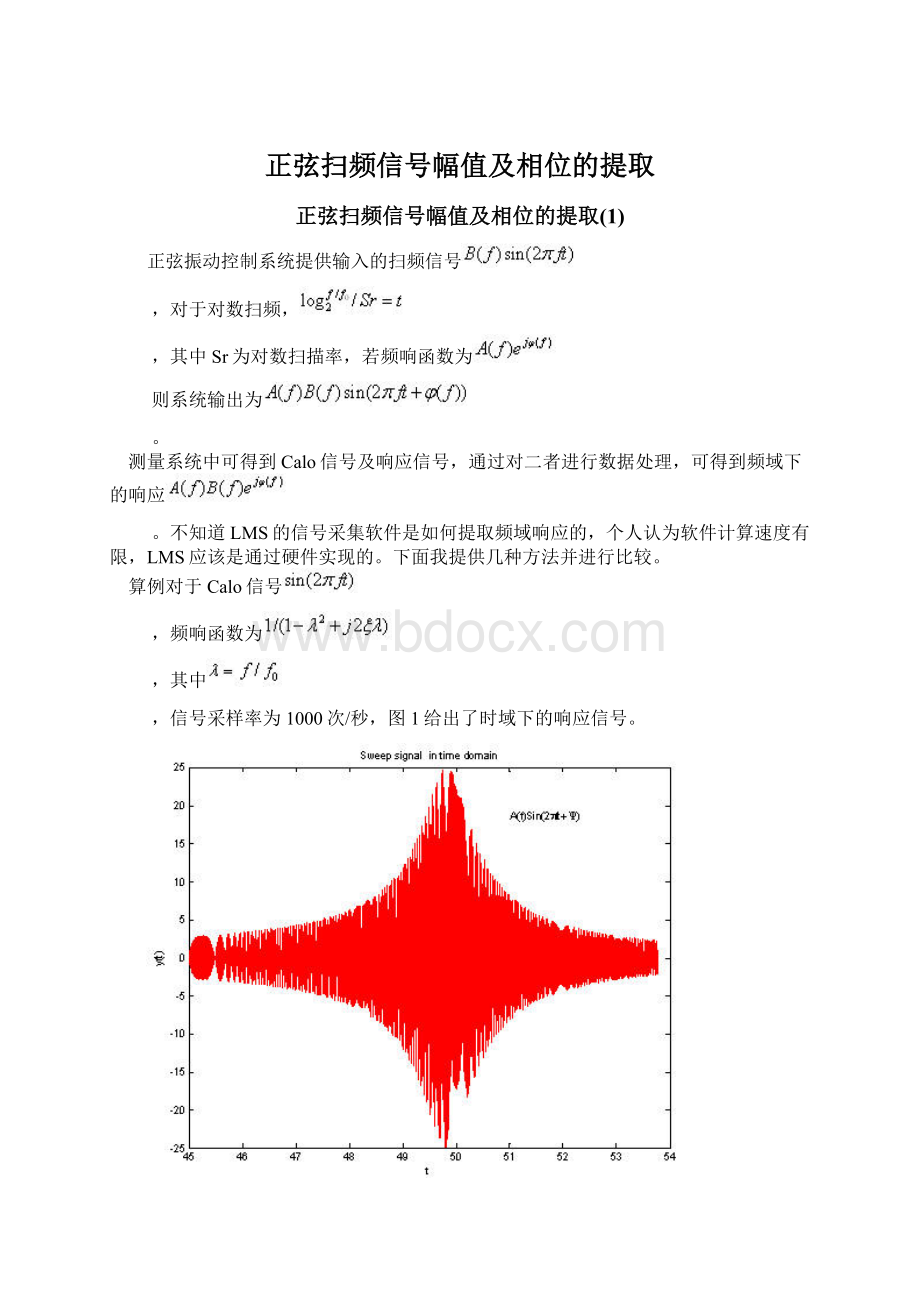
   算例对于Calo信号

，频响函数为

，其中

，信号采样率为1000次/秒，图1给出了时域下的响应信号。

图1 时域下的响应信号

正弦扫频信号幅值及相位的提取

（2）

方法1 分段FFT

   在[f,f+df]区间内对Calo信号、响应信号进行FFT变换，二者在频率f处的谱值比即为频响函数在f处的值。

此方法的缺陷是由于信号采样率为1000Hz，而[f,f+df]的区间很窄，在此区间下时域的点不会很多，因而FFT的频率分辨率不高。

  对于没有相位差的扫频信号，此方法能较好的提取幅值。

图2给出了使用此方法提取的幅值与理论结果比较，由图中可以看出二者基本吻合。

图2 使用分段FFT提取的频域幅值

   对于有相位差的扫频信号，则要对结果进行光滑处理，Matlab的smooth函数提供了这一功能。

图3给出了有相位差时分段FFT提取的幅值与相位同理论结果的比较，从图中可以看出在频域峰值处分段FFT比理论值大，在其余频段二者吻合较好。

图3 使用分段FFT提取的频域幅值、相位   

   下面给出了实现分段FFT提取扫频信号的频域幅值、相位的Matlab代码。

----------------------------------------------------------------------

%Decomposetheamplitudeandphasefromthesweepsignal

%Localfftandsmoothareemployed.

f1=5; %theinitialfreq

s=4;  %sweeprate

fr=50;%Resonantfreq

af=[];%amplitude

pf=[];%phase

k1=0.02;%dampingratio

df=0.01;%freqinterval

forfa=40:

df:

60

   t1=60/s*log2（fa/f1）;

   t2=60/s*log2（（fa+df）/f1）;

   ta=t1:

0.001:

t2;

   N=length（ta）;

   ft=f1*2.^（s/60*ta）;

   A1=sin（2*pi*ft.*ta）;

   lamb=ft/fr;

   B1=1./（1-lamb.^2+j*2*k1*lamb）;%transferfunction

   A2=abs（B1）.*sin（2*pi*ft.*ta+angle（B1））;

   ffreq=exp（-j*2*pi*（fa-400）*ta）; %freqshiftfortimedomain

   spa=fft（ffreq.*A1）;

   spb=fft（ffreq.*A2）;

   spr=abs（spb./spa）;

   spp=angle（spb./spa）;

   k=ceil（N*0.001*400）;

   af=[af,spr（k+1）];

   pf=[pf,spp（k+1）];

end

af=smooth（af,7）;

pf=smooth（pf,7）; %Keytrick

fa=40:

df:

60;

lamb=fa/fr;

bf=abs（1./（1-lamb.^2+j*2*k1*lamb））;

subplot（2,1,1）;

plot（fa,af,'r-',fa,bf,'b-.'）;

legend（'NumericResult','TheoreticResult'）;

title（'AmplitudeofSweepSignal'）;

xlabel（'f'）;

ylabel（'A（f）'）;

subplot（2,1,2）;

bpf=angle（1./（1-lamb.^2+j*2*k1*lamb））;

plot（fa,180/pi*pf,'r-',fa,180/pi*bpf,'b-.'）;

legend（'NumericResult','TheoreticResult'）;

title（'PhaseofSweepSignal'）;

xlabel（'f'）;

ylabel（'\Psi（f）'）;

-----------------------------------------------------------------------

   分段FFT提取方法计算速度一般，不会出现异常而中止，计算精度基本也能保证。

正弦扫频信号幅值及相位的提取（3）

方法2 分段曲线拟合

   在[f,f+df]区间内，假定A，ψ不变，此区间内在时域内对其拟合。

图4给出了有相位差时曲线拟合提取的幅值与相位同理论结果的比较，从图中可以看出计算结果与真实值吻合非常好。

图4 使用分段曲线拟合提取的频域幅值、相位

   分段曲线拟合提取的结果精度非常高，但是由于是拟合方法，因而可能会由于初始值给的不合理或拟合关系式不恰当而出现迭代次数超过规定值从而导致计算中止。

下面给出了实现分段曲线拟合提取扫频信号的频域幅值、相位的Matlab代码。

---------------------------------------------------------------

%Decomposetheamplitudeandphasefromthesweepsignal

%Localcurvefitisapplied.

f1=5; %theinitialfreq

s=4;  %sweeprate

fr=50;%Resonantfreq

af=[];%amplitude

k1=0.02;%dampingratio

df=0.01;%freqincrease

a=[]; %amplitude

ph=[];%phase

x0=[1,0];%initialguess

forfa=40:

df:

60;

   t1=60/s*log2（fa/f1）;

   t2=60/s*log2（（fa+df）/f1）;

   ta=t1:

0.001:

t2;

   N=length（ta）;

   ft=f1*2.^（s/60*ta）;  

   lamb=ft/fr;

   B1=1./（1-lamb.^2+j*2*k1*lamb）;%transferfunction

   A1=abs（B1）.*sin（2*pi*ft.*ta+angle（B1））;  

   xd=2*pi*ft.*ta;

   opt=optimset（'Display','off'）;

   x=lsqnonlin（'fsin',x0,[0,-pi],[inf,pi],opt,xd,A1）;

   x0=x; %Keytrick

   a=[a,x

（1）];

   ph=[ph,x

（2）];

end

ft=40:

df:

60;

lamb=ft/fr;

B1=1./（1-lamb.^2+j*2*k1*lamb）;%transferfunction

subplot（2,1,1）;

plot（ft,a,'r-',ft,abs（B1）,'b-.'）;

title（'MagnitudeofSweepSignal'）;

legend（'NumericResult','TheoreticResult'）;

xlabel（'f'）;

ylabel（'A（f）'）;

subplot（2,1,2）;

plot（ft,180/pi*ph,'r-',ft,180/pi*angle（B1）,'b-.'）;

title（'PhaseofSweepSignal'）;

legend（'NumericResult','TheoreticResult'）;

xlabel（'f'）;

ylabel（'\Psi（f）'）;

------------------------------------------------------------------

functiony=fsin（x,ot,yd）

a=x

（1）; %amplitude  otisomega*t

ph=x

（2）;%phaseinradian

y=a*sin（ot+ph）-yd;

-------------------------------------------------------------------

   由于相隔此次的频率相距很近，因而把上一次拟合的结果作为本次的初值，不但可以保证初始值给得非常合理，同时可以加快计算速度。

另外要强调的是尽管如此，由于每个频率段都要使用拟合，因而分段曲线拟合方法计算速度比较慢。

正弦扫频信号幅值及相位的提取（4）

方法3 分段两点求解

   在[f,f+df]区间内，利用两点求出两个未知数A，ψ，在[f,f+df]区间内对A，ψ取平均。

图5给出了有相位差时曲线拟合提取的幅值与相位同理论结果的比较，从图中可以看出计算结果与真实值基本重合。

由于算例中的扫频信号是理想的正弦扫频信号，因而两点求解能够精确计算得到真实值。

图5 使用分段两点求解提取的频域幅值、相位

   下面给出了实现分段两点求解提取扫频信号的频域幅值、相位的Matlab代码。

---------------------------------------------------------------------

%Decomposetheamplitudeandphasefromthesweepsignal

%Gettingtwoparametersthroughtwopoints

f1=5; %theinitialfreq

s=4;  %sweeprate

fr=50;%Resonantfreq

af=[];%amplitude

phf=[];%phase

k1=0.02;%dampingratio

df=0.01;%freqincrease

forfa=40:

df:

60

   t1=60/s*log2（fa/f1）;

   t2=60/s*log2（（fa+df）/f1）;

   ta=t1:

0.001:

t2;

   N=length（ta）;

   ft=f1*2.^（s/60*ta）;

   A1=sin（2*pi*ft.*ta）;

   lamb=ft/fr;

   B1=1./（1-lamb.^2+j*2*k1*lamb）;%transferfunction

   A2=abs（B1）.*sin（2*pi*ft.*ta+angle（B1））;

   amp=0;

   ph=0;

   fornk=2:

N

       T1=[sin（2*pi*ft（nk-1）*ta（nk-1））,cos（2*pi*ft（nk-1）*ta（nk-1））;...

           sin（2*pi*ft（nk）*ta（nk））,cos（2*pi*ft（nk）*ta（nk））];

       b1=[A2（nk-1）;A2（nk）];

       X=T1\b1;

       amp=amp+sqrt（sum（X.^2））;

       ph=ph+angle（X

（1）+j*X

（2））;

   end

   af=[af,amp/（N-1）];

   phf=[phf,ph/（N-1）];

end

fa=40:

df:

60;

lamb=fa/fr;

bf=abs（1./（1-lamb.^2+j*2*k1*lamb））;

subplot（2,1,1）;

plot（fa,af,'r-',fa,bf,'b-.'）;

legend（'NumericResult','TheoreticResult'）;

title（'MagnitudeoftheSweepSignal'）;

xlabel（'f'）;

ylabel（'A（f）'）;

subplot（2,1,2）;

plot（fa,180/pi*phf,'r-',fa,180/pi*angle（1./（1-lamb.^2+j*2*k1*lamb））,'b-.'）;

legend（'NumericResult','TheoreticResult'）;

title（'PhaseoftheSweepSignal'）;

xlabel（'f'）;

ylabel（'\Psi（f）'）;

--------------------------------------------------------------------

   尽管分段两点求解计算精度高，求解速度快，但是由于在计算两参数时使用了矩阵求逆（2×2的矩阵），因而可能会由于相邻两点的线性相关导致矩阵退化计算无法进行而中止。

正弦扫频信号幅值及相位的提取（5）

方法4 峰值包络

   提取时域扫频曲线的峰值与谷值，通过对Colo信号、响应信号进行分析得到相应的频率及相位信息。

图6给出了峰值包络提取的幅值与相位同理论结果的比较。

图中进行了光滑处理，从图中可以看出提取的幅值在各频率都低于精确值，由于振幅是随频率变化的，时域的峰值只是振幅与相位二者综合后形成的，即该处出现峰值相位并非为π/2，峰值只是幅值与相位的正弦之积，因而实际幅值比峰值大。

由于相位是间接提取的，相比于幅值误差更大。

图6 使用峰值包络提取的频域幅值、相位

  下面给出了利用峰值包络提取扫频信号的频域幅值、相位的Matlab代码。

这里可能会出现当精确值为-180由于误差导致小于-180，由于相位一般定义为[-180,180]，因而此时相位接近180，尽管只是表示形式的差别，但显示在相位曲线上就谬以千里了，故这里进行了特殊处理，即将相位表示为精确值与误差值之和，由于相位的误差值在很小的范围内，因而就避免了上述相位表示的问题。

图中当相位低于-180时，即以小于-180的形式表示。

--------------------------------------------------------------------

%Decomposetheamplitudeandphasefromthesweepsignal

%Searchingpeaksfromtimedomaincurve

f1=5; %theinitialfreq

s=4;  %sweeprate

fr=50;%Resonantfreq

af=[];%amplitude

pf=[];%phase

k1=0.02;%dampingratio

df=20; %freqincrease

nk=[];%thenumberofpeakpointsinthecurve

fa=40;

t1=60/s*log2（fa/f1）;

t2=60/s*log2（（fa+df）/f1）;

ta=t1:

0.001:

t2;

N=length（ta）;

ft=f1*2.^（s/60*ta）;

A1=sin（2*pi*ft.*ta）;

lamb=ft/fr;

B1=1./（1-lamb.^2+j*2*k1*lamb）;%transferfunction

A2=abs（B1）.*sin（2*pi*ft.*ta+angle（B1））;

fori=2:

N-1

   ifA2（i）>A2（i-1）&&A2（i）>A2（i+1）%peak

       nk=[nk,i];

       pa=angle（sin（2*pi*ft（i）*ta（i））+j*cos（2*pi*ft（i）*ta（i）））;

       pf=[pf,pa];

   elseifA2（i）

       nk=[nk,i];

       pa=angle（-sin（2*pi*ft（i）*ta（i））-j*cos（2*pi*ft（i）*ta（i）））;

       pf=[pf,pa];

   end

end

tb=ta（nk）;

fa=f1*2.^（s/60*tb）; %thecorrespondingfreqforthepeak

af=abs（A2（nk））;

frb=fa/fr;

pf2=angle（1./（1-frb.^2+j*2*k1*frb））;

pf=pf2+angle（cos（pf-pf2）+j*sin（pf-pf2））;%Keytrick

af=smooth（af,7）;

pf=smooth（pf,7）;

fb=40:

0.01:

60;

lamb=fb/fr;

bf=abs（1./（1-lamb.^2+j*2*k1*lamb））;

bpf=angle（1./（1-lamb.^2+j*2*k1*lamb））;

subplot（2,1,1）;

plot（fa,af,'r-',fb,bf,'b-.'）;

legend（'NumericResult','ExtractResult'）;

title（'MagnitudeoftheSweepSignal'）;

xlabel（'f'）;

ylabel（'A（f）'）;

subplot（2,1,2）;

plot（fa,180/pi*pf,'r-',fb,180/pi*bpf,'b-.'）;

legend（'NumericResult','ExtractResult'）;

title（'PhaseAngleoftheSweepSignal'）;

xlabel（'f'）;

ylabel（'\Psi（f）'）;

---------------------------------------------------------------------

   峰值包络提取仅包含简单的代数计算，不涉及复杂的运算，因而计算速度很快，而且也不会因异常中止。

当然天下没有免费的午餐，粗糙的加工也不会得到精致的结果，正如图6所示，峰值包络的计算结果精度很差。

而且它只能得到在峰、谷处频率的幅值与相位，对于对数扫频在高频处的频率点数就寥若晨星了。

   上面是使用标准的正弦对数扫频曲线，以及单自由度振动阻尼系统的响应为例，实际情况比这复杂得多，但原理基本相同。

下面从不同角度把上面几种方法的优缺点总结如下。

表1 几种方法的评价