井斜及其控制.docx

井斜及其控制.docx

《井斜及其控制.docx》由会员分享，可在线阅读，更多相关《井斜及其控制.docx（32页珍藏版）》请在冰豆网上搜索。

井斜及其控制

第六章井斜及其控制

在钻井工作中不但要求速度快，而且要求质量好。

井身质量的好坏是油气井完井质量的前提和基础，它直接关系到油、气田的勘探和开发工作。

如果井眼斜度（井斜）过大，会使井眼偏离设计井位，将打乱油气田开发的布井方案。

对于勘探工作来说，井斜大了，会使井深发生误差，使所得的地质资料不真实。

并由于井底远离设计井位，会错过油气层，造成勘探工作的失误，这对于断块小油田显得格外重要。

井打斜了，给钻井工作本身也增加不少困难，甚至造成严重事故。

在斜井内，钻柱易靠在井壁的一侧，旋转时发生严重摩擦，在井斜突变井段钻柱发生弯曲，易使钻柱磨损和折断，也可能造成井壁坍塌及键槽卡钻等事故。

一旦我们疏忽大意，井斜过大而超过要求时，就被迫中途填井纠斜，将造成很大浪费，并会推迟完井时间。

井斜大了，会直接影响固井质量。

首先是造成下套管困难，同时套管下入后不易居中，这往往是造成固井窜槽、管外冒油冒气的原因之一。

对采油工作来说，井斜过大会直接影响井下的分层开采、注水工作的正常进行（如下封隔器困难，封隔器密封不好等），对抽油井也常引起油管和抽油杆的磨损和折断，甚至造成严重的井下事故。

所以，井斜过大对油气田的勘探和开发都有很大危害。

如何控制井斜是钻井工作的一个重要课题。

我们要控制井斜，首先必须知道井斜是由哪些因素决定的（详见第七章定向钻井所述）。

一般说来，井斜可由井斜角，方位角，井底位移，井斜变化率等因素来衡量。

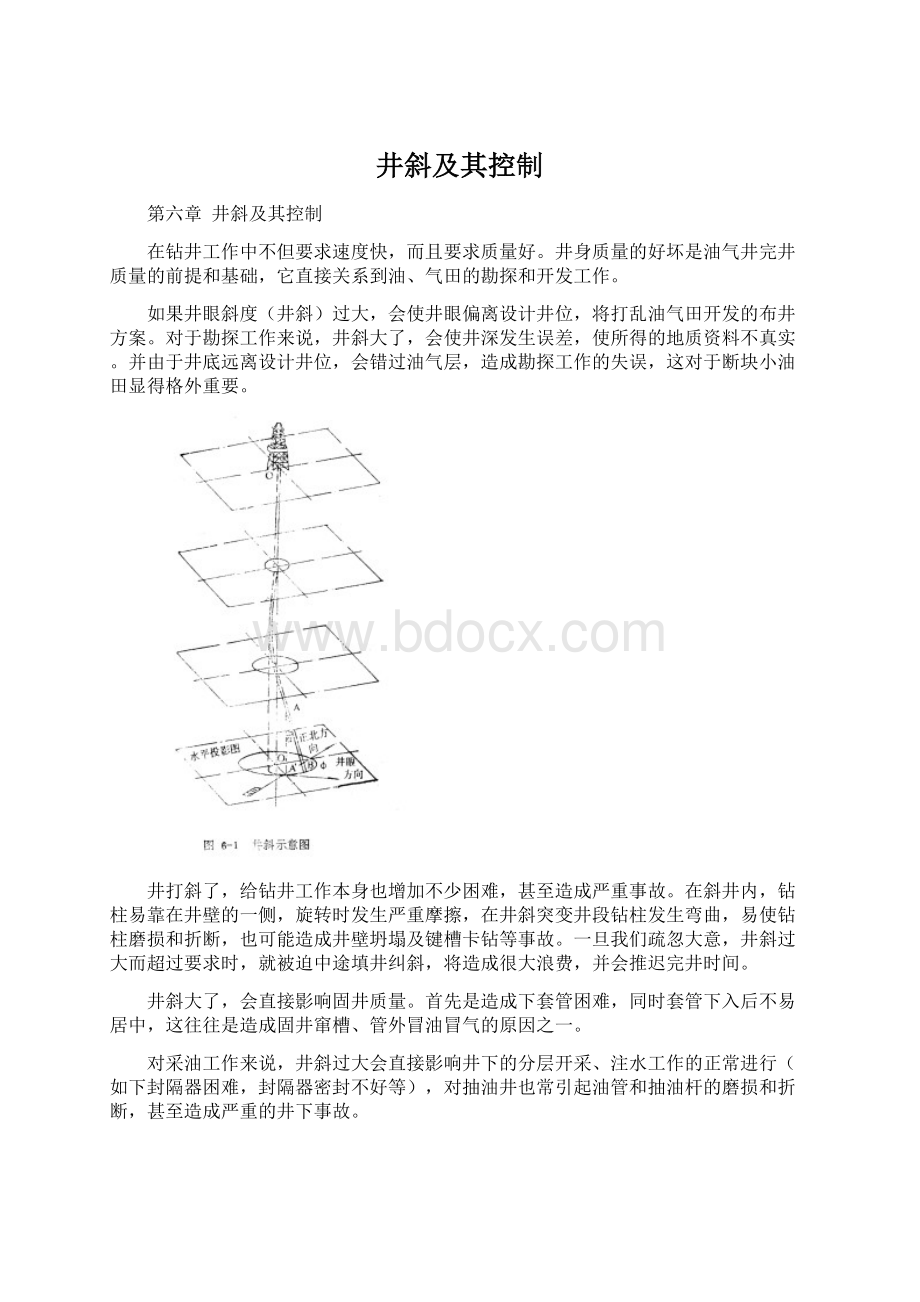
所谓井斜，即是一口井偏离了铅直线，如图6-1所示。

（1）井斜角（Ho1edeviationang1e）井斜角是指井眼轴线的切线与铅直线之间的夹角，一般以“α”表示（图6-1`中的α角为A点的井斜角）。

（2）方位角（Directiona1ang1eofdef1ection）方位角是表示井眼偏斜的方向，它是指井眼轴线的切线在水平面投影的方向与正北方向之间的夹角，一般以“φ”表示。

方位角是以正北方向开始，按顺时针方向计算的（图6-1中的φ角为A点的方位角）。

一般清况下，井眼铀线每一点的井斜角和方位角都在不断地变化，一口井的井眼轴线都是一条不规则的扭曲的空间曲线。

井眼轴线上任一点的井斜角和方位角都可通过电测得到。

因此我们可以根据一口井各个测点资料，从井口到井底把井眼轴线绘制出来（具体方法详见第七章定向钻井）。

（3）井底水平位移（Horizontaldeparture）井底水平位移麦示井底在水平面上偏离原井口的大小，它是指完钻井底与井口在水平面上投影之间的直线距离（图6-1中的O’B距离）。

一般来说，对于浅井或中深井，为了控制井斜，常给定一个全井的最大井斜角（如3度或5度）和全井最大水平位移（如30米或50米）来作为井身质量的标准。

但对深井或超深井来说，上述井斜标准就显得不那么合理了。

钻井实践说明，上述井斜标准主要意义在于使完井后井底位移不致过大，以满足地质开发上的最低要求。

事实上，常常引起事故或复杂情况的原因是井斜变化过大，而不是由于井斜本身大小所致。

因此在深井钻进时，应使井斜的变化尽量缓慢，钻出的井眼应无井斜角或方位角的突然变化（这种变化现场称为“狗腿”）。

因此，必须用一个井斜变化率指标来衡量井斜变化的大小，以便控制井斜。

（4）井斜变化率（Rateofdeviationchange）它是指单位长度（一般取30米或100米）内井斜角的变化值，而单位长度内方位角变化值则称为方位变化率。

上面谈到井斜是影响井身质量的重要因素，因此为了快速优质安全地完成钻井任务，确保井身质量，必须对控制井斜提出适当的要求，即井斜标准。

由于控制井斜在技术上是一项异常复杂的问题，故制定井斜标准也是一件困难的工作，需要通过实践不断总结、改进和完善。

国外主要以限制井眼曲率作为井斜标准。

美国学者Lubinskil961年发表论文[1]提出，最大允许的井眼曲率应以下述三个数值中最小的一个数值为准：

（1）钻杆不发生疲劳损坏；

（2）钻铤丝扣处不发生疲劳损坏；（3）钻杆与井壁之间的作用力不应大于8896.6牛（2000磅）。

经过数学推导，分别给出了三种情况下确定最大允许井眼曲率的计算公式，制作了便于查用的图表。

国外有的提出最大井眼曲率一般定为1.5～3°／30米。

现在对此标准又有放宽的趋势。

我国对井斜标准的规定，主要是限制井眼曲率为3°／100米。

至于对井斜角的规定，要根据各地区的具体情况而定。

目前是两个标准并提（即对井斜角有一定限制，而且又对井眼曲率有一定要求）。

以胜利油田为例，除井斜角、井眼曲率外，还提出了水平位移的限制。

详见表6-1。

四川石油管理局的井斜标准如下：

防斜和控制井斜技术的理论研究很早就为钻井学术界所重视，并列为重要的研究内容。

早在50年代，以美国学者Lubinski和Woods等人为代表[1]首先研究了光钻铤在钻压作用下的弯曲问题，探索了弯曲规律，导出了有关计算模式，在防斜问题的理论研究方面作了开创性的工作。

在此理论的基础上提出了在钻铤适当部位加一个稳定器来防斜（即钟摆钻具），并编制了一整套实用图表来计算稳定器的安置位置，为以后钟摆钻具防斜技术提供了理论依据。

60年代是以Hoch[14]为代表，根据钻柱在井内受到钻压的纵向作用，弯曲后因井壁的限制而受到井壁的反作用力，实际上是下部钻柱看成是纵横联合载荷的梁，以此为依据提出了双稳定器防斜钻具的理论，这是以后满眼钻具发展的基础之一，在Hoch理论指导下，60年代广泛使用了满眼钻具，以后又出现了在钻头上又加了一个近钻头稳定器，即至少有三个稳定器的钻具组合。

在“满眼”思想指导下，又出现了“方钻铤”、“螺旋钻铤”防斜，可以说满眼钻具的出现，使钻井的防斜问题取得了很大的进展。

1973年美国学者Walker[18]提出了用小势能法求解下部钻具的受力和变形，Amoco公司Millheim，和Warren[19]首先用有限元法求解钻柱下部结构的受力和变形，Shell公司的Fischer和Brad1y使用差分法求解下部钻柱的受力和变形。

以上三家研究的共同特点是，所提供的模式都能解出钻头上所受的侧向力和钻柱与井壁的切点上所受的力，计算程序都相当复杂，需要大型计算机，另外，由于力学模型过于简化，计算结果与实际都存有一定差距。

Lubinski在1983年曾来华讲学，系统介绍了70年代以来的研究成果，修正了过去研究中的不妥之处，并在过去研究的基础上，仍然用解微分方程的方法进一步求解多稳定器钻具组合的受力和变形，编制了计算机程序。

70年代以来，研究中的一个重要特点是把地层造斜的因素考虑进去，并用某个数学模式来表示。

Lubinski首先提出了“地层各向异性指数”的概念，石油工业出版社80年出版的《美国钻井手册》[20]中把地层的造斜能力分为21个等级（A、B、…T、U），并列表给出了不同地层倾角、不同井斜角、不同钻具组合和不同地层等级下应该使用的钻压值。

我国60年代以前基本是引用外国的理论和方法。

进入70年代逐步开展了对防斜理论的研究，首先是西南石油学院唐俊才等人[24]，深入研究了Hoch的防斜理论，指出了公式推导中的错误，并提出了修正公式。

70年代未，白家祉教授提出用纵横弯曲连续梁理论解下部钻柱的受力和变形[22]，并提出一种柔性钟摆钻具，这在防斜技术上开辟了一条新路子。

白教授在最近几年又分别用有限元法，最小势能法求解下部钻柱的受力和变形，并将求解结果与用纵横弯曲连续理论进行对比，得出了三个方法的结果基本上一致的结论。

四川钻采工艺研究所杨勋尧在最近几年，对钟摆钻具、满眼钻具都进行了研究[17、23]，得出了简化的公式和图表，并在川东现场上指导钻井实践，取得了较好的防斜效果。

另外，白、杨二人对地层造斜力也进行了一定的研究。

第一节井斜的原因

钻井实践表明，影响井斜的原因是多方面的，如地质条件，钻具结构，钻进技术措施，操作技术，以及设备安装质量等。

归纳起来，造成井斜的主要原因不外乎：

第一，从客观上来说，由于所钻地层的倾斜和非均质性使钻头受力不平衡而造成井斜；第二，从技术上来说，下部钻具的工作状态对井斜的影响很大，当下部钻具受压发生弯曲就会使钻头偏斜导致井斜；第三，从主观上来说就是操作是否合理。

即使有性能良好的防斜钻具，也会因操作不当而造成井斜。

一、地质条件[2][3]

地质条件是产生井斜的重要原因。

一般影响井斜的地质因素有：

地层倾角（Dipang1eofbedding）；层状结构；各向异性；岩性软、硬交替以及断层等。

但其中起主要作用的是地层倾角，其他诸因素对井斜的作用都与地层倾角紧密相连。

在有些地区观察到以下现象：

当地层倾角小于45°时，井眼一般沿上倾方向偏斜；当地层倾角大于60°时，井眼将顺着地层面下滑发生偏斜；而在45°至60°之间是不稳定区，即有时向上倾斜有时向下倾斜，这个不稳定区的范围是随各地区地层条件而不同。

以下我们分析在地层有倾角情况下影响井斜的地层因素。

（一）层状地层（Laminarformation）对井斜的影响[2]

有些地区井斜问题多发生在如页岩、砂岩等层状地层中，而较少发生在如石灰岩等均质地层中。

例如，渤海湾地区沙河街厚页岩及五七油田荆河镇中下部及潜一段等都是成层性很强的薄层页岩，很容易引起井斜。

如图6-2所示，当钻头在倾斜的层状地层中钻进时，当钻至每个层面交界处时，此处岩层不能长时间支持所加的钻压而趋向沿垂直层面发生破碎。

在井眼上倾一侧的小斜台很容易钻掉。

相反，在井眼下倾一侧却残留一个小斜台；它就象小变向器作用一样，对钻头施加一个横向力，把钻头推向上倾（Updip）的一侧，从而引起井斜。

这样，当钻头逐层钻进时，将使井斜不断增大，但最大也只能等于地层倾角。

当使用的钻压增大时，破碎将更加厉害，在每一层中形成更大的小斜台，从而引起更大的横向力，使井斜增长更快，所以，地层倾角越大，成层性越强，钻压越大，则井斜也就越大。

这种作用除造成井斜之外，而且会减少井眼的有效尺寸，可能引起以后其他事故的发生。

（二）地层各向异性（Anisotropyofformations）对井斜的影响[3]

从生产实践和实验室的研究得知，由于岩层的成层状况、层理、节理、纹理以及岩石的成分、结构、胶结物、颗粒大小等因素造成岩层在不同方向上的强度不同，一般来说垂直地层层面的强度较小，钻进时钻头将沿着这个破碎阻力最小的方向倾斜。

图6-3表示钻头在不同方向上的破碎速度（即可钻性）不同。

图6-3（a）中，1、2、3三个方向上的速度是Vt1＞Vt2＞Vt3。

由于地层水平，井眼不发生倾斜。

图6-3（b）中，地层倾斜，钻头趋向于垂直地层层面方向偏斜。

图6-3（C）中，地层呈垂直状态，由于垂直于层面的强度小，所以井壁岩石易破碎，钻头稳定性差，钻进时容易井斜，且方位不稳定。

鲁宾斯基[1]用岩石各向异性指数h来表示地层平行和垂直层面方向上岩石可钻性差异的程度，如设S1，S2分别表示平行和垂直层面方向上的岩石可钻性，则按照一般定义，岩石的各向异性指数h可写为：

式中，h’为平行和垂直层面方向岩石可钻性的比值。

各向异性指数h反映了地层两个方向上可钻性差异的程度。

如设h＝0.1，即意味着平行于层面方向的可钻性比垂直层面方向的可钻性低10%，这时h’等于0.9意即S1只为S2的90%。

鲁宾斯基使h值与地层造斜性联系并对应起来，地层造斜性分为由A到U共21级，每级相应的h值如表6-3所列。

为了适用于电子计算机，又提出一种由0到100的新的地层分级方法。

三种方法相对应的关系数据如表6-3所列[21]。

（三）岩性交替变化（岩性软硬交错）对井斜的影响

当钻头从软地层进入硬地层时，如图6-4（a）所示。

钻头在A侧接触到硬岩石，而在B侧还是软岩石。

这样在钻压作用下，由于A侧岩石的硬度大，可钻性小，钻头刀刃吃入地层少，钻速慢；而在B侧岩石的硬度小，可钻性大，钻头刀刃吃入地层多，钻速快，这样钻出井眼自然会偏斜。

另外，由于钻头两侧受力不均，在A侧的井底反力的合力比B侧大，将产生一个弯矩M，扭转钻头，使其沿着地层上倾方向发生倾斜。

当钻头由硬地层进入软地层时，如图6-4（b）所示，开始时由于地层在软地层一侧吃入多，钻速快，而在硬地层一侧吃入少，钻速慢，井眼有向地层下倾方向倾斜的趋势。

但当钻头快钻出硬地层时，此处岩石不能再支承钻头的重负荷，岩石将沿着垂直于层面方向发生破碎，在硬地层一侧留下一个台肩，迫使钻头回到地层上倾方向。

所以钻头由硬地层进入软地层也有可能仍然向地层上倾方向发生倾斜。

此外，断层（Fault）也常常会引起井斜。

这是由于多数断层在发生错动时，往往不是沿一个面，而是沿着一个破碎带。

很明显，由于破碎带的岩石疏松，当钻头进入破碎带时

形成受力不均，工作不稳定，也容易产生井斜。

总的来说，由于地质条件的影响，地层将作用于钻头一个横向造斜力，使钻头偏离原来的井眼轴线，一般情况下是使井眼向地层上倾方向发生偏斜。

另外，地层倾角越大，则其造斜力越强。

若单从地层因素来考虑，井斜角最大也不会超过地层倾角。

所以，地质条件仅是影响井斜的原因之一。

还需指出，通常地质上讲的地层倾角是就整个地质构造而言的。

而从实际观察岩心时发现，岩石层面的交角往往比地层倾角大得多（如图6-5所示）。

这和古地理的地面情况及沉积时的许多情况有关。

所以，有时地层倾角虽然很小，但由于层面交角大，也会引起井斜。

（四）地层造斜力的计算模式

国内外学者为了比较科学定量地描述地层因素对井斜的影响，曾试图用一地层造斜力Ff，来综合反映这一因素的大小。

根据地层各向异性理论，利用各向异性指数h的概念和井斜是钻头前进的轨迹偏离原来井眼轴线方向的基本定义，可以推导出地层造斜力Ff的计算式（详见附录）

式中，β1是地层倾角，α为井斜角，P为钻压，而K就是反映地层造斜能力大小的综合造斜系数，它取决于地层的各向异性指数h和地层相对于井底平面的倾斜角，即相对地层倾角（β1-α），K和h成正比；而K和相对地层倾角（β1-α）成正弦函数关系（图6-6）。

从图中可看出，当（β1-α）＝45°时K有极大值。

从式（6-1）可知，地层造斜力Ff和钻压成正比，当α=β1时，地层造斜力为0值；α>β1时，地层力实际为降斜力。

二、下部钻柱弯曲对井斜的影响[1]（Effectofdri1lstringbuckingonholedeviation）

在钻进时，是靠下放部分钻柱的重量给钻头形成钻压。

当钻压较小时，下部钻柱保持直线稳定状态，当钻压增至某一临界钻压时，则下部钻柱丧失稳定而发生弯曲（如图6-7所示）。

钻头及其相邻连接部分钻柱的中心线偏离井眼轴线，而使钻头偏离一个角度，称为钻头倾斜角β（Inc1inationoftheBit）。

钻头倾斜后，对井底形成了不对称切削，这是产生井斜重要因素。

显然，钻头倾斜角β越大，井斜也越大。

下部钻柱弯曲后，如图6-7所示，O点是钻柱的底端（即钻头），N1点是中性截面位置，ON1段是受压段，T1点是钻柱与井壁的接触点，称为捌点（Pointoftangency）。

钻柱弯曲形状和变化规律是根据模拟实验和理论分析得来的。

由于钻柱在井下的工作条件比较复杂，所以在进行理论分析和数学计算时，有必要作出以下假设[1]：

（1）下部钻柱内外都是等直径的光平管柱，钻柱两端为铰链约束；

（2）造成下部钻柱弯曲的原因主要是井下钻柱在泥浆中的自重使下部钻柱受轴向压力所造成，而不考虑井壁及泥浆对钻柱的摩擦力以及泥浆循环时钻柱内外压差等因素对钻柱弯曲的影响；

（3）不考虑钻井时扭矩对钻柱的影响，钻柱呈平面弯曲状态，同时假设钻柱是柔性体，绕自身轴线自转，离心力的合力为零。

图6-8为计算示意图。

作用在钻柱上的外力有：

吊卡对钻柱的向上拉力w1；井底反力的垂直分力w2，称为“钻压”；井底反力的水平分力F2；转盘方卡瓦的水平分力F1；当钻柱弯曲时井壁对钻柱的反力F。

此外还有图中未绘出的另两个力，一个是钻柱的重量，是垂直向下的力，另一个是泥浆对钻柱的浮力，是垂直向上的力。

此计算示意图的主要特点是考虑了井底的水平反力，并认为两端全是铰链；而在一般弹性理论问题中，仅考虑垂直反力，且上端为自由竖立的长杆。

虽然问题比较复杂，但比较接近钻柱的实际情况。

根据上述条件推出的弯曲钻柱微分方程为：

此方程式的求解比较复杂，可以通过运用幂级数和贝塞尔函数来求出方程式的近似解，或者用电子计算机求解。

最后可以得出钻柱弯曲的临界钻压值，切点位置，钻头倾角及弯矩等。

当下部钻柱发生弯曲时，中性截面N1距0点的距离L（见图6-7），近似等于受压部分长度ON1为

从上式中可以看出，钻柱发生弯曲的受压部分长度是钻柱刚度和在泥浆中单位长度函数，即取决于EJZ和qm的数值。

而这些数值是和钻柱的材料、截面形状、尺寸以及井内泥浆比重等有关。

为一便于计算，使所得结果和钻杆、钻铤及泥浆等的类型有关，我们用微分方程中定义的无因次单位m来表示钻柱的长度。

根据量纲分析，m的量纲应该是长度的一次幂。

一般我们把m称做一个无因次单位的长度。

这样，发生弯曲时钻柱受压部分长度即可方便地用下式表示：

发生弯曲时的临界钻压P为

常用钻铤、钻杆的临界钻压值列于表6-4中。

钻柱弯曲时的钻头倾斜角β为

从以上分析中可看出，钻柱弯曲对井斜的影响有以下两点：

（1）当钻压小于发生弯曲的临界钻压时，钻柱是直的，钻头无倾斜现象。

当钻压达到弯曲的临界钻压时，钻柱发生弯曲，产生钻头倾斜角。

如果钻压继续增大，则切点随之下降，钻头倾斜角也随之加大。

（2）当钻头直径一定时，井径越大，钻铤越细，则钻铤与井眼的间隙越大（即r越大），因而钻头倾斜角越大，井越容易钻斜。

所以为了防斜应使钻头倾斜角尽量小，宜选用直径大、刚性大的钻铤，并尽可能减小下部钻柱与井眼的间隙。

三、斜井内钻柱的受力分析[5][6]

以上我们分析了产生井斜的主观因素（下部钻柱弯曲等技术条件）和客观条件（地质因素），这只是研究了直井内的情况。

但是在斜井内（这是一般情况）井眼的斜度是增大还是减小或是保持某个平衡角度，就取决于钻头的受力情况。

我们在研究钻头受力情况时作以下假定[9]：

（1）钻头可象球窝节一样自由转动，但其横向运动受到约束。

（2）钻铤稳定地靠在井壁的低边。

（3）钻头由于受力情况不同，可自由地向任一方向切割。

图6-9为一斜井，井斜角为α，钻铤靠在井壁低边，并在切点T处与井壁接触。

显然，作用在钻头的力有

（一）钻压（Bitweight）

由于钻铤弯曲，钻压不是沿井眼轴线方向施加给钻头，而是偏离一个角度β．此时钻压可分解为与井眼轴线相平行的力P0和与井眼轴线相垂直的力Fj

它对井斜没有什么影响，而是使井眼沿着原井眼轴线的方向继续向下钻进。

Fj将使钻头偏离井眼轴线，造成井斜，为一增斜力。

（二）钟摆力（Pendulumforce）

井眼偏斜后，在斜井内钻柱切点以下的重量W势必在垂直于井壁方向产生一个分力，此力与钟摆作用相似，将趋使钻头破碎井眼低侧岩石，使井眼恢复垂直状态，所以为一减斜力。

作用在钻头上的减斜力Fd近似等于[10]

（三）地层造斜力Ff（Deflectingforceoftheformation）

它取决于地层倾角和各向异性等因素。

在多数情况下增斜，也可能为降斜（当钻水平地层时）。

综合考虑上述诸力的作用，在钻头上作用一对相互矛盾着的力，即：

造斜力

（6-10）

自然增斜时Ff取正号，自然降斜时取负号。

降斜力

在这两种力的作用下，当造斜力F1等于降斜力Fd时形成平衡状态，则保持已有井斜角α。

当造斜力F1大于降斜力Fd时，井斜角将增大。

与此同时降斜力也相应加大（因α角增大），所以将达到一个大于α的新的平衡角。

当降斜力Fd大于造斜力F1时，井斜角将减小，而达到一个小于α的新的平衡角。

在各向同性的地层中，井斜平衡角数值主要取决于三个因素：

即钻压，钻铤尺寸和井眼尺寸[6]。

1．钻压

加大钻压将加大钻头以上钻铤未受支撑部分的弯曲，使切点移向钻头。

其结果是钻头倾斜角加大，增斜力Fj增大，同时切点以下钻铤重量W减小，钟摆力也减小。

因而，增大钻压会明显引起井斜的加大。

2．钻铤尺寸和井眼尺寸（Sizeoftheho1eandCollars）

这两个因素是通过它们之间的间隙值（C1earance）而互相关联着。

现在考虑间隙为常数时，钻铤尺寸的影响。

当钻压相同时，由于大钻铤的刚度大，不易弯曲，切点位置较高，因而钻头倾斜角小，可在一定程度上减小增斜力Fj。

更主要的是切点以下钻铤长度大些，加之大钻铤单位长度重量大，使钟摆力加大，从而可减小平衡角。

另外，使用大尺寸钻铤，在保证同样井斜平衡角的条件下，可允许增加钻压，提高钻速。

在各向异性地层中，平衡角还取决于地层特性[1]。

一般来说，地层特性可通过地层倾角和地层各向异性指数来表示。

在各向异性地层中，由于垂直层面可钻性一般大于平行层面可钻性，因而钻头趋向于垂直地钻进地层，钻头常向上倾方向钻进。

所以，在各向异性地层中，井眼偏斜可能比各向同性地层大些。

第二节钟摆钻具控制井斜技术

钟摆法的实质是通过使用专用的防斜钻具组合及相应的技术措施来增大钟摆减斜力，以平衡和克服促使井斜的地层力。

属于这种方法的有：

钟摆钻具、偏重钻铤和塔式钻铤。

一、钟摆钻具的防斜原理及使用特点[1]

（一）工作原理

它是利用斜井内切点以下钻铤重量的横向分力把钻头推向井壁下方，以达到逐渐减小井斜的效果。

这个横向分力的作用犹如钟摆一样，所以称它为“钟摆力”，运用这个原理组合的钻具称为钟摆钻具。

图6-10为钟摆钻具（pendulumassemb1y）示意图。

切点T以下钻铤长度（又称悬臂段）为L，在泥浆中单位长度钻铤的重量为qm，井斜角为α，则

钟摆力＝Lqmsinα

作用在钻头上的减斜力LFd≈1/2Lqmsinα。

从上式可看出，对一定斜度的井眼来说，井斜角α是一定的，因此增大纠斜力的主要办法是增大切点以下钻铤的重量Lqm，其办法有二。

一个办法是使用大尺寸钻铤或加重钻铤（见图6-11）。

在同一钻压下，不易被压弯，且切点位置高，因而切点以下钻铤长度L大，有利于增大减斜力。

另一个办法是在此切点略高一些的位置上，安装一个稳定器，以提高切点位置，增大其下部钻铤的重量，使减斜作用增大（如图6-11所示）。

除此之外，稳定器对其下部钻铤还起到扶正作用，因而可减小钻头倾斜角，限制增斜力的作用。

当然，最理想的办法是大尺寸钻铤加稳定器，这样所组成的钟摆的长度大，重量也大，其减斜效果最好。

（二）稳定器安放位置（Positionofstabilizers）

对钟摆钻具来说，稳定器的安放位置十分重要，它是这种钻具的技术关键。

如果安放偏低则减斜力小，效果差；如果安放偏高，则稳定器以下钻铤可能与井壁形成新的切点，使钟摆钻具失效。

稳定器安放的理想位置（Idealpositionofstabilizer）可以认为是在保证稳定器以下钻铤不与井壁接触的条件下尽量提高些，如图6-12所示。

稳定器位置主要取决于钻铤尺寸，钻压大小和井眼斜度等。

[2]

当钻铤尺寸较大，在同一钻压下钻具发生弯曲后的切点位置比小尺寸钻铤要高一些，因此稳定器也应随之安放高一些，以增大钟摆减斜力。

钻压对稳定器的位置影响很大。

当钻压增大时（在同一弯曲状态时），切点下移，稳定器也应随之下移，否则会在稳定器以下形成切点，这就是常使钟摆钻具失效的原因之一。

反之，钻压减小时，切点上移，稳定器也应上提，以发挥钟摆钻具的作用。

井眼斜度也有影响，斜度大，在钻具自重作用下易与井壁接触，因而切点相对低些，稳定器位置也应随之下降些。

另外，随着稳定器与井眼间隙增大，稳定器位置也要相应下移。

这是因为在相同钻压下，间隙越大，稳定器的效果越差，若间隙过大时下部钻具也容易与井壁形成新的切点。

通过计算机计算和钻井