数学建模 实验报告.docx

数学建模 实验报告.docx

《数学建模 实验报告.docx》由会员分享，可在线阅读，更多相关《数学建模 实验报告.docx（12页珍藏版）》请在冰豆网上搜索。

数学建模实验报告

《数学建模》实验报告

实验序号：

实验8　　　　　　　　　实验项目名称：

统计回归模型

学　　号

1210012143

姓　　名

詹建妹

专业、班

12信计

实验地点

实4-401

指导教师

吴春红

实验时间

2014.4.29

一、实验目的及要求

通过对具体实例的分析，学会运用统计回归方法建立模型的方法。

二、实验设备（环境）及要求

多媒体机房，单人单机，独立完成

三、实验容与步骤

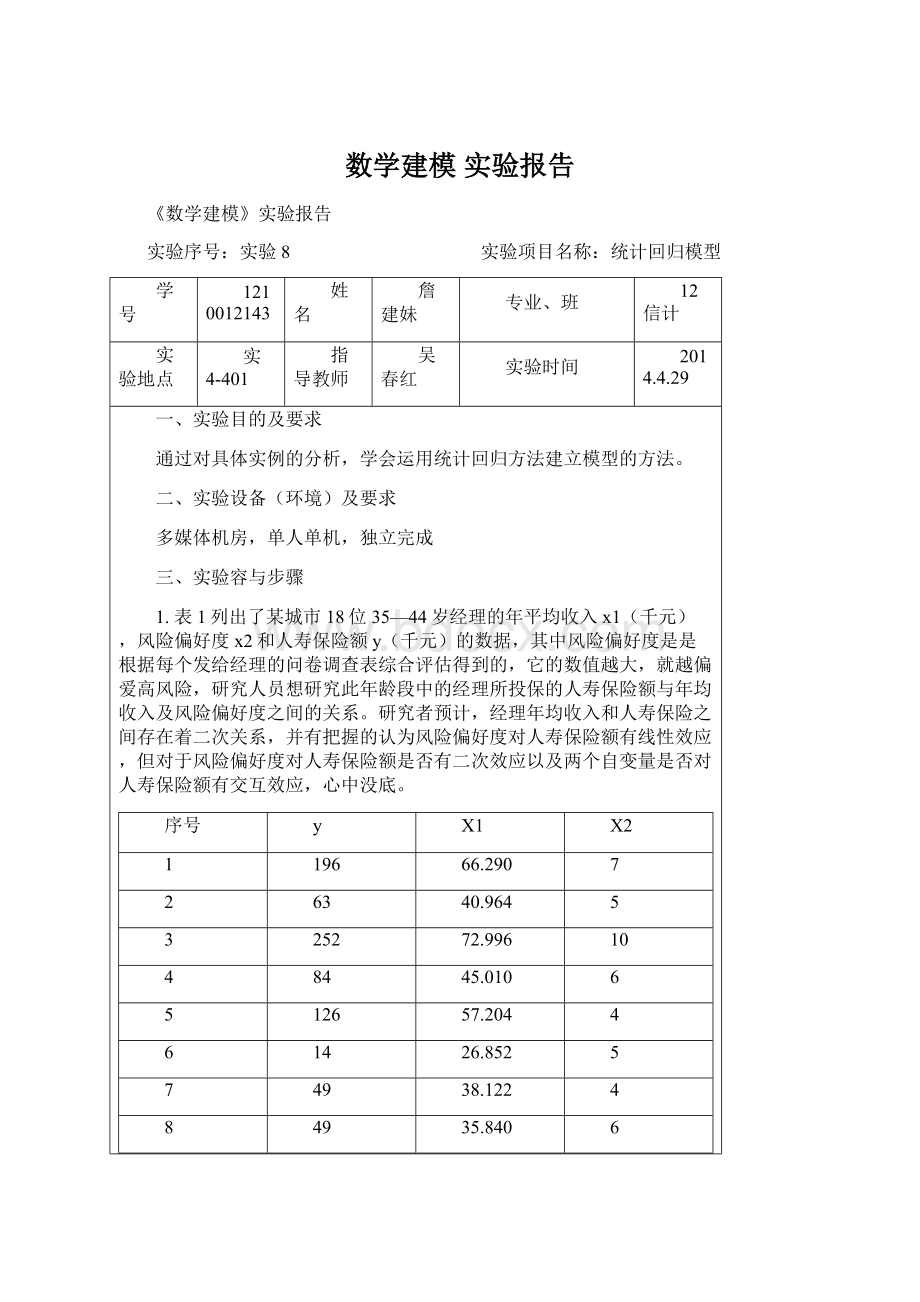
1.表1列出了某城市18位35—44岁经理的年平均收入x1（千元），风险偏好度x2和人寿保险额y（千元）的数据，其中风险偏好度是是根据每个发给经理的问卷调查表综合评估得到的，它的数值越大，就越偏爱高风险，研究人员想研究此年龄段中的经理所投保的人寿保险额与年均收入及风险偏好度之间的关系。

研究者预计，经理年均收入和人寿保险之间存在着二次关系，并有把握的认为风险偏好度对人寿保险额有线性效应，但对于风险偏好度对人寿保险额是否有二次效应以及两个自变量是否对人寿保险额有交互效应，心中没底。

序号

y

X1

X2

1

196

66.290

7

2

63

40.964

5

3

252

72.996

10

4

84

45.010

6

5

126

57.204

4

6

14

26.852

5

7

49

38.122

4

8

49

35.840

6

9

266

75.796

9

10

49

37.408

5

11

105

54.376

2

12

98

46.186

7

13

77

46.130

4

14

14

30.366

3

15

56

39.060

5

16

245

79.380

1

17

133

52.766

8

18

133

55.916

6

2.某公司想用全行业的销售额作为自变量来预测公司的销售额，下表给出了1977-1981年公司销售额和行业销售额的分季度数据（单位：

百万元）。

（1）画出数据的散点图，观察用线性回归模型拟合是否合适。

（2）建立公司销售额对全行业销售额的回归模型，并用DW检验诊断随机误差项的自相关性。

（3）建立消除了随机误差项自相关性后的回归模型。

年

季

t

公司销售额y

行业销售额x

1977

1

1

20.96

127.3

2

2

21.4

130

3

3

21.96

132.7

4

4

21.52

129.4

1978

1

5

22.39

135

2

6

22.76

137.1

3

7

23.48

141.2

4

8

23.66

142.8

1979

1

9

24.1

145.5

2

10

24.01

145.3

3

11

24.54

148.3

4

12

24.3

146.4

1980

1

13

25

150.2

2

14

25.64

153.1

3

15

26.36

157.3

4

16

26.98

160.7

1981

1

17

27.52

164.2

2

18

27.78

165.6

3

19

29.24

168.7

4

20

28.78

171.7

四、实验结果与数据处理

1.

Matlab代码：

>>X1=[66.29040.96472.99645.01057.20426.85238.12235.84075.79637.40854.37646.18646.13030.36639.06079.38052.76655.916];

>>Y=[19663252841261449492664910598771456245133133];

>>X=[ones（18,1）X1'（X1.^2）'];

>>[b,bint,r,rint,stats]=regress（Y',X）

处理结果：

b=

-60.5239

1.7886

0.0302

bint=

-143.459822.4121

-1.47425.0513

0.00020.0603

r=

5.0447

-0.4989

20.7987

2.7433

-14.7658

4.6881

-2.6174

6.5692

17.1895

0.2908

-21.1635

11.3961

-9.3474

-7.6785

0.5151

-27.0424

14.9336

-1.0552

rint=

-22.612332.7016

-29.015128.0174

-3.015144.6125

-25.584231.0708

-41.296111.7646

-17.452926.8291

-30.976325.7415

-21.246234.3845

-6.057940.4368

-28.030128.6116

-46.28273.9558

-16.144438.9366

-37.140918.4462

-33.074417.7174

-27.950728.9809

-42.7681-11.3167

-11.649441.5167

-28.886526.7760

stats=

0.9747289.19340.0000182.0773

参数

参数参考值

参数置信区间

B0

-60.5239

[-143.4598,22.4121]

B1

1.7886

[-1.4742,5.0513]

B2

0.0302

[0.0002,0.0603]

R²=0.9747F=289.1934p<0.0000s²=182.0773

由于置信水平a=0.05,处理结果p=0.00,p<0.05

R²=0.9747，指因变量Y的97.47%可由模型确定，Y与X1存在二次关系。

所以得到回归模型：

Y=0.5239+1.7886*X1+0.0302*X1^2;

结果表明年均收入和人寿保险额之间存在二次关系。

接下来处理两个自变量X1,X2对Y是否有交互效应。

因为Y与X1之间存在二次关系，所以我们设

Matlab代码：

>>X1=[66.29040.96472.99645.01057.20426.85238.12235.84075.79637.40854.37646.18646.13030.36639.06079.38052.76655.916];

>>X2=[7510645469527435186];

>>Y=[19663252841261449492664910598771456245133133];

>>X=[ones（18,1）X2'X1'（X1.^2）'];

>>[b,bint,r,rint,stats]=regress（Y',X）

处理结果：

b=

-62.3489

5.6846

0.8396

0.0371

bint=

-73.5027-51.1952

5.26046.1089

0.39511.2840

0.03300.0412

r=

-0.0512

0.3076

-1.3718

-0.6730

-3.7605

-1.3560

2.7129

-0.4817

0.5130

-0.3725

0.6842

2.6781

-1.0293

-0.3930

0.5561

1.3578

2.3248

-1.6456

rint=

-3.77913.6766

-3.53244.1475

-4.41241.6688

-4.46773.1217

-6.6500-0.8710

-4.21441.5023

-0.73446.1602

-4.21493.2516

-2.61833.6443

-4.18403.4390

-2.64474.0132

-0.72176.0779

-4.73962.6810

-3.81323.0272

-3.26764.3798

-0.46373.1793

-1.03585.6855

-5.26851.9773

stats=

1.0e+04*

0.00011.10700.00000.0003

B0

38.7434

[59.7383,137.2251]

B1

13.5218

[3.3538.30.3975]

R²=0.2%F=2.9p=0.0001s²=5721

参数

参数参考值

参数置信区间

-62.3489

[-73.5027,-51.1952]

5.6846

[5.2604,6.1089]

0.8396

[0.39511.2840]

0.0371

[0.03300.0412]

1.00

1107.0

0.00

0.0003

1.00指因变量Y可由X1与X2100%确定，F远远小于F的检验的临界值，p远小于a,

…

的系数均在置信区间。

可知Y与X1,X2有交互效应

Y=-62.3489+5.6846X2+0.8396X1+0.0371X1^2

2.

（1）散点图

由散点图可看出x与y存在线性相关，可用线性回归模型拟合。

（2）由散点图可看出，x与y存在正相关，所以使用一次回归模型

Matlab代码：

>>y=[20.960021.400021.960021.520022.390022.760023.480023.660024.100024.010024.540024.300025.000025.640026.360026.980027.520027.780029.240028.7800];

>>x=[127.3130132.7129.4135137.1141.2142.8145.5145.3148.3146.4150.2153.1157.3160.7164.2165.6168.7171.7];

>>[b,bint,r,rint,stats]=regress（y',X）

处理结果：

b=

-2.2816

0.1822

bint=

-3.4309-1.1324

0.17450.1900

r=

0.0447

-0.0073

0.0607

0.2220

0.0716

0.0589

0.0318

-0.0798

-0.1318

-0.1853

-0.2020

-0.0958

-0.0882

0.0233

-0.0220

-0.0216

-0.1193

-0.1145

0.7807

-0.2260

rint=

-0.38860.4780

-0.44860.4340

-0.38590.5072

-0.20300.6470

-0.37910.5222

-0.39560.5134

-0.42830.4918

-0.53960.3800

-0.58980.3262

-0.63840.2677

-0.65360.2496

-0.55630.3647

-0.54880.3723

-0.43760.4843

-0.47860.4346

-0.47270.4296

-0.55910.3204

-0.55100.3221

0.61320.9481

-0.63150.1794

stats=

1.0e+03*

0.00102.43810.00000.0000

参数

参数参考值

参数置信区间

-2.2816

[-3.4309,-1.1324]

0.1822

[0.1745,0.1900]

R²=1.00F=243.81p=0.000s²=0.000

R²=1.00，可知因变量y公司销售额的100%可由模型确定，F值远远超过检验的临界值，p远小于a=0.05,因而我们所建立的模型可用，y公司销售额与x行业销售额之间关系：

y=-2.2816+0.1822x.

五、分析与讨论

六、教师评语

签名：

日期：

成绩