《乘法公式的再认识因式分解》第2课时教案doc.docx

《乘法公式的再认识因式分解》第2课时教案doc.docx

《《乘法公式的再认识因式分解》第2课时教案doc.docx》由会员分享，可在线阅读，更多相关《《乘法公式的再认识因式分解》第2课时教案doc.docx（9页珍藏版）》请在冰豆网上搜索。

《乘法公式的再认识因式分解》第2课时教案doc

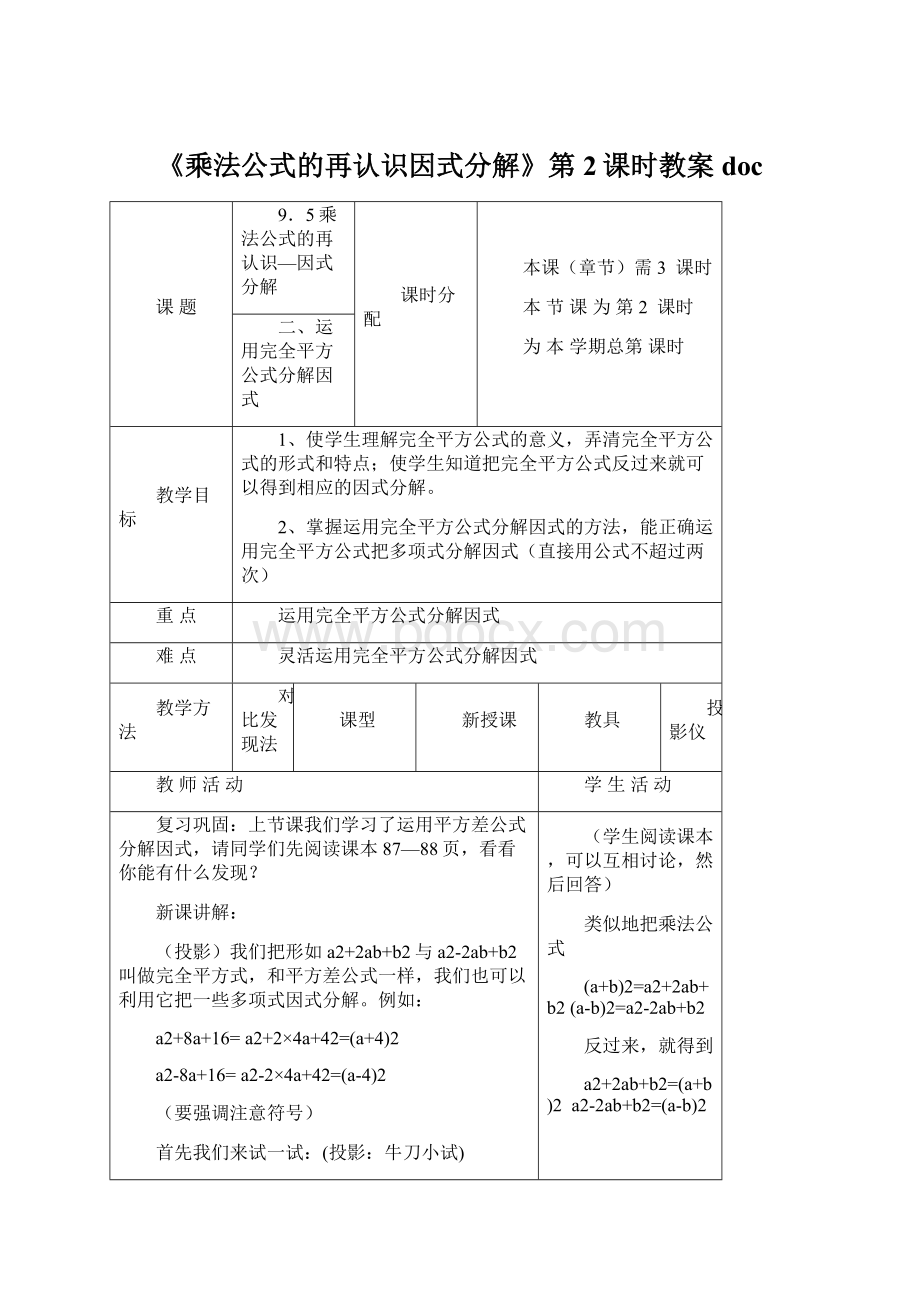
课题

9．5乘法公式的再认识—因式分解

课时分配

本课（章节）需3课时

本节课为第2课时

为本学期总第课时

二、运用完全平方公式分解因式

教学目标

1、使学生理解完全平方公式的意义，弄清完全平方公式的形式和特点；使学生知道把完全平方公式反过来就可以得到相应的因式分解。

2、掌握运用完全平方公式分解因式的方法，能正确运用完全平方公式把多项式分解因式（直接用公式不超过两次）

重点

运用完全平方公式分解因式

难点

灵活运用完全平方公式分解因式

教学方法

对比发现法

课型

新授课

教具

投影仪

教师活动

学生活动

复习巩固：

上节课我们学习了运用平方差公式分解因式，请同学们先阅读课本87—88页，看看你能有什么发现？

新课讲解：

（投影）我们把形如a2+2ab+b2与a2-2ab+b2叫做完全平方式，和平方差公式一样，我们也可以利用它把一些多项式因式分解。

例如：

a2+8a+16=a2+2×4a+42=（a+4）2

a2-8a+16=a2-2×4a+42=（a-4）2

（要强调注意符号）

首先我们来试一试：

（投影：

牛刀小试）

1.把下列各式分解因式：

（1）x2+8x+16;;

（2）25a4+10a2+1

（3）（m+n）2-4（m+n）+4

（教师强调步骤的重要性，注意发现学生易错点，及时纠正）

2把81x4-72x2y2+16y4分解因式.

（本题用了两次乘法公式，难度稍大，教师要鼓励学生大胆尝试，敢于创新）

将乘法公式反过来就得到多项式因式分解的公式。

运用这些公式把一个多项式分解因式的方法叫做运用公式法。

练习：

第88页练一练第1、2题

小结：

这节课你学到了什么知识，掌握什么方法？

教学素材：

A组题：

1、9x2-30xy+（3x-）2

2、把下列各式分解因式：

（1）x2y2-xy+1

（2）a2+a+¼

（3）、4-12（a-b）+9（b-a）2

B组题：

1、若

是完全平方式，则m的值是（）

（A）3（B）4（C）12（D）±12

2、已知

，

，则

的值是（）。

（A）1（B）4（C）16（D）9

3、把下列各式分解因式：

（1）、

（2）、1-x2+4xy-4y2

（学生阅读课本，可以互相讨论，然后回答）

类似地把乘法公式

（a+b）2=a2+2ab+b2（a-b）2=a2-2ab+b2

反过来，就得到

a2+2ab+b2=（a+b）2a2-2ab+b2=（a-b）2

学生上台板演：

解：

（1）x2+8x+16

=x2+2×4x+42

=（x+4）2

（2）25a4+10a2+1

=（5a2）2+2×5a2+1

=（5a2+1）2

（3）（m+n）2-4（m+n）+4

=（m+n）2-2×2（m+n）+22

=[（m+n）-2]2

=（m+n-2）2

解:

81x4-72x2y2+16y4

=9x2-2·9x2·4y2+（4y2）2

=（9x2-4y）2

=[（3x+2y）（3x-2y）]2

=（3x+2y）2（3x-2y）2

师生阅读88页

学生归纳总结

作业

第92页第2

（1）②④（3）①③题

板书设计

复习例3板演

………………

………………

……例4……

………………

………………

教学后记

课题

9．5乘法公式的再认识—因式分解

课时分配

本课（章节）需3课时

本节课为第1课时

为本学期总第课时

一、运用平方差公式分解因式

教学目标

1、使学生了解运用公式来分解因式的意义。

2、使学生理解平方差公式的意义，弄清平方差公式的形式和特点；使学生知道把乘法公式反过来就可以得到相应的因式分解。

3、掌握运用平方差公式分解因式的方法，能正确运用平方差公式把多项式分解因式（直接用公式不超过两次）

重点

运用平方差公式分解因式

难点

灵活运用平方差公式分解因式

教学方法

对比发现法

课型

新授课

教具

投影仪

教师活动

学生活动

情景设置：

同学们，你能很快知道992-1是100的倍数吗？

你是怎么想出来的？

（学生或许还有其他不同的解决方法，教师要给予充分的肯定）

新课讲解：

从上面992-1=（99+1）（99-1），我们容易看出,这种方法利用了我们刚学过的哪一个乘法公式?

首先我们来做下面两题：

（投影）

1.计算下列各式:

（1）（a+2）（a-2）=;

（2）（a+b）（a-b）=;

（3）（3a+2b）（3a-2b）=.

2．下面请你根据上面的算式填空:

（1）a2-4=;

（2）a2-b2=;

（3）9a2-4b2=;

请同学们对比以上两题，你发现什么呢？

事实上，像上面第2题那样，把一个多项式写成几个整式积的形式叫做多项式的因式分解。

（投影）

比如：

a2–16=a2–42=（a+4）（a–4）

例题1：

把下列各式分解因式；（投影）

（1）36–25x2;

（2）16a2–9b2;

（3）9（a+b）2–4（a–b）2.

（让学生弄清平方差公式的形式和特点并会运用）

例题2：

如图，求圆环形绿化区的面积

练习：

第87页练一练第1、2、3题

小结：

这节课你学到了什么知识，掌握什么方法？

教学素材：

A组题：

1．填空：

81x2-=（9x+y）（9x-y）;

=

利用因式分解计算：

=。

2、下列多项式中能用平方差公式分解因式的是（）

（A）

（B）

（C）

（D）

3.把下列各式分解因式

（1）1-16a2

（2）9a2x2-b2y2

（3）.49（a-b）2-16（a+b）2

B组题：

1分解因式81a4-b4=

2若a+b=1,a2+b2=1,则ab=;

3若26+28+2n是一个完全平方数，则n=.

由学生自己先做（或互相讨论），然后回答，若有答不全的，教师（或其他学生）补充．

学生回答1：

992-1=99×99-1=9801-1

=9800

学生回答2：

992-1就是（99+1）（99-1）即100×98

学生回答:

平方差公式

学生回答:

（1）:

a2-4

（2）:

a2-b2

（3）:

9a2-4b2

学生轻松口答

（a+2）（a-2）

（a+b）（a-b）

（3a+2b）（3a-2b）

学生回答:

把乘法公式

（a+b）（a-b）=a2-b2

反过来就得到

a2-b2=（a+b）（a-b）

学生上台板演：

36–25x2=62–（5x）2

=（6+5x）（6–5x）

16a2–9b2=（4a）2–（3b）2

=（4a+3b）（4a–3b）

9（a+b）2–4（a–b）2

=[3（a+b）]2–[2（a–b）]2

=[3（a+b）+2（a–b）]

[3（a+b）–2（a–b）]

=（5a+b）（a+5b）

解：

352π–152π

=π（352–152）

=（35+15）（35–15）π

=50×20π

=1000π（m2）

这个绿化区的面积是

1000πm2

学生归纳总结

作业

第91页第1

（1）

（2）②③（3）①③④题

板书设计

复习例1板演

………………

………………

……例2……

………………

………………

教学后记

课题

第9章从面积到乘法公式

课时分配

本课（章节）需2课时

本节课为第2课时

为本学期总第课时

9.4乘法公式

（2）

教学目标

1.正确熟练的运用乘法公式进行混合运算和简化的计算

2.在应用公式的过程中，提高变形应用公式的能力

重点

正确熟练的运用乘法公式进行混合运算和简化的计算

难点

能够在运用公式计算中，提高变形应用公式的能力

教学方法

讲练结合、探索交流

课型

新授课

教具

投影仪

教师活动

学生活动

情景设置：

回忆上节课所学的乘法公式：

=

这节课我们利用乘法公式解决实际问题

新课讲解：

例1：

用乘法公式计算

⑴

；⑵

；

⑶

；⑷

例2：

计算

⑴

；⑵

；

⑶

；⑷　[（a-b）2-（a+b）2]2

能够根据实际情况灵活运用乘法公式解题。

课堂练习：

P82练一练1、2、3、4

数学实验室：

制作若干张长方形和正方形硬纸片，通过图形计算（a+b+c）2的公式，并通过运算推导这个公式。

练习：

已知3（a2+b2+c2）=（a+b+c）2，求证:

a=b=c

小结：

能够根据题目的要求灵活的运用乘法公式。

教学素材：

A组题：

1．利用乘法公式进行计算：

（1）（x-1）（x+1）（x2+1）（x4+1）　　

（2）（3x+2）2-（3x-5）2　　

（3）（x-2y+1）（x+2y-1）

（4）（2x+3y）2（2x-3y）2　　　

（5）（2x+3）2-2（2x+3）（3x-2）+（3x-2）2

（6）（x2+x+1）（x2-x+1）　　　

2.已知a+b=-2,ab=-15求a2+b2.

B组题：

1.若（x2+px+8）（x2-3x+q）的积中不含有x3和x2项，求p,q的值

2.已知

，求⑴

，⑵　

3.试求（2-1）（2+1）（22+1）（24+1）…（232+1）+1的个位数字

4.a+b=5,ab=3，求：

（1）（a-b）2；

（2）a2+b2；（3）a4+b4

5.观察下列各式（x-1）（x+1）=x2-1，（x-1）（x2+x+1）=x3-1，（x-1）（x3+x2+x+1）=x4-1，根据前面各式的规律可得（x-1）（xn+xn–1+…+x+1）=。

学生回答

由学生自己先做（或互相讨论）

板演

教师与同学共同订正

学生讨论

共同总结

作业

第83页3、5、6

板书设计

复习例1板演

………………

………………

……例2……

………………

………………

教学后记