南通市二模数学试题及答案.docx

南通市二模数学试题及答案.docx

《南通市二模数学试题及答案.docx》由会员分享，可在线阅读，更多相关《南通市二模数学试题及答案.docx（23页珍藏版）》请在冰豆网上搜索。

南通市二模数学试题及答案

则an

ai2%

江苏省南通市2020届高三第二次模拟考试数学试题

一、填空题：

本大题共14小题，每小题5分，共70分.

1.曲线yx32x在点（1,—1）处的切线方程是▲.

2.若1~5i-abi（a,bR,i为虚数单位），则ab=▲.

3i

3.命题“若实数a满足a&2,则a24”的否命题是▲命题（填“真”、"假”

之一）.

4.把一个体积为27cm3的正方体木块表面.涂上红漆，然后锯成体积为1cm3的27个小正方体，现

从中任取一块，则这一块至少有一面涂有红漆的概率为▲.

5.某教师出了一份三道题的测试卷，每道题1分，全班得3分、2分、1分和0分的学生所占比例

分别为30%、50%、10%和10%,则全班学生的平均分为▲分.

6.设Maa（2,0）m（0,1）,mR和

Nbb（1,1）n（1,1）,nR都是元素为向量的集

合，贝UMHN=▲.

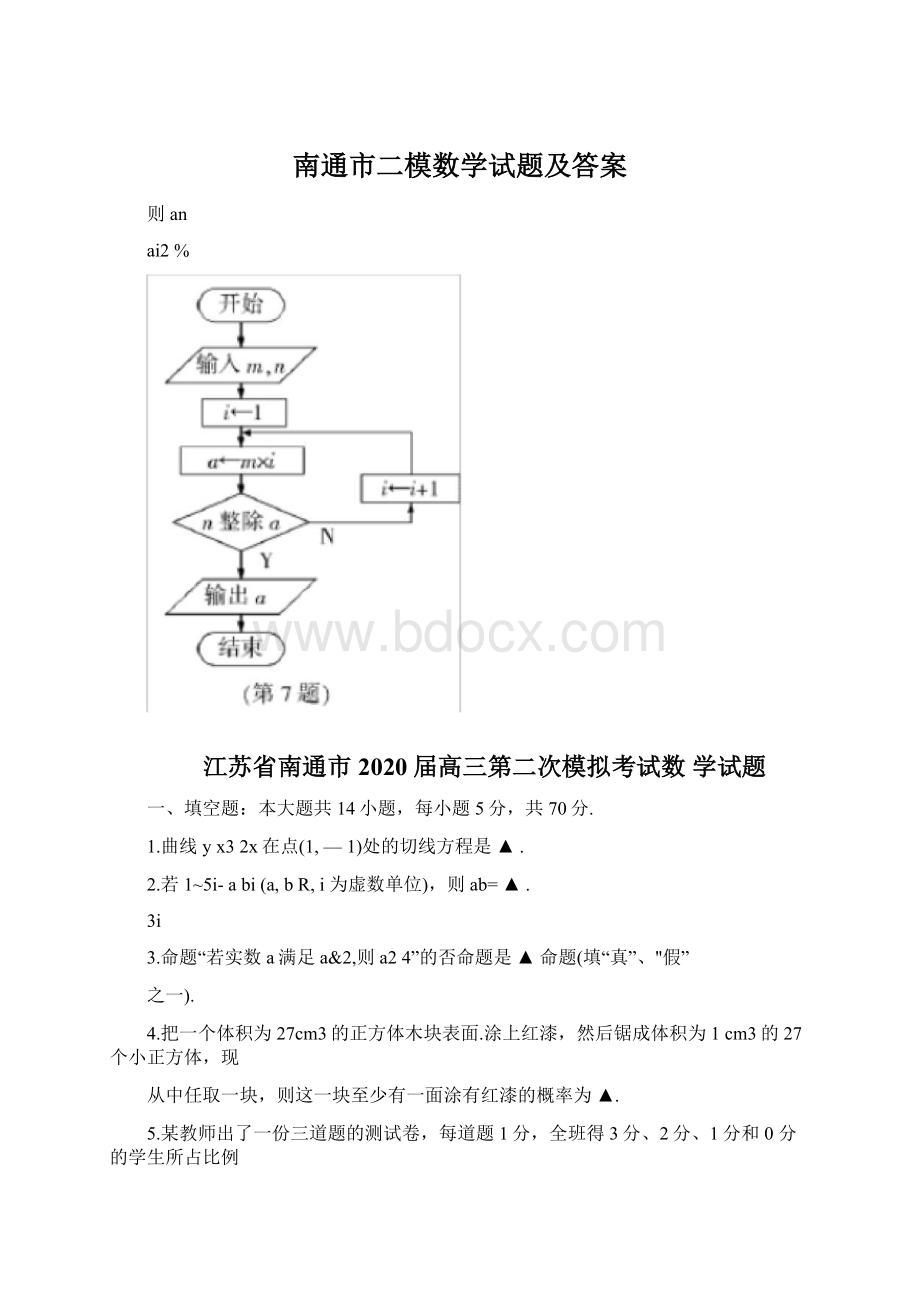
7.在如图所示的算法流程图中，若输入m=4,n=3,则输出的

a=▲.

8.设等差数列an的公差为正数，若

a1a2a315,a1a2a380,

9.设，是空间两个不同的平面，mn是平面及外的两条不同直线.从“①m

，n；②!

；③n，；④mil”中选取三个作为条件，余下一个作为结论,

写出你认为正确的一个命题：

▲（用代号表示）.

10一.定义在R上的函数f（x）满足：

f（x）=f（x+2）,当x3,5时，f（x）=2-x-4.下

列四个

不等关系

f（sin6）f（cos1）；

f（cos2）>f（sin2）.

其中正确的个数是▲.

2

11.在平面直角坐标系xOy中，已知A、B分别是双曲线x2X1的左、右焦点,

3

△ABC的顶点

C在双曲线的右支上,,则sinAsinB的值是▲

sinC

12.在平面直角坐标系xOy中，设点P（x1,yj、

Q（x2,V2）,定义：

d（P,Q）=xi-旭+y1-y2.已

知点B（1,0）,点M为直线x-2y+2=0上的动点，则使d（B,M）取最小值时点M

的坐标是

▲

13.若实数x,y,z,

14.在平面直角坐标系

t满足1WxWy

yt

xOy中，设A、BC是圆x2+y2=1上相异三点，若存在正实

数，，使得

uuruuu

OC=OA

uuu

OB，

32的取值范围是—▲

1.x—y—2=0

2.

8

25

3.

4.

26

27

5.2

6.

2,0

7.12

8.

105

9.①③④②（或②③④①）

10.1

11.

1

2

13.表

14.2,

12.1,3

2

二、解答题：

本大题共6小题「，共计90分，解答时应写出文字说明，证明过程或演算步骤.

15.（本小题满分14分）

如图，平面PAC平面

ABC，点E、F、。

分别为线段PA

PBAC的中点，点G

是线段CO

的中点，ABBCAC

4,PAPC272.求证:

（1）PA平面EBO；

（2）FG//平面EBO.

【证明】由题意可知,

ABC为等边三角形.

（1）因为O为边AC的中点，所以BOAC,

P

PAC为等腰直角三角形，

A

2分

B

（第15题）

C

因为平面PAC平面ABC,平面PACI平面ABCAC,

BO平面ABC,所以BO面PAC.

因为PA平面PAC,所以BOPA,

在等腰三角形PAC内，O,E为所在边的中点，所以OEPA,

又BOIOEO,所以PA平面EBO;

（2）连AF交BE于Q,连QO

A

因为E、F、O分别为边PAPBPC的中点，

所以AO

OG

2,且Q是4PAB的重心,

P

8

F

Q

C

10分

B

12分

于是QQ

2OO，所以FG//QO.

因为FG平面EB「O,QO

平面EBO,

所以FG//平面

14分

【注】第

（2）小题亦可通过取PE中点H,利用平面FGH//平面EBOE得.

16.（本小题满分14分）

已知函数f（x）2cos垓3cos或sin2

（i）设2,2,且f（）避i,求的值;

（2）在△ABC中，AB=1,

f（C）用1,且△ABC的面积为济

sinA+sinB

的值.

【解】

（1）f（x）

2x

23cos一

2

xx

2sin—cos—=3（1cosx）sinx=2cos

jr

6

2cosx

兀

cosx芳6

兀

2k兀一（k

3

Z）

2或6・

因为△ABC勺面积为

，所以手

-absin-,于是ab273.26,

在△AB外,设内角

B的对边分别是a,b.

由余弦定理得1a2

b2

兀

2abcos-6

b26,所以

3,

2.

2,一

「或

3

由正弦定理得春呼华

sinAsinB1ab1—3

22

14

分

17.（本小题满分14分）

2..2

在平面直角坐标系xOy中，如图，已知椭圆E:

与当1（ab0）的左、右顶点b

分别为A、A2,

上、下顶点分别为B1、B2.设直线AB的倾斜角的正弦值为1,圆C与以线段OA2

3

为直径的圆

关于直线AiBi对称.

（1）求椭圆E的离心率;

（2）判断直线与圆C的位置关系，并说明理由;

Ai

B2

（第17题）

A2fr-x

yy

B1

（3）若圆C的面积为,求圆C的方程.

【解】

（1）设椭圆E的焦距为2c（c>0）,

因为直线AB1的倾斜角的正弦值为1,所以♦b=

3,a2b2

于是a28b2,即a2

8（a2c2）,所以

E的离心

（2）由e

c2

14~4~

7_14

84

可设a4kk

于是AB1的方程为「：

x272y

4k

OA2

占

八、、

2k,0至ljAB

又以OA2为直径的圆的半径

「即有d

ABi

切.

（3）由圆C的面积为

知圆半径为1

P

P

C

S

D

设OA2的中点1,0关于直线AB：

x272y2。

的对称点为m,n,

如图，实线部分的月牙形公园是由圆P上的一段优弧和圆Q上的一段劣弧围成,

圆P和圆Q的

半径都是2km,点P在圆Q上，现要在公园内建一块顶点都在圆P上的多边形

活动场地.

（1）如图甲，要建的活动场地为△RST求场地的最大面积;

B

RT左边的部分是一个大小不超过半圆的弓形,

1

k

2

10分

12分

解得m1,n乎.所以，圆c的方程为x12y乎1.3333

14分

18.（本小题满分16分）

（2）如图乙，要建的活动场地为等腰梯形

ABCD求场地的最大面积.

A

RT与圆Q只能相

4分

RM

M

【解】

（1）如右图，过S作SHLRT于H,

n.2

m14

1,

2.2220.

T

（第17题甲）

（第17题乙）

由题意，ARST在月牙形公园里,

m1

2

Q

1一一

SarskSH2

RT.

WJ有RTC4,SHC2,

当且仅当

RT切圆Q于P时（如下左图），

上面两个不等式中等号同时成立.

场地面积的

大值为Sars=—42=4

2

（km2）.

最

（2）同

（1）的分析，要使得场地面积最大,

AD左边的部分是一个大小不超过

半圆的弓形，

AD必须切圆Q于P,再设/BPA二

O1

SH边形ABCD222sin2

2sin（兀

）4（sin

sin

cos）0

令ysin

ycos

11分

sincos

cos

cos

cos

sin（

sin

2cos2

cos

3'2

函数ysinsin

14分

cos在才处取到极大值也是最大值,

3

7t

场地面积取得最大值为36

（km2）.

19.（本小题满分16分）

设定义在区间［x

为坐标原点，设向

日uuu

重OA=x1?

fX

1,x2］上的函数

y=f（x）的图象为C,M是C上的任意一点，O

UUUU

OBx2,fx2

OMr=（x,y）,当实数人满足x=入x1+（1

—入）x2时，记向

uuur.uuu一uur

“函数y=f（x）在区间［x［，x2］上可在标准k下

量ON=入OA+（1—入）OB.定义

线性近似”是指

“Mn

（1）设函数f（x）=x2在区间［0,1］上可在标准k下线性近似，求k的取值范围;

（2）求证：

函数g（x）lnx在区间em,em1（mR）上可在标准k=1下线性近似.

8

（参考数据：

e=2.718,ln（e—1）=0.541）

【解】

ruuuruuu

（1）由ON=入OA+（1—

、uuruuruur

入）OB得至IBN=入BA,

占

八、、

线,

又由x=Xx1+（1—入）x2与向量Or尸入OA+（1—入）Or,得N与M的横坐标相

同.

对于［0,1］上的函数

y=x2,A（0,0）,B（1,1）,

则有

UULU

MN

1,,uuuu

1,故MN4

的

（2）

对于

上的函数ylnx,

A（

em,m

B（em1,m1）,8分

则直线AB的方程

ymm^1-m（xem）,10分

ee

1,mmm1

々h（x）Inxm—^m（xe）,具中xe,emR,

ee

于是

h（x）1nm-^1―m，

xee

・T3分

列表如下:

x

me

（mm+1m

m+1m

（m+1mm+）

m+1e

h'（x）

+

0

一

h（x）

0

增

h（em1em）

减

0

则|mn|hx,且在xem1em处取得最大值，

又h（em1em）lne1——-0.123-,从而命题成

e18

立.16分

20.（本小题满分16分）

已知数列｛an｝满足a〔a2Lann2（nN*）.

（1）求数列｛an｝的通项公式；

（2）对任意给定的kN*,是否存在p,rN*（kpr）使上，工，工成等差akapar

数列？

若存

在，用k分别表示p和r（只要写出一组）；若不存在，请说明理由；

（3）证明：

存在无穷多个三边成等比数列且互不相似的三角形，其边长为

an1,an2,an3.

【解】

（1）当n1时，a11;

当n>2,nN*时，a1a2Lan1（n1）2,

所以ann2（n1）22n1;

an2n1（nN*）.3分

（2）当k1时，若存在p,r使。

，工，工成等差数列，则1

akapara「apak2p1

因为p>2,所以a「0,与数列｛an｝为正数相矛盾，因此，当k1时不存

在；5分

当Q2时，设akx,apy,arz,则」12,所以z,7

xzy2xy

分

令y2x1,得zxyx（2x1）,此时akx2k1,apy2x12（2k1）1,

所以p2k1,arz（2k1）（4k3）2（4k25k2）1,

所以r4k25k2;

综上所述，当k1时，不存在p,r；当k42时，存在p2k1,r4k25k2满足题设.

10分

（3）作如下构造：

a.（2k3）2,a。

？

（2k3）（2k5）,a组（2k5）2,其中kN*,

它们依次为数列｛an｝中的第2k26k5项，第2k28k8项，第2k210k13

项，……12分

显然它们成等比数列，且a,an2a%,a.a©a%,所以它们能组成三角形.

由kN*的任意性，这样的三角形有无穷多个.14分

下面用反证法证明其中任意两个三角形AB©和A2B2c2不相似：

若三角形AB£和A2B2c2相似，且Ik2,则（2k13）（2k125）（2k23）（2k225）,

（2匕3）（2k23）

整理得空一处」，所以％k2,这与条件k1k2相矛盾，2k132k23

因此，任意两个三角形不相似.

故命题成

立.16

【注】1.第

（2）小题当ak不是质数时，p,r的解不唯一；

2.第（3）小题构造的依据如下：

不妨设nn2%,且an2,an3符合题意，则公比q>1,因aman2"，又a.a。

？

"，则1qq2,所以1q应」，因为三项均为整数，所以q为1,近」内的既约分

22

数且a。

含平方数因子，经验证，仅含12或32时不合，所以2*

an1（2k3）2p（k,pN）;

3.第（3）小题的构造形式不唯一.

A.选修4—1:

几何证明选讲

又M为PA的中点，所以

2

MPMB

BMP

PMC

A

数学II（附加题）

21.【选做题】本题包括A,B,C,D四小题，请选定其中两题作答，每小题10分,共计20分,

解答时应写出文字说明，证明过程或演算步骤.

自圆O外一点P引圆的一条切线PA切点为A,M为PA的中点过点M引圆。

的割线交该圆于B、C两点，且/BMP=100,

/BPC=40,求/MPB的大小.

MBMC.

【解】因为MA*圆。

的切线，所以MA

BM2PMC.

于是MPBMCP.

在AMCP中

MPB

MCP

BPCBMP

180

10分

B.选修4—2:

矩阵与变换

....ab

已知二阶矩阵A

cd

矩阵A属于特征值

1的一个特征向量为

属于特征值

24的一个特征向量为

3--

22.求矩阵A

3a

同理可得3c

2b

2d

12,

8,

解得a2,

3,c

2,d1

10分

C.选修4—4:

坐标系与参数方程

在平面直角坐标系xOy中，已知曲线C的参数方程为

2cos'为参数.以sin

直角坐标系原

点。

为极点，x轴的正半轴为极轴建立极坐标系，直线

l的极坐标方程为

cos42点•点

P为曲线C上的动点，求点P到直线l

距离的最大值.

【解】cos92点化简为

4

cos

设点P的坐标为2cos,sin

得P到直线l的距离d

2cossin

卜5sin

2

1

cos——,sin

5

sin

-1

d2,2_10

dmax2"2.

2

D.选修4—5:

不等式选讲

若正数a,b,c满足a+b+c=1,

【解】因为正数

3a23b2

1

3c2

即

3a2

1

3b2

当且仅

当3a

求,

3a2

1

3b2

」的最小值.

3c2

a,b,c满足a+b+c=1,

以

3a23b23c2

231323c2,即ab

1

1时，原式取

3

【必做题】第22题、第23题，每题i0分，共计20分.解答时应写出文字说明,证明过程或演算步骤.

22.

在正方体ABCDAiBiCiDi中，。

是AC的中点，E是线段DO上一点，且DE=入EO.

（i）若入=i,求异面直线DE与CD所成角的余弦值;

（2）若平面CDEL平面CDO,求人的值.

Ci

uuruur1

【解】（i）不妨设正万体的棱长为i,以DA,DC,DDi

为单位正交基底建立如图所示的空间直角坐标系

则A（i,0,0）,

iin

2,2,0

C0,i,

，D（0,

Er

于是

4

uuirDE

Di

mjir

Ai

E

Dxyz

C

O

B

（第22题）

0,I）,

D

uuuu

，CDi

0,

i,i.

cos

uurrnuu

DE,CDi

uurjuju

DECDiuUTTUUr=

|DE||CDi|

（2）

异面直线AE

设平面CDO的向量为m=（xi,

yi,

CD所

成角的余弦值

、「jjjt-

zi）,由m・co=0,

m-CDr=0

i）.

ii八

2xi2yi0,

yizi0,

取Xi=i

yi=Zi=i,

即m=（i,i

由DE=入EQ贝UE,,

2（i）2（i）

JUT

，DE=

又设平面CDE勺法向量为n=（X2,y2,Z2）,由n•

2（i

uur

CD

=0,

——12（i）i

UJLT

n,DE=0.

y20

入，

即n=（—2,0,入）.

得X2y2Z2取X2=2,彳4z2=一

2（i）2（i）i°’

因为平面CDEX平面CDF,所以

2.

23.一种抛硬币游戏的规则是：

抛掷一枚硬币.，每次正面向上得1分，反面向上得2分.

（1）设抛掷5次的得分为，求的分布列和数学期望E;

（2）求恰好得到n（nN*）分的概率.

5

【解】

（1）所抛5次得分的概率为P（=i尸c552（i=5,6,7,8,9,

10）,

其分布列如下:

5

6

7

8

9

10

P

1

5

5

5

5

1

32

32

16

16

32

32

105

E=ic551=15（分）.5分

i522

（2）令pn表示恰好得到n分的概率.不出现n分的唯一情况是得到n—1分以后再掷出一次反面.因为“不出现n分”的概率是1—pn,“恰好得到n—1分”的概率是Pn-1,

因为“掷一次出现反面”的概率是-,所以有1—Pn=1Pn_1,7

22

分

即Pn—2=—1Pn12.

323

于是Pn2是以P1—2=1—2=—1为首项，以一j为公比的等比数列.

n1n

所以Pn——=——1,即Pn=121.

362，产32

答：

恰好得到n分的概率是121.10分

32

12k4kl2k

3，