深圳市交通拥堵问题分析数学建模论文 精品.docx

深圳市交通拥堵问题分析数学建模论文 精品.docx

《深圳市交通拥堵问题分析数学建模论文 精品.docx》由会员分享，可在线阅读，更多相关《深圳市交通拥堵问题分析数学建模论文 精品.docx（30页珍藏版）》请在冰豆网上搜索。

深圳市交通拥堵问题分析数学建模论文精品

一摘要

本文主要针对深圳市交通拥堵问题进行分析。

首先，我们对深圳市整体道路网的建设及其发展趋势进行分析，以梅林关、布吉关等关口局部为例，对交通量进行分析，并建立模型，从多方面分析了造成深圳市交通拥堵的原因。

然后，在深圳市的城市功能分区对交通拥堵的原因研究中，采用了空间聚类方法分析城市功能分区的影响因素，并试图通过研究结果调整深圳市的城市功能分区来解决交通拥堵问题。

但数据有限，仅以部分区域进行了空间聚类方法说明。

最后，对解决深圳市交通拥堵问题给出合理建议。

最后，我们充分正视该模型的缺点，并对问题进行了进一步思考。

关键词深圳市交通拥堵城市功能区划缓解措施

二问题重述

近年来，随着国家经济的快速发展，特别是国家政策对汽车行业发展的扶持，小汽车保有量急剧增加。

另外城市化进程加快，但是交通基础设施建设跟不上，进一步加剧供需矛盾，由此我国各大中城市又出现了新一轮的交通拥堵，而且有进一步发展和恶化的趋势。

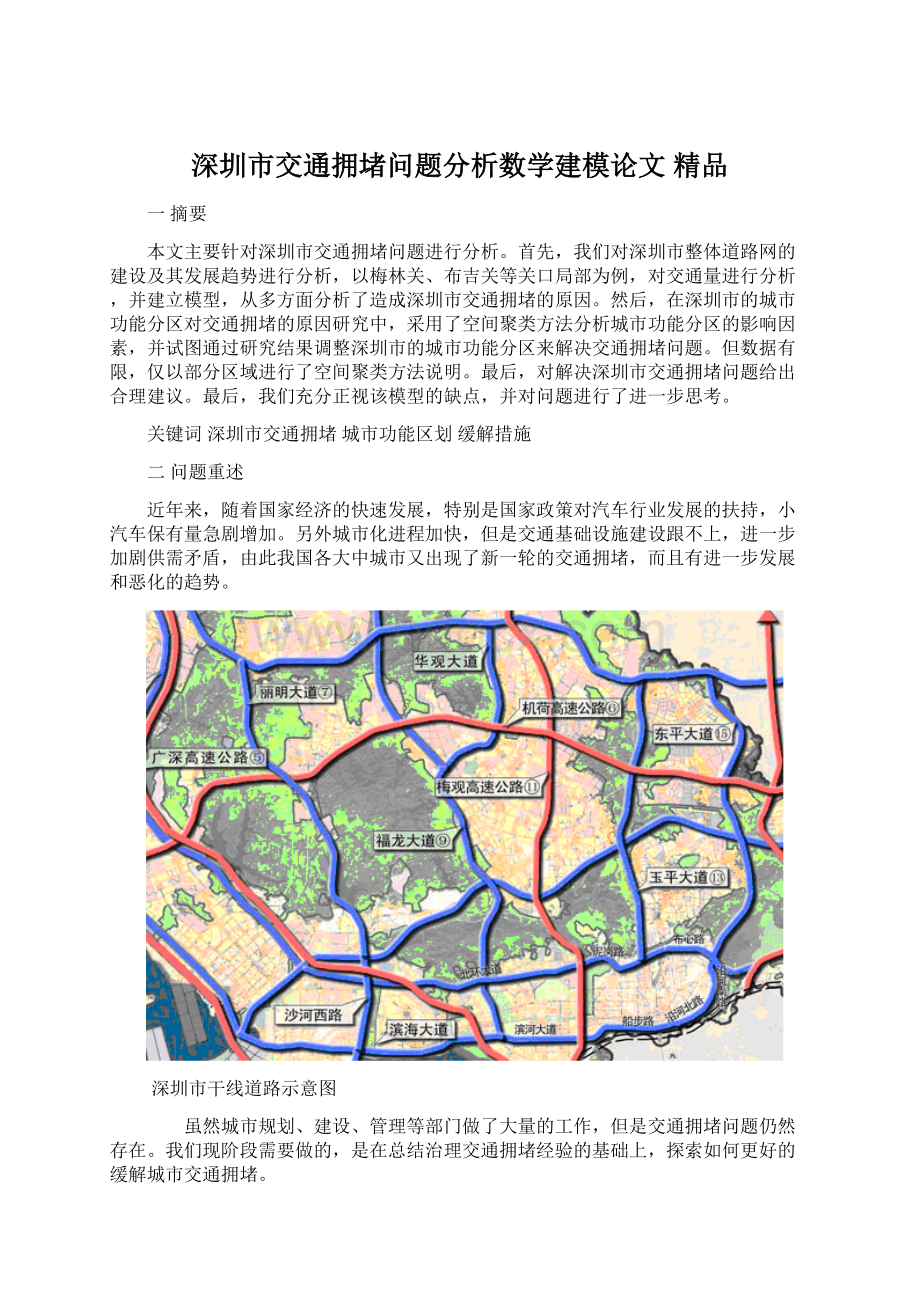
深圳市干线道路示意图

　　虽然城市规划、建设、管理等部门做了大量的工作，但是交通拥堵问题仍然存在。

我们现阶段需要做的，是在总结治理交通拥堵经验的基础上，探索如何更好的缓解城市交通拥堵。

表1：

北京、上海、天津、杭州、广州、深圳道路交通管理基础数据对比表

　　从上表可以看出，深圳的机动车密度高居全国之首，为了缓解交通拥堵，深圳采取了一系列交通管理措施，政府在道路建设上也投入了大量的资金。

这些措施一定程度上代表了国内大多城市在解决交通拥堵中的普遍做法，但是并没有从根本上解决深圳市交通拥挤的问题。

针对这一矛盾，我们主要研究以下三个问题：

（1）以梅林关为例，通过对深圳市路网结构和已知数据的研究，分析造成深圳市交通拥堵的深层原因，并对研究以后的交通拥堵问题应采集的数据提出建议。

（2）对深圳市的城市功能区划进行解剖，分析其造成拥堵的原因，通过合理的功能分区，提出建议来解决拥堵问题。

（3）针对拥堵问题提出合理的措施，主要包含两个方面，一是在交通管控方面采取措施，二是通过经济杠杆手段调整汽车供求关系，三是增建道路来缓解交通拥堵问题。

三模型的基本假定

（1）不考虑交通事故造成的影响，遇到交通事故时能及时处理；

（2）只考虑市内交通状况，排除外地车辆的出入对问题的干扰;

（3）步行人流和自行车流对交通拥堵的影响不大，在简化模型时刻不考虑；）uxingrenliu大量的资金市在解决交通拥堵中的普遍做法。

________________________________________________________________________________________________

（4）假设市内的道路状况良好，没有房屋的拆迁、道路桥梁的维修和破坏，没有道路的管制通行和占道；

（5）不考虑火车、飞机等交通运输方式对问题的影响

四符号的规定及名词解释

P————小汽车价格

Q————小汽车需求量

x————时间（小时）

——驾驶员反应时间

——汽车通过十字路口的时间。

——停车距离的驾驶时间。

n——拥堵指数（一天中交通量超过平均交通量的时间与24的比值。

）yongdu____________________________________________________________________________________________________________

aver——平均交通量。

五分析、建立模型并进行求解

A对交通拥堵原因进行分析

我们通过对梅林关道路网的分析，简化出如图所示的关口处的道路简图，并以此为分析对象，建立关口交通量的模型。

首先我们对进出该关口间的各道路交通量进行分析，利用Matlab对交通量进行定量化的分析，给出了个路口的交通量随时间的变化规律，并以高峰时段的交通量为代表进行验算，如下所示，

根据Matlab曲线拟合功能可以得到关口个断面的交通量随时间的函数关系，公式如下：

序号

断面

公式

断面经纬度坐标

1

107国道（广深公路）南头检查站南行-北-战略

LinearmodelPoly6:

f（x）=p1*x^6+p2*x^5+p3*x^4+p4*x^3+p5*x^2+

p6*x+p7

Coefficients（with95%confidencebounds）:

p1=-0.0007755（-0.004703,0.003152）

p2=0.02934（-0.2426,0.3013）

p3=0.3453（-6.812,7.503）

p4=-29.26（-118.2,59.69）

p5=418.1（-106.5,942.7）

p6=-1564（-2842,-285.7）

p7=2772（1818,3727）

Goodnessoffit:

SSE:

3.959e+006

R-square:

0.937

AdjustedR-square:

0.9148

RMSE:

482.6

22.554515,113.908382

2

深南大道南头检查站出-南-战略

LinearmodelPoly6:

f（x）=p1*x^6+p2*x^5+p3*x^4+p4*x^3+p5*x^2+

p6*x+p7

Coefficients（with95%confidencebounds）:

p1=0.0001567（-0.005042,0.005356）

p2=-0.03443（-0.3944,0.3256）

p3=1.845（-7.63,11.32）

p4=-42.13（-159.9,75.61）

p5=427.6（-266.8,1122）

p6=-1330（-3022,361.7）

p7=1692（428.6,2956）

Goodnessoffit:

SSE:

6.936e+006

R-square:

0.8848

AdjustedR-square:

0.8441

RMSE:

638.8

22.549734,113.912108

3

G4（广深高速）（2260km+969m）南行-北-战略

LinearmodelPoly6:

f（x）=p1*x^6+p2*x^5+p3*x^4+p4*x^3+p5*x^2+

p6*x+p7

Coefficients（with95%confidencebounds）:

p1=-0.0004962（-0.002455,0.001463）

p2=0.02912（-0.1065,0.1647）

p3=-0.3273（-3.897,3.242）

p4=-10.22（-54.58,34.14）

p5=244.9（-16.7,506.5）

p6=-1202（-1840,-565.1）

p7=1814（1338,2290）

Goodnessoffit:

SSE:

9.844e+005

R-square:

0.9795

AdjustedR-square:

0.9723

RMSE:

240.6

22.584194,113.90963

4

广深高速同乐检查站出-东-战略

LinearmodelPoly6:

f（x）=p1*x^6+p2*x^5+p3*x^4+p4*x^3+p5*x^2+

p6*x+p7

Coefficients（with95%confidencebounds）:

p1=0.0003426（-0.001293,0.001978）

p2=-0.0442（-0.1574,0.06904）

p3=1.874（-1.106,4.854）

p4=-35.54（-72.58,1.491）

p5=304.3（85.93,522.7）

p6=-835.4（-1367,-303.3）

p7=681.8（284.3,1079）

Goodnessoffit:

SSE:

6.862e+005

R-square:

0.9394

AdjustedR-square:

0.918

RMSE:

200.9

22.57326,113.920045

5

沙河西路白芒关检查站出-南-战略

LinearmodelPoly6:

f（x）=p1*x^6+p2*x^5+p3*x^4+p4*x^3+p5*x^2+

p6*x+p7

Coefficients（with95%confidencebounds）:

p1=0.0002829（-0.001866,0.002432）

p2=-0.02771（-0.1765,0.1211）

p3=1.063（-2.853,4.979）

p4=-20.12（-68.79,28.55）

p5=180.8（-106.3,467.8）

p6=-516.6（-1216,182.6）

p7=423.4（-99.03,945.8）

Goodnessoffit:

SSE:

1.185e+006

R-square:

0.8381

AdjustedR-square:

0.7809

RMSE:

264

22.624308,113.939123

6

松白路白芒检查站入-北-战略

LinearmodelPoly6:

f（x）=p1*x^6+p2*x^5+p3*x^4+p4*x^3+p5*x^2+

p6*x+p7

Coefficients（with95%confidencebounds）:

p1=0.001111（-0.0006401,0.002862）

p2=-0.07967（-0.2009,0.04157）

p3=2.211（-0.9792,5.402）

p4=-30.5（-70.16,9.147）

p5=213.1（-20.7,447）

p6=-526.4（-1096,43.33）

p7=395.6（-30.01,821.3）

Goodnessoffit:

SSE:

7.866e+005

R-square:

0.898

AdjustedR-square:

0.862

RMSE:

215.1

22.630545,113.935135

7

福龙隧道-南向北行驶

22.565104,114.017562

8

福龙隧道-北向南行驶

22.564871,114.017159

9

梅观公路南坪立交桥下北行-南-战略

LinearmodelPoly6:

f（x）=p1*x^6+p2*x^5+p3*x^4+p4*x^3+p5*x^2+

p6*x+p7

Coefficients（with95%confidencebounds）:

p1=-0.0001993（-0.00414,0.003742）

p2=-0.01499（-0.2879,0.2579）

p3=1.436（-5.746,8.618）

p4=-37.41（-126.7,51.85）

p5=397.5（-128.8,923.8）

p6=-1347（-2629,-64.28）

p7=1614（655.7,2572）

Goodnessoffit:

SSE:

3.985e+006

R-square:

0.8984

AdjustedR-square:

0.8626

RMSE:

484.2

22.587862,114.054716

10

梅观公路普滨加油站南行-北-战略

LinearmodelPoly6:

f（x）=p1*x^6+p2*x^5+p3*x^4+p4*x^3+p5*x^2+

p6*x+p7

Coefficients（with95%confidencebounds）:

p1=0.002506（-0.005123,0.01013）

p2=-0.2176（-0.7458,0.3107）

p3=7.375（-6.527,21.28）

p4=-122.8（-295.6,50）

p5=987.7（-31.23,2007）

p6=-2747（-5229,-264.2）

p7=2419（564.3,4274）

Goodnessoffit:

SSE:

1.493e+007

R-square:

0.8548

AdjustedR-square:

0.8036

RMSE:

937.3

22.597802,114.048826

11

清坪快速清水河联检站出口北行-南-战略

LinearmodelPoly6:

f（x）=p1*x^6+p2*x^5+p3*x^4+p4*x^3+p5*x^2+

p6*x+p7

Coefficients（with95%confidencebounds）:

p1=0.001115（-0.001455,0.003684）

p2=-0.08343（-0.2614,0.0945）

p3=2.392（-2.291,7.075）

p4=-34.05（-92.25,24.14）

p5=251.2（-91.96,594.4）

p6=-697.2（-1533,139）

p7=732.4（107.7,1357）

Goodnessoffit:

SSE:

1.694e+006

R-square:

0.8922

AdjustedR-square:

0.8541

RMSE:

315.7

22.618156,114.09556

12

清坪快速清水河联检站入口南行-北-战略

LinearmodelPoly6:

f（x）=p1*x^6+p2*x^5+p3*x^4+p4*x^3+p5*x^2+

p6*x+p7

Coefficients（with95%confidencebounds）:

p1=5.485e-005（-0.0008694,0.0009791）

p2=-0.002064（-0.06607,0.06194）

p3=0.04505（-1.639,1.729）

p4=-1.98（-22.91,18.95）

p5=37.81（-85.63,161.3）

p6=-145.2（-445.9,155.6）

p7=197.8（-26.86,422.5）

Goodnessoffit:

SSE:

2.192e+005

R-square:

0.9468

AdjustedR-square:

0.928

RMSE:

113.6

22.615467,114.096193

13

保洁路清水河检查站出-南-战略

LinearmodelPoly6:

f（x）=p1*x^6+p2*x^5+p3*x^4+p4*x^3+p5*x^2+

p6*x+p7

Coefficients（with95%confidencebounds）:

p1=0.000111（-0.001049,0.001271）

p2=-0.01558（-0.09592,0.06476）

p3=0.6547（-1.459,2.769）

p4=-12.35（-38.62,13.93）

p5=111.6（-43.3,266.6）

p6=-358.6（-736.1,18.91）

p7=446.4（164.4,728.4）

Goodnessoffit:

SSE:

3.454e+005

R-square:

0.9123

AdjustedR-square:

0.8813

RMSE:

142.5

22.588758,114.112716

14

西环路清水河检查站入-北-战略

LinearmodelPoly6:

f（x）=p1*x^6+p2*x^5+p3*x^4+p4*x^3+p5*x^2+

p6*x+p7

Coefficients（with95%confidencebounds）:

p1=0.0001109（-0.0002573,0.0004792）

p2=-0.01031（-0.03581,0.01519）

p3=0.3734（-0.2977,1.045）

p4=-6.663（-15,1.677）

p5=57.71（8.528,106.9）

p6=-175.9（-295.7,-56.06）

p7=224.5（135,314.1）

Goodnessoffit:

SSE:

3.48e+004

R-square:

0.9117

AdjustedR-square:

0.8805

RMSE:

45.25

22.589449,114.112702

15

布吉路-深惠路南向北行驶

22.582337,114.117852

16

深惠路-布吉路北向南行驶

22.589878,114.114349

17

丹沙路沙湾检查站入-北-战略

LinearmodelPoly6:

f（x）=p1*x^6+p2*x^5+p3*x^4+p4*x^3+p5*x^2+

p6*x+p7

Coefficients（with95%confidencebounds）:

p1=0.0005322（-0.0005447,0.001609）

p2=-0.03997（-0.1145,0.0346）

p3=1.168（-0.7945,3.131）

p4=-17（-41.38,7.393）

p5=126.4（-17.45,270.2）

p6=-368.6（-719.1,-18.22）

p7=618.1（356.3,879.9）

Goodnessoffit:

SSE:

2.976e+005

R-square:

0.8272

AdjustedR-square:

0.7662

RMSE:

132.3

22.603579,114.165255

18

沙湾路沙湾检查站出-南-战略

LinearmodelPoly6:

f（x）=p1*x^6+p2*x^5+p3*x^4+p4*x^3+p5*x^2+

p6*x+p7

Coefficients（with95%confidencebounds）:

p1=0.0003054（-0.0001421,0.000753）

p2=-0.02173（-0.05272,0.009258）

p3=0.5829（-0.2327,1.398）

p4=-7.476（-17.61,2.659）

p5=47.56（-12.21,107.3）

p6=-113.4（-259,32.24）

p7=221.5（112.7,330.3）

Goodnessoffit:

SSE:

5.14e+004

R-square:

0.8677

AdjustedR-square:

0.8209

RMSE:

54.99

22.60635,114.16387

数据为空、为0、为红字的属于设备故障，仅供参考。

日期栏以不同颜色填充区分不同天

布吉关、福龙隧道无批量数据，抽样数据见表2

可以简单的思考问题，当进入交叉口的车辆数大于驶出交叉口的车辆数时，道路在交叉口处就会发生拥堵现象，当然这是一种简化了的思考方法，说明道路在交叉口的设计通行能力不足，或者交叉口的设计不合理。

我们以高峰时段为例，通过理论计算来分析驶入交叉口和驶出交叉口的车辆数，发现在高峰时段（主要是下午5点至7点）梅林关立交出现了明显的拥堵情况。

下面我们来分析造成交通拥堵的原因，并给出相应的措施。

（一）机动车快速增长引发的经常性、大面积交通拥堵

　　深圳市的机动车保有量急剧增长，车辆使用率居高不下，交通量持续攀升。

截至2010年底，全市道路总里程已经超过6000公里，车辆保有量达170万辆，加上长期在深行驶的港澳车及外地车辆，机动车总量已经接近200万辆，车辆密度已达324辆/公里，成为中国车辆密度最高的城市。

车辆的快速增加与有限的道路空间的矛盾进一步加剧，交通拥堵问题也越来越严重。

　　对策：

　　由于汽车行业仍是国家的支柱产业，在现阶段，仍不宜抑制汽车行业的发展，但是，我们可以通过以下手段，抑制小汽车的过度使用。

（1）通过经济杠杆调整，加大出行成本，提高拥车成本

部分国人存在驾驶小汽车是一种身份象征的心里，在很多不必要使用汽车出行的时候，如附近市场买菜、喝下午茶还要开车，因此可以考虑使用中心区高峰时段拥堵收费以及高额停车收费策略，抑制私人小汽车的过度使用，用经济杠杆调节需求与供给，缓解道路交通拥堵。

同时，配套的要优先发展公共交通，特别是要注意配套中心区外围地铁换乘站周边的停车设施建设。

随着汽车工业的发展，目前拥有多辆小汽车对于城市很多家庭来讲不是难事，这也导致了汽车保有量的增加。

因此，建议通过开征车牌号税、控制车牌供给以及以家庭为单位对第二部、第三部小汽车开征高额税，提高拥车成本，控制小汽车的供给。

我们可以通过下面的供求曲线来限制小汽车的使用。

社会对小汽车的需求量可以用曲线来表示。

当小汽车的价格和其相关的使用费用增长时，社会对小汽车的需求量会下降，反之，当小汽车的价格下跌时，社会对它的需求量会增长。

这样的关系在函数关系上是单调递减的，其图像是一下降的曲线，如图所示的曲线

和

设P=P（Q）是需求曲线方程。

令

e=-

=-

e

我们可以通过上述曲线来制定相应的政策。

若e等于2.5，它的需求量就会下降2.5%。

因此我们可以通过道路的允许通行量，调整小汽车的价格，达到解决交通拥堵问题的目的。

额下降的曲线市用曲