 4平行四边形三角形的面积.docx
4平行四边形三角形的面积.docx
- 文档编号:5126574
- 上传时间:2022-12-13
- 格式:DOCX
- 页数:16
- 大小:225.01KB
4平行四边形三角形的面积.docx
《4平行四边形三角形的面积.docx》由会员分享,可在线阅读,更多相关《4平行四边形三角形的面积.docx(16页珍藏版)》请在冰豆网上搜索。
4平行四边形三角形的面积
学科教师辅导讲义
学生姓名:
年级:
5课时数:
3
辅导科目:
数学辅导教师:
辅导内容:
平行四边形、三角形的面积辅导日期:
教学目标:
1.了解平行四边形与长方形面积的关系,
2.了解三角形与平行四边形面积的关系。
3.熟练掌握平行四边形与三角形的面积公式。
【课前知识点回顾】
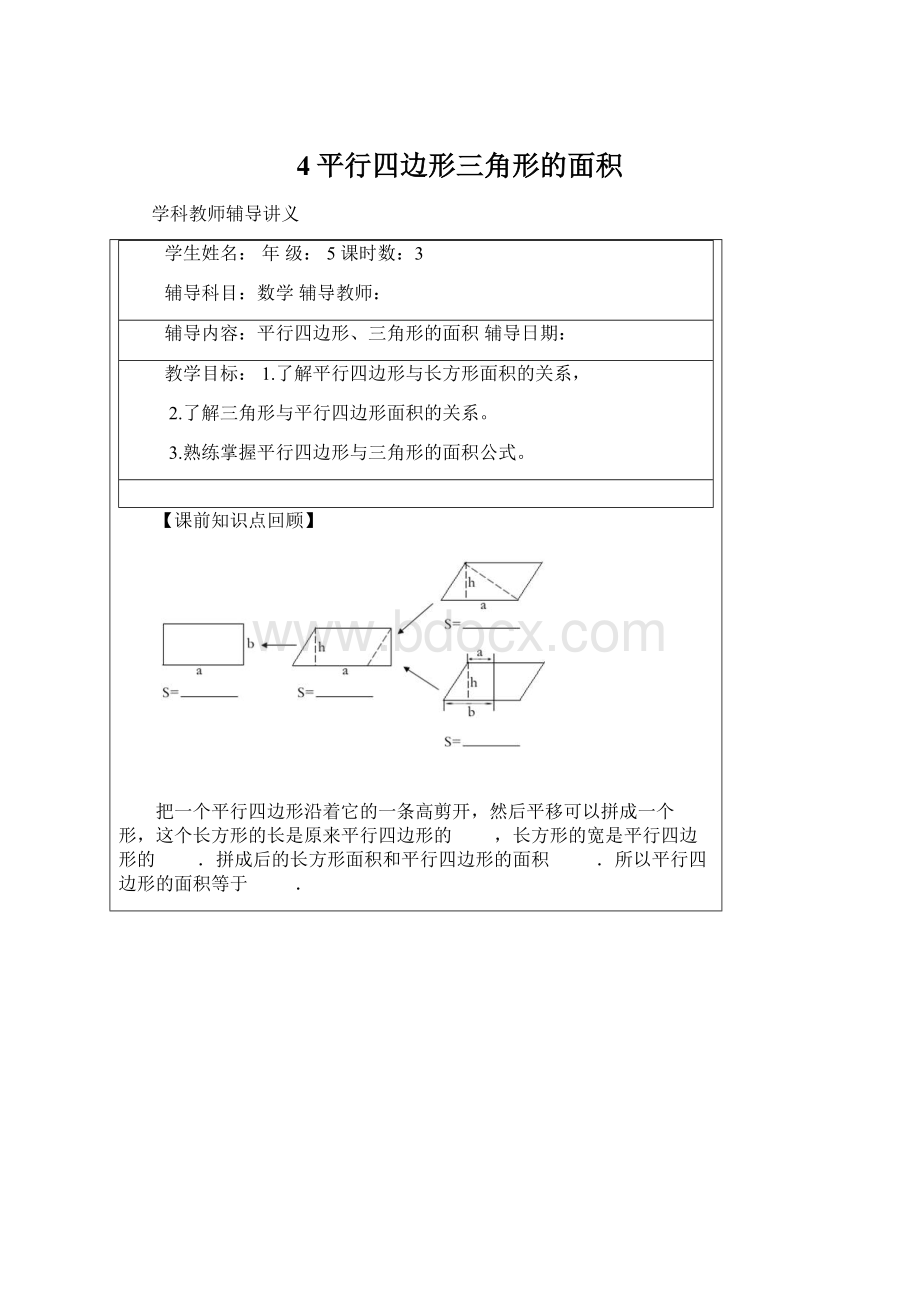
把一个平行四边形沿着它的一条高剪开,然后平移可以拼成一个 形,这个长方形的长是原来平行四边形的 ,长方形的宽是平行四边形的 .拼成后的长方形面积和平行四边形的面积 .所以平行四边形的面积等于 .
【同步知识讲解】
知识点1:
平行四边形的面积
题型一:
平行四边形与长方形面积的关系
例1:
把一个长方形框架拉“斜”成一个平行四边形,这个平行四边形和原长方形比( )
A.周长一样B.面积一样C.周长和面积都一样D.不能确定
【分析】把一个长方形的框架拉成一个平行四边形后,四条边的长度没变,也就是它们的和没有发生变化,即它的周长不变,高变短了,所以面积变小了,据此解答即可.
变式:
1.一个用四根木条钉成的长方形框架,用手拉成平行四边形,这个平行四边形和原来长方形比较( )
A.面积变大B.面积变小C.面积不变D.没有数据,不能判断
【分析】一个用四根木条钉成的长方形框架,用手拉成平行四边形,周长不变,面积变小.因为在直角三角形中,直角边小于斜边,也就是拉成平行四边形的高小于长方形的宽.据此解答.
2.将一个能活动的平行四边形拉成长方形,其面积( )
A.变大B.变小C.不变
【分析】把一个平行四边形木框拉成长方形后,平行四边形的底就变成长方形的长,底的邻边就变成长方形的宽,所以高变长了,则面积就变大了.
.
3.用四根细木条钉成一个长方形框,将它拉成平行四边形.以下说法正确的是( )
A.周长变了,面积不变B.周长不变,面积变了
C.周长和面积都变了D.周长和面积都不变
【分析】把一个木条钉成的长方形框拉成一个平行四边形后,每条边的长度都不变,所以周长不变,但是高变短了,于是由平行四边形和长方形的面积公式可知,它的面积变小了,据此解答即可.
题型二:
计算平行四边形的面积
例1:
有一块平行四边形形状的菜地,底边长30米,这条底边上的高长14米,那么这块菜地的面积是 平方米.
【分析】根据平行四边形的面积公式:
S=ah,把数据代入公式解答.
变式:
1.一个平行四边形的底是12.5cm,高是2.4cm,它的面积是 .
【分析】根据平行四边形的面积=底×高,代入数据即可解答.
2.有一块形如平行四边形的白菜地,它的底为36米,高为15米,如果每棵白菜占地9分米2,这块地能栽 棵白菜.
【分析】首先根据平行四边形的面积公式:
S=ah,求出这块菜地的面积,然后用菜地的面积除以每棵白菜的占地面积即可.
3.一块平行四边形菜地,底是32分米,高是15分米.如果每平方米能收8千克青菜.这块菜地一共可以收 千克青菜.
【分析】首先根据平行四边形的面积公式:
S=ah,求出菜地的面积,然后根据单产量×数量=总产量,据此列式解答.
4.在一个底为40米,高为50米的平行四边形地里种上柚子树,每棵柚子树占地20平方米.这块地里一共能种 棵柚子树.
【分析】首先根据平行四边形的面积公式:
S=ah,求出这块地的面积,然后用这块地的面积除以每棵树的占地面积即可.
题型三:
通过面积求高或底
例1:
一个平行四边形的面积是27平方厘米,底边上的高是3cm,它的底是 厘米.
【分析】根据平行四边形的面积公式:
S=ah,那么a=S÷h,把数据代入公式解答.
变式:
1.一个平行四边形的面积是60平方米,已知它的高是3米,底是 米.
【分析】根据平行四边形的面积公式:
S=ah,那么a=S÷h,把数据代入公式解答.
2.一个平行四边形的面积是75m2,它的底是15m,对应的高是 m.
【分析】根据平行四边形的面积公式:
S=ah,那么h=S÷a,把数据代入公式解答.
3.如图,平行四边形的周长是 分米.
【分析】根据平行四边形的面积公式S=ah,用底12乘高10求出平行四边形的面积,再用平行四边形的面积除以另一个高8求出这个高对应的底,然后把平行四边形的四条边相加就是平行四边形的周长.
知识点2:
三角形的面积
题型一:
三角形的周长
例1:
一个等边三角形的周长是18厘米,它的一条边的长度是 .
【分析】因为等边三角形的三条边都相等,求边长,用“等边三角形的周长÷3”进行解答即可.
变式:
1.一块等腰三角形菜地,其中两条边的长分别是5米和10米.如果给这块菜地围上篱笆,篱笆长 米.
【分析】根据任意两边之和大于第三边,可知等腰三角形的腰的长度是10米,底边长5米,据此解答即可.
2.等腰三角形的两条边长分别是3cm和6cm,则它的周长是 .
【分析】根据三角形的三条边的关系,这个等腰三角形的腰是6厘米,底是3厘米,把三角形的三条边的数据相加即可解答.
3.用一根30cm的铁丝围一个等腰三角形.如果底边长是8cm,那么一条腰长 cm;如果一边长是7厘米,那么另两条边分别是 cm, cm.
【分析】
(1)由题意可知,等腰三角形的周长是30厘米,用周长减去底边的长度再除以2就是等腰三角形的腰长;
(2)因为等腰三角形的两条腰是相等的,而当7厘米是等腰三角形的腰时,此时底边是30﹣7﹣7=16厘米,而7+7<16,所以此种情况不存在;所以应是底边是7厘米,此时腰是(30﹣7)÷2=11.5厘米,据此解答.
题型二:
三角形与平行四边形面积的关系
例1:
一个三角形的面积是6.9平方厘米,与它等底等高的平行四边形的面积是 .
【分析】因为平行四边形的面积等于与它等底等高的三角形的面积的2倍,所以用三角形的面积乘2就是平行四边形的面积.
例题2:
一个三角形的面积是4.8m2,高是3m,与它面积相等高也相等的平行四边形的底是( )m.
A.1.6B.0.8C.3.2D.4.8
【分析】根据平行四边形的面积公式S=ah,得出a=S÷h,把平行四边形的面积4.8m2,高是3m代入关系式求出底.
变式:
1.一个三角形的面积是4平方厘米,与它等底等高的平行四边形的面积是 平方厘米.
【分析】等底等高的平行四边形的面积是三角形面积的2倍,根据求一个数的几倍是多少,用乘法解答.
2.如图,阴影部分的面积是32.5dm2,那么平行四边形的面积是 dm2.
【分析】因为等底等高的平行四边形的面积是三角形面积的2倍,所以用三角形的面积乘2即可求出平行四边形的面积.
3.如图是一个平行四边形,它包含了三个三角形,其中两个白三角形的面积15平方厘米和25平方厘米,中间涂色的三角形面积是 平方厘米.
【分析】由题意可知:
涂色部分的面积和空白部分的面积相等,都等于平行四边形的面积的一半,据此解答即可.
4.图中阴影的面积是12平方厘米,平行四边形的高是 厘米.
【分析】根据观察图形可知:
阴影部分三角形与平行四边形等底等高,等底等高的平行四边形的面积是三角形面积的2倍,根据求一个数的几倍是多少,用乘法求出平行四边形的面积,再根据平行四边形的面积公式:
S=ah,那么h=S÷a,把数据代入公式解答.
题型三:
三角形的面积计算
例1:
一个三角形的苗圃,底边长200米,高约160米.这个苗圃的面积大约是 平方米?
【分析】利用三角形的面积=底×高÷2,即可求出这个三角形的面积即可.
变式:
1.一块三角形铁皮,底是5分米,高是40厘米,这块铁皮的面积是 平方厘米.
【分析】三角形的面积公式是:
三角形的面积=底×高÷2,将数据代入公式即可求得结果.
2.三角形的底是4.2分米,高是3分米,面积是 .
【分析】根据三角形的面积公式:
三角形面积=底×高÷2,直接列式求解即可.
3.有一种三角形锦旗的底是25厘米,高是30厘米.做16面这样的锦旗至少需要 平方厘米的红丝绸.
【分析】先根据三角形面积=底×高÷2,求出制作一面锦旗需要红丝绸多少平方厘米,再乘16即可求解.
题型四:
根据面积计算三角形的底或高
例1:
三角形的面积是18平方厘米,底边长是6厘米,它的底边上的高是 厘米
【分析】根据三角形的面积公式:
S=ah÷2,那么h=2S÷a,把数据代入公式解答即可.
变式:
1.一个三角形的面积是30cm2,底是5cm,它的高是 .
【分析】根据三角形的面积=底×高÷2可知,要求三角形的高,先用三角形的面积乘上2,再除以它的底即可.
2.一个三角形的面积是16cm2,其中一个底是8cm,这个底上的高是 cm,用两个这样的三角形拼成的平行四边形的面积是 cm2.
【分析】三角形的面积=底×高÷2,所以三角形的高=三角形的面积×2÷底,由此代入求出这个三角形的高;用两个这样的三角形拼成的平行四边形的面积就是一个三角形面积的2倍,用三角形的面积乘2即可求解.
3.一个三角形的面积是200平方米,高是20米,底是 米,与它等底等高的平行四边形面积
是 平方米.
【分析】
(1)根据三角形的面积公式S=ah÷2,可知面积×2÷高=底,代入数值解答即可;
(2)根据等底等高的平行四边形的面积是三角形的面积的2倍,用三角形的面积乘2就是平行四边形的面积.
4.一块三角形草坪面积是96平方米,底是16米,高是 米.
【分析】根据三角形的面积公式可知,三角形的高=面积×2÷底,由此代入数据计算即可求解.
5.一个三角形的底是6cm,高是5cm,它的面积是 cm2,与它等底等高的平行四边形的面积是
cm2.
【分析】根据三角形的面积=底×高÷2,和平行四边形的面积=底×高,直接计算即可.
知识点三:
计算面积
例1:
计算下面图形的面积.(单位:
cm)
【分析】根据平行四边形的面积公式:
S=ah,把数据代入公式解答即可.
变式:
1.看图计算面积(单位:
dm)
【分析】根据平行四边形的面积公式:
S=ah,把数据代入公式解答.
2.计算下面图形的面积(单位:
dm)
【分析】根据平行四边形面积=底×高,找准底是10,高是9,代入公式计算.
3.计算如图的面积.
【分析】根据平行四边形的面积=底×高求解即可.
4.求平行四边形中长是10米的底边上的高.
【分析】根据平行四边形的面积=底×高,求出平行四边形的面积,再根据平行四边形的高=面积÷底,列出算式计算即可求解.
例2:
计算下面三角形的面积.
(1)
(2)
【分析】根据三角形面积=底×高÷2,代入数据解答即可.
变式:
1.乙三角形的面积比甲三角形的面积大多少平方厘米?
【分析】由图意可知:
乙三角形的面积比甲三角形面积大的面积也就是乙加上空白部分与甲加上空白部分的差,根据三角形的面积公式求出甲加上空白部分的面积和乙加上空白部分的面积,从而可以求出甲与乙的面积差.
2.求下列各三角形的面积.
【分析】三个三角形的都告诉了底和高,根据三角形面积计算公式“S=ah÷2”即可分别求出各三角形的面积.各图中有有用条件和干扰条件.
(1)25、12是有用条件,13是干扰条件;
(2)35、8是有用条件,10是干扰条件;(3)10、18是有用条件,28是干扰条件.
3.如图,求图示三角形的面积.(单位:
cm)
【分析】三角形的底和高已知,依据三角形的面积S=
ah,代入数据即可求解.
4.计算下列图形的面积:
(单位:
厘米)
【分析】根据三角形的面积公式S=ah÷2进行解答即可.
【课堂同步知识训练】
1.一种三角巾的形状是等腰直角三角形,直角边长8分米.现有一块长4米,宽16分米的长方形白布,用它最多可以剪出 块这样的三角巾.
2.计算下面这块地的面积是 .(单位:
米)
3.一个平行四边形框架相邻两条边的长分别是5cm和10cm.它的一条高是6cm,它的面积是 cm2;沿对角拉成长方形后的周长是 cm.
4.一块平行四边形绿地底是30米,高是底的1.5倍,这块绿地的面积是 平方米.
5.如图,阴影三角形的面积是69平方厘米,平行四边形的面积是 平方厘米.
【知识能力训练】
1.一个平行四边形的面积为15平方厘米,底扩大3倍,高扩大2倍,这时平行四边形的面积是 平方厘米.
【解答】解:
15×(3×2)
=15×6
=90(平方厘米),
答:
这时平行四边形的面积是90平方厘米.
故答案为:
90.
2.平行四边的面积是15m2,将它的高扩大到原来的3倍,底不变,这时平行四边形的面积是 m2.
【解答】解:
15×3=45(平方厘米)
答:
面这时平行四边形的面积是45m2.
故答案为:
45.
3.甲乙两个三角形的面积相等,如果甲三角形的底是乙三角形底的二分之一,那么乙三角形的高就是甲三角形高的______.
【解答】解:
设甲的底是a,高是b,
S△甲=ab÷2
S△乙=2a×高÷2
又因S△甲=S△乙
则2a×高÷2=ab÷2
即2a高=ab
高=
b
所以乙三角形的高就是甲三角形高的
.
故答案为:
.
4.把一个三角形放大三倍,原来三角形的底是5厘米,高是4厘米,放大后的底是 厘米,高是_____ 厘米.面积是 平方厘米.
【解答】解:
5×3=15(厘米)
4×3=12(厘米)
×15×12=90(平方厘米)
答:
放大后的底是15厘米,高是12厘米,面积是90平方厘米.
故答案为:
15,12,90.
【课后知识应用】
1.一块平行四边形地的底为100米,高为24米,按照每株占地2平方分米的标准种大豆.如果每株收大豆0.5千克,这块地大约可收大豆多少千克?
2.一块平行四边形菜地的高是26m,底是高的3倍.这块菜地的面积是多少平方米?
3.一块长方形的萝卜地,长4米,宽2米,王大爷在这块地里一共收萝卜120千克,平均每平方米收萝卜多少千克?
4.一块平行四边形的菜地,它的底是24米,高是5米,共收蔬菜360千克,这块地平均每平方米收蔬菜多少千克?
5.一块平行四边形的菜地,底是30米,是高的2倍,每棵白菜大约需要6平方分米,这块白菜地一共可以种多少棵白菜?
6.一块三角形菜地的面积是80平方米,高是20米.这块三角形菜地的底是多少米?
7.王叔叔家有一个正方形鱼塘,周长32m,这个鱼塘的面积是多少平方米?
8.买一块底是14m、高是8m的三角形钢板用去672元,这种钢板平均每平方米多少元?
9.编织小组要编织一批底和高都是0.6米的三角形头巾.编织这样的头巾每平方米需绒线0.7千克,编织100条头巾需用绒线多少千克?
10.运动会就要开始了,老师要求每位同学都准备一面底是30cm,高是10cm的三角形小红旗,全班42名同学共需要多少cm2的红纸?
(不计余料)
答案:
1.解:
2平方分米=0.02平方米
100×24÷0.02×0.5
=2400÷0.02×0.5
=120000×0.5
=60000(千克)
答:
这块地大约可收大豆60000千克.
2.解:
(26×3)×26
=78×26
=2028(平方米)
答:
这块菜地的面积是2028平方米.
3.解:
120÷(5×2)
=120÷10
=12(千克)
答:
平均每平方米收萝卜12千克.
4.解:
360÷(24×5)
=360÷120
=3(千克)
答:
这块地平均每平方米收蔬菜3千克.
5.解:
6平方分米=0.06平方米,
30×(30÷2)÷0.06
=30×15÷0.06
=450÷0.06
=7500(棵)
答:
这块白菜地一共可以种7500棵白菜.
6.解:
80×2÷20
=160÷20
=8(米)
答:
这块三角形菜地的底是8米.
7.解:
32÷4=8(米)
8×8=64(平方米)
答:
鱼塘面积是64平方米.
8.解:
672÷(14×8÷2)
=672÷56
=12(元)
答:
这种钢板平均每平方米12元.
9.解:
0.6×0.6÷2×100×0.7
=0.18×100×0.7
=18×0.7
=12.6(千克)
答:
编织100条头巾需用绒线12.6千克.
10.解:
30×10÷2×42
=150×42
=6300(平方厘米)
答:
全班42名同学共需要6300平方厘米的红纸.(不计余料)
审核人:
尹王冠
- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 平行四边形 三角形 面积
 冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。


 广东省普通高中学业水平考试数学科考试大纲Word文档下载推荐.docx
广东省普通高中学业水平考试数学科考试大纲Word文档下载推荐.docx
