四边形知识点经典总结材料.docx

四边形知识点经典总结材料.docx

《四边形知识点经典总结材料.docx》由会员分享，可在线阅读，更多相关《四边形知识点经典总结材料.docx（15页珍藏版）》请在冰豆网上搜索。

四边形知识点经典总结材料

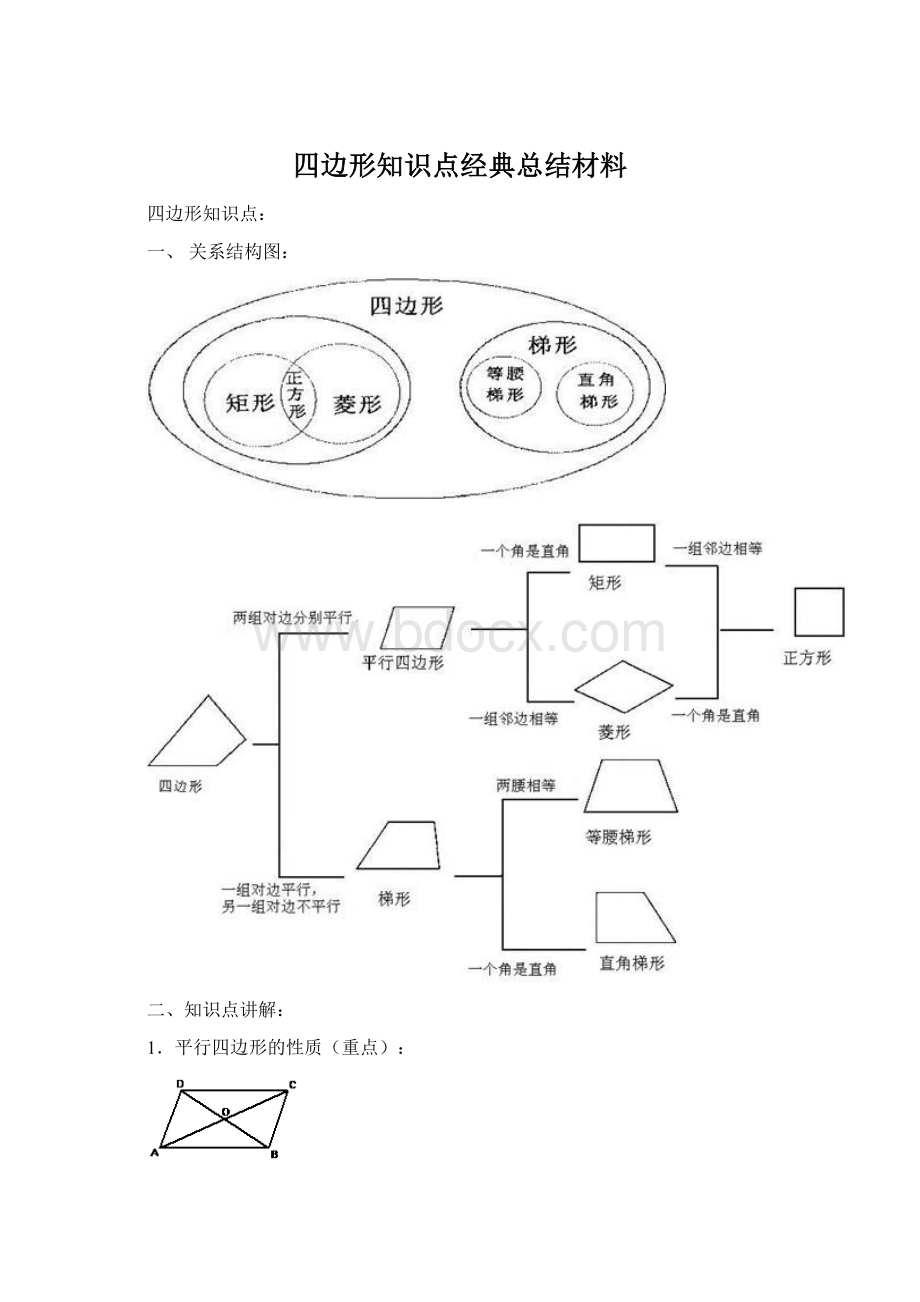
四边形知识点：

一、关系结构图：

二、知识点讲解：

1．平行四边形的性质（重点）：

ABCD是平行四边形

2.平行四边形的判定（难点）：

.

3.矩形的性质：

因为ABCD是矩形

（4）是轴对称图形，它有两条对称轴．

4矩形的判定：

矩形的判定方法：

（1）有一个角是直角的平行四边形；

（2）有三个角是直角的四边形；

　　　　　　　　　　（3）对角线相等的平行四边形；

　　　　　　　　　　（4）对角线相等且互相平分的四边形．四边形ABCD是矩形.

5.菱形的性质：

因为ABCD是菱形

6.菱形的判定：

四边形四边形ABCD是菱形.

7.正方形的性质：

ABCD是正方形

8.正方形的判定：

四边形ABCD是正方形.

名称

定义

性质

判定

面积

平

行

四

边

形

两组对边分别平行的四边形叫做平行四边形。

1对边平行；

②对边相等；

③对角相等；

④邻角互补；

⑤对角线互相平分；

⑥是中心对称图形

①定义；

②两组对边分别相等的四边形；

③一组对边平行且相等的四边形；

④两组对角分别相等的四边形；

⑤对角线互相平分的四边形。

S=ah（a为一边长，h为这条边上的高）

矩

形

有一个角是直角的平行四边形叫做矩形

除具有平行四边形的性质外，还有：

①四个角都是直角；②对角线相等；③既是中心对称图形又是轴对称图形。

①有三个角是直角的四边形是矩形；②对角线相等的平行四边形是矩形；③定义。

S=ab（a为一边长，b为另一边长）

菱

形

有一组邻边相等的平行四边形叫做菱形。

除具有平行四边形的性质外，还有①四边形相等；②对角线互相垂直，且每一条对角线平分一组对角；③既是中心对称图形又是轴对称图形。

①四条边相等的四边形是菱形；②对角线垂直的平行四边形是菱形；③定义。

①S=ah（a为一边长，h为这条边上的高）；

②

（b、c为两条对角线的长）

正

方

形

有一组邻边相等且有一个角是直角的平行四边形叫做正方形

具有平行四边形、矩形、菱形的性质：

①四个角是直角，四条边相等；②对角线相等，互相垂直平分，每一条对角线平分一组对角；③既是中心对称图形又是轴对称图形。

①有一组邻边相等的矩形是正方形；②有一个角是直角的菱形是正方形；③定义。

①

（a为边长）；

②

（b为对角线长）

三．精典例题解答：

1．已知：

如图，E、F是平行四边形ABCD的对角线AC上的两点，AE=CF。

　　　　　　求证：

（1）△ADF≌△CBE；

（2）EB∥DF。

　　证明：

（1）∵AE=CF∴AE+EF=CF+FE即AF=CE

　　　　　　　又ABCD是平行四边形，∴AD=CB，AD∥BC∴∠DAF=∠BCE

　　　　　　　在△ADF与△CBE中

∴△ADF≌△CBE（SAS）

（2）∵△ADF≌△CBE∴∠DFA=∠BEC∴DF∥EB

　　例1图例2图

2．如图，平行四边形ABCD的对角线AC、BD相交于点O，E、F是直线AC上的两点，并且AE=CF，求证：

四边形BFDE是平行四边形。

　　　　证明：

∵四边形ABCD是平行四边形

　　　　　∴OA=OC，OB=OD

　　　　　又∵AE=CF

　　　　　∴OA+AE=OC+CF即OE=OF

　　　　　∴四边形BFDE是平行四边形

3．如图，在梯形纸片ABCD中，AD∥BC，AD>CD，将纸片沿过点D的直线折叠，使点C落在AD上的点C’处，折痕DE交BC于点E，连结

。

　　求证：

四边形

是菱形。

　　　　证明：

根据题意可知

　　　　　则

，

，

　　　　　∵AD∥BC∴

∴∠CDE=∠CED

　　　　　∴CD=CE∴

∴四边形

为菱形

　例3图

4．把正方形ABCD绕着点A，按顺时针方向旋转得到正方形AEFG，边FG与BC交于点H（如图）。

试问线段HG与线段HB相等吗？

请先观察猜想，然后再证明你的猜想。

　　解：

HG=HB。

　　　　证法1：

连结AH，

　　　　　　　∵四边形ABCD，AEFG都是正方形

　　　　　　　∴∠B=∠G=90°

　　　　　　　由题意知AG=AB，又AH=AH

　　　　　　　∴Rt△AGH≌Rt△ABH（HL）

　　　　　　　∴HG=HB

　　　　证法2：

连结GB

　　　　　　　∵四边形ABCD，AEFG都是正方形

　　　　　　　∴∠ABC=∠AGF=90°

　　　　　　　由题意知AB=AG

　　　　　　　∴∠AGB=∠ABG

　　　　　　　∴∠ABC-∠ABG=∠AGF-∠AGB即∠HBG=∠HGB

　　　　　　　∴HG=HB

5．如图，正方形ABCD绕点A逆时针旋转n°后得到正方形AEFG，边EF与CD交于点O。

（1）以图中已标有字母的点为端点连结两条线段（正方形的对角线除外），要求所连结的两条线段相

　　　　交且互相垂直，交说明这两条线段互相垂直的理由；

（2）若正方形的边长为2cm，重叠部分（四边形AEOD）的面积为

，求旋转的角度n。

　　　　解：

（1）我连结的两条相交且互相垂直的线段是____AO____和____DE____。

　　　　　　理由如下：

　　　　　　∵在Rt△ADO与Rt△AEO中，AD=AE，AO=AO，

　　　　　　∴Rt△ADO≌Rt△AEO

　　　　　　∴∠DAO=∠OAE（即AO平分∠DAE）

　　　　　　∴AO⊥DE（等腰三角形的三线合一）

　　　　　　注：

其它的结论也成立如GD⊥BE。

（2）∵四边形AEOD的面积为

　　　　　　∴三角形ADO的面积=

　　　　　　∵AD=2

　　　　　　∴

　　　　　　∴∠DAO=30°

　　　　　　∴∠EAB=30°即旋转的角度是30°

　例5图例6图

6．四边形ABCD、DEFG都是正方形，连接AE、CG。

（1）求证：

AE=CG；

（2）观察图形，猜想AE与CG之间的位置关系，并证明你的猜想。

证明：

（1）如图，

　　　　　　　∵AD=CD，DE=DG，∠ADC=∠GDE=90°

　　　　　　　又∠CDG=90°+∠ADG=∠ADE

　　　　　　　∴△ADE≌△CDG

　　　　　　　∴AE=CG

（2）猜想：

AE⊥CG。

　　　　　　　证明：

如图，设AE与CG交点为M，AD与CG交点为N

　　　　　　　　　　∵△ADE≌△CDG

　　　　　　　　　　∴∠DAE=∠DCG

　　　　　　　　　　又∵∠ANM=∠CND

　　　　　　　　　　∴△AMN∽△CDN

　　　　　　　　　　∴∠AMN=∠ADC=90°

　　　　　　　　　　∴AE⊥CG

7．已知：

如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E，

（1）求证：

四边形ADCE为矩形；

（2）当△ABC满足什么条件时，四边形ADCE是一个正方形？

并给出证明。

　　　证明：

（1）在△ABC中，AB=AC，AD⊥BC

　　　　　　　∴∠BAD=∠DAC

　　　　　　　∵AN是△ABC外角∠CAM的平分线

　　　　　　　∴∠MAE=∠CAE

　　　　　　　∴

　　　　　　　又∵AD⊥BC，CE⊥AN

　　　　　　　∴∠ADC=∠CEA=90°

　　　　　　　∴四边形ADCE为矩形

（2）当

时（答案不唯一），四边形ADCE是正方形。

　　　　　　　证明：

∵AB=AC，AD⊥BC于D

　　　　　　　　　　∴

　　　　　　　　　　又

　　　　　　　　　　∴DC=AD

　　　　　　　　　　由

（1）四边形ADCE为矩形

　　　　　　　　　　∴矩形ADCE是正方形

　　例8图

8．将平行四边形纸片ABCD按如图方式折叠，使点C与A重合，点D落到

处，折痕为EF。

（1）求证：

△ABE≌△AD′F；

（2）连接CF，判断四边形AECF是什么特殊四边形？

证明你的结论。

　　证明：

（1）由折叠可知：

，

，

　　　　　　　∵四边形ABCD是平行四边形

　　　　　　　∴∠B=∠D，AB=CD，∠C=∠BAD

　　　　　　　∴∠B=∠D′，AB=AD′

　　　　　　　∠D′AE=∠BAD，即∠1+∠2=∠2+∠3

　　　　　　　∴∠1=∠3

　　　　　　　∴△ABE≌△AD′F

（2）四边形AECF是菱形。

　　　　　　　由折叠可知：

AE=EC，∠4=∠5

　　　　　　　∵四边形ABCD是平行四边形

　　　　　　　∴AD∥BC

　　　　　　　∴∠5=∠6

　　　　　　　∴∠4=∠6

　　　　　　　∴AF=AE

　　　　　　　∵AE=EC

　　　　　　　∴AF=EC

　　　　　　　又∵AF∥EC

　　　　　　　∴四边形AECF是平行四边形

　　　　　　　∵AF=AE∴四边形AECF是菱形。

9．如下图，已知P正方形ABCD的对角线AC上一点（不与A、C重合），PE⊥BC于点E，PF⊥CD于点F．

（1）求证：

BP=DP；

（2）若四边形PECF绕点C按逆时针方向旋转，在旋转过程中是否总有BP=DP？

若是，请给予证明；若不

　　　　是，请用反例加以说明；

　　（3）试选取正方形ABCD的两个顶点，分别与四边形PECF的两个顶点连结，使得到的两条线段在四边

　　　　形PECF绕点C按逆时针方向旋转的过程中长度始终相等，并证明你的结论．

　　思路分析：

（1）解法一：

在△ABP与△ADP中，利用全等可得BP=DP．

　　　　　　　　　解法二：

利用正方形的轴对称性，可得BP=DP．

（2）不是总成立．当四边形PECF绕点C按逆时针方向旋转，点P旋转到BC边上时，

　　　　　　　　　DP>DC>BP，此时BP=DP不成立．

　　　　　　　　　说明：

未用举反例的方法说理的不得分．

　　　　　　　（3）连接BE、DF，则BE与DF始终相等．

　　　　　　　　　在图中，可证四边形PECF为正方形，

　　　　　　　　　在△BEC与△DFC中，可证△BEC≌△DFC．

　　　　　　　　　从而有BE=DF

10．为创建绿色校园，学校决定对一块正方形的空地进行种植花草，现向学生征集设计图案．图案要求只能用圆弧在正方形内加以设计，使正方形和所画的图弧构成的图案，既是轴对称图形又是中心对称图形．种植花草部分用阴影表示．请你在图③、图④、图⑤中画出三种不同的的设计图案．

　　提示：

在两个图案中，只有半径变化而圆心不变的图案属于同一种，例如：

图①、图②只能算一种．

　　解：

以下为不同情形下的部分正确画法，答案不唯一．

11．如图，等腰梯形ABCD中，AB=15，AD=20，∠C=30°。

点M、N同时以相同速度分别从点A、点D开始在AB、AD（包括端点）上运动。

（1）设ND的长为x，用x表示出点N到AB的距离，并写出x的取值范围。

（2）设

，用t表示△AMN的面积。

　　（3）求△AMN的面积的最大值，并判断取最大值时△AMN的形状。

　　解：

（1）过点N作BA的垂线NP，交BA的延长线于点P。

　　　　　　由已知：

，

。

　　　　　　∵四边形ABCD是等腰梯形，AB∥CD，∠D=∠C=30°，

　　　　　　∴∠PAN=∠D=30°。

　　　　　　在Rt△APN中，

，

　　　　　　即点N到AB的距离为

。

　　　　　　∵点N在AD上，

，点M在AB上，

，

　　　　　　∴x的取值范围是

。

（2）根据

（1），

。

　　　　（3）∵

，∴当t=0时，即x=10时，

有最大值25。

　　　　　　当x=10时，即ND=AM=10，AN=AD-ND=10，即AM=AN。

　　　　　　此时，△AMN为等腰三角形。

12．（08通州22改编）如图，在

ABCD中，AB=8cm，AD=6cm，∠DAB=60°，点M是边AD上一点，且DM=2cm，点E、F分别是边AB、BC上的点，EM、CD的延长线交于G，GF交AD于O，设AE=CF=x，

（1）试用含x的代数式表示△CGF的面积；

（2）当GF⊥AD时，求AE的值。

　　解：

（1）∵在平行四边形ABCD中CD=AB=8，BC=AD=6

　　　　　　∵DM=2，AD=6，∴AM=4，

　　　　　　取AM、ME中点P、Q，则由中位线定理知，PQ∥AE且

。

　　　　　　由AE∥GD可得PQ∥GD从而△DGM≌△PQM

　　　　　　∴

，

　　　　　　过点F作FN⊥CD于N，

　　　　　　∵∠C=∠A=60°，CF=x

　　　　　　∴

　　　　　　∴

（2）当GF⊥AD时，

　　　　　　∵AD∥BC，∠GDA=∠A=60°

　　　　　　∴∠OGD=30°，GF⊥BC

　　　　　　∴在Rt△GFC中，

　　　　　　即：

　　　　　　∴

　　　　　　∴

　　　　　　∴当GF⊥AD时，