电力电子建模与控制仿真作业.docx

电力电子建模与控制仿真作业.docx

《电力电子建模与控制仿真作业.docx》由会员分享，可在线阅读，更多相关《电力电子建模与控制仿真作业.docx（13页珍藏版）》请在冰豆网上搜索。

电力电子建模与控制仿真作业

电力电子建模与控制

基于BUCK变换器反馈控制设计

专业：

电气工程

姓名：

荏

学号：

13S053072

BUCK变换器反馈控制设计

第一部分：

设计目标

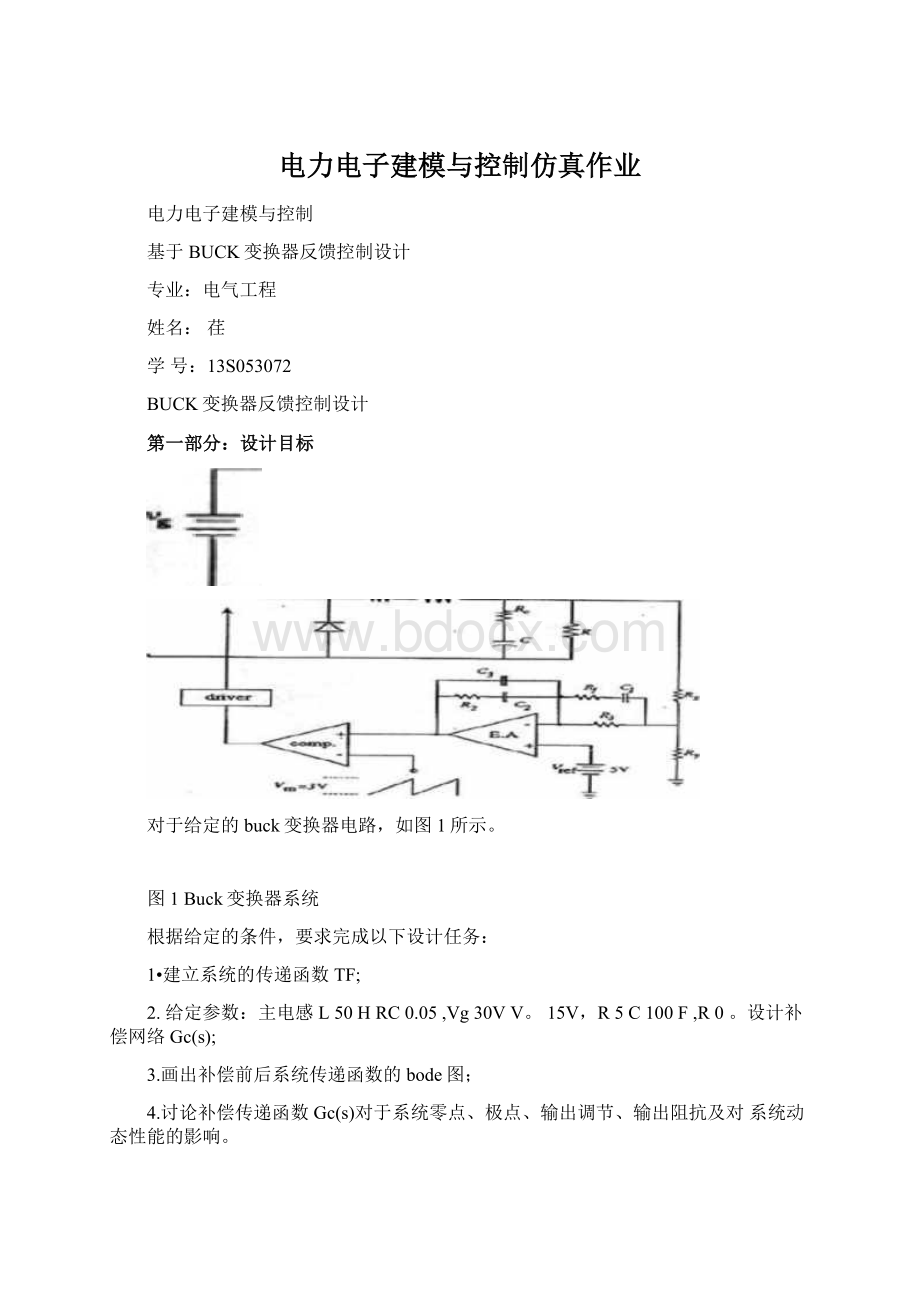
对于给定的buck变换器电路，如图1所示。

图1Buck变换器系统

根据给定的条件，要求完成以下设计任务：

1•建立系统的传递函数TF;

2.给定参数：

主电感L50HRC0.05,Vg30VV。

15V，R5C100F,R0。

设计补偿网络Gc（s）;

3.画出补偿前后系统传递函数的bode图；

4.讨论补偿传递函数Gc（s）对于系统零点、极点、输出调节、输出阻抗及对系统动态性能的影响。

第二部分：

传递函数的建立与仿真

、系统开环传递函数建立:

|«|

图2统一电路模型

表1BUCK变换器统一电路模型参数

CgnwTW

C,

i）

1.BUCK变换器占空比至输出传递函数Gvd（s）:

由以上模型和参数课求得占空比至输出的传递函数Gvd（s）:

Vg（RsRcRC）

Gvd（s）R（LRcRC）sLC（RRc）s2

（1）

2.主拓扑参数选择:

本文控制系统中反馈电阻选择：

RX1bbk,Ry1bbk，即反馈系数

1

H（s）孑开关频率为fs1bbkHz，参考电压为5V，锯齿波幅值3V。

3.工作方式：

根据BUCK变换器电流连续与断续状态的临界电感公式为

1crit

1D?

VgD2Ts

2L

D?

代入给定的参数值，可知,

电感电流

IIcrit，电路工作在连续CCM模式。

二、补偿前系统传递函数

bode图

1•原始回路增益函数G0（s）

Gb（s）H（s）G.（s）Gvd（s）

Vg（RsRRC

&RVm1s（RFCRCs2LC（RR）

（3）

代入相应数值后

1001

1001OO3

2.补偿前系统传递函数

Gb（s）

5

30（52.510s）

57.5105s25.25109s2

bode图

52.5105s

11.5105s5.05109s2

利用Matlab软件画出Gb（s）的bode图，如图3所示，从图中可以看出，系

统的幅值裕度无穷大，然而，相角裕度比价小，只有Pm=15.7deg不符合系统的

要求。

3txJeD购idTH

Gm=InfPm=157deg（at346e104rad*sj

§p-SH亠

图3补偿前系统开环系统bode图

三、系统时域内实时仿真

利用matlab/Simulink中相关的模块，搭建开环实时仿真电路图

，如图

4所示:

□Ucret曰

Tm=Le-[J75.

Fl

p=i阻Tgiii

Pul笙

GsH&alSf

+30V

Mosfet

亠.

——

E十

S[

D

4

RL

VM

图4BUCK主电路实时仿真图对应的仿真波形图如图5所示：

从仿真波形中可以看出，系统的动态特性较差，存在较大的输出超越量和较长的调节时间，稳态时，输出结果并非精确的15V，故存在较大的稳态误差。

通常选择相位裕度在45度左右，增益裕度在10dB左右，因此需要加入补偿网络Gc（s），

图中黑色线条代表输出电压波形，紫红色代表流过电感的电流波形，黄色为

矩形波发生器波形。

取其中一小段观察，如图6所示:

图6稳态时系统波形图

第三部分：

补偿网络的设计

一、补偿器传递函数

图1中所示的补偿器网络为一种有源超前--滞后补偿网络，其传递函数为

匚（訂価恃）

■™■—

ilO（）〃（R、+点）

（1+s?

?

2G）[1+*（R]+尺、）Cjj

［州（c,++尤t*g3

有源趙审J二滞后补fS网培二右两个零点，二个极点.

零点为：

Alh知2乙G人=驾"咅（&：

比）-东屆

根点为：

A，M碧=0.为虞乩厶=¥=2聞二"厂書二—kTcTq

2n

■^^sass^•

一工靠

a.A

这里R3R1,C2C1。

二、补偿器设计方法

1.采用推荐公式fgfs/5

即fg20kHz，fs为BUCK变换器的开关频率，一般说来，补偿后的回路函

数fg越大，变换器的动态速度越快。

从bode图中可以看出，原始回路函数G0（s）有两个相近的极点，极点的频率

为fp1,p21/（2JlC）2.25103Hz，可将补偿网络GJs）两个零点设计为原始回

1

103Hz。

原

Rc引起

路函数Go（s）两个相近的极点频率的1/2,即fz1fz2^fpw1.2始回路函数Go（s）有一个零点，这是由于输出滤波电容的等效串联电阻

的，此时可用补偿网络的极点来补偿，令Gc（s）的极点f

p2"ZESR5

fp310fs

2.零极点确定

两个零点：

fzif

z2

£fp1,p21.2103Hz；

三个极点：

fpi0，

P1

fp2fZESR32kHz，fp310fp122.5kHz。

3.补偿网络Gc（s）参数求取

Gc（s）的表达式为:

（11.3104s）2

cks：

15106s）（17106s）

（5）

其中kRi（CiC2）。

原始回路函数G0（s）在fg的增益为:

Go（j2fg）

11.2105

52.5105j2fgj2fg5.0510-9（j2

fg）2

0.075

补偿网络Gc（s）在fg的增益为:

Gc（j2fg）

13.3

零点fzl、fz2处的增益为:

AV

fz2

极点fp2的增益为:

Go（j2fg）

Gc（j2fg）-^200^133

M闕20荷

0.8

fp2

fg

求取补偿网络电路各元件的参数:

AV2

Rl

R3

Gc（j2fg

32^0313.3

201c3

21.3

假设R210k

，可得

R3

R2

AV2

470

2fz1R2

0.013F

C3

—1—0.01F

2fp2R3

C2

—1—707pF

2fp3R2

R1

1

2fz2C3

13.3k

4.补偿网络Gc（s）的bode图

52

58001.58s9.810s

一，、5800（11.3104s）2

Gc（s）

.J

1■!

I=

L-lJ

s（15106s）（17106s）s1.2105s23.510"1s3

对应的bode图：

'七一-

图7补偿网络Gc（s）的bode图

第四部分：

补偿后系统性能分析

一、补偿后系统的bode图

1.补偿后系统传递函数为

G（s）Gc（s）G0（s）

2.补偿后系统的bode图:

rt.~-rIMj"Tin

討「■Kb..4i・蚯gWj:

业•

•■:

I•••亠十-I.F":

-■■_11J^11111111111_

VI

"一-■■-

屜可环山*1

图8补偿后系统的bode图

此时从图中可以看出，系统的相位裕度为50.3度，幅值裕度足够大，能很

好地满足系统的稳定性和快速响应性要求。

二、补偿后系统实时仿真

1.补偿后时域内BUCK变换器仿真图

Discrete,Ffi-E

Plnstet

尺■士曷jhial

-0

——

S-aq-JT□&

1499|

Cont叶

1＞单|打

Dophyl

图9补偿后时域内

BUCK变换器仿真图

2.补偿后时域内BUCK动态波形图

3U

2S

20

15

10

CJ

0[171Qiim?

ODD3002anzBamtoqotnone盯陌oni

图10补偿后时域内BUCK动态波形图

图10表明了系统的动态性能得到了改善，响应速度和稳态精度有很大程度上的提高。

3.局部图

选取0.0059s~0.0060s时间内局部波形图进行分析。

15.02

15

HJHh

：

-3屮・■■

T

.J■'・J■

lib

..Lil.

:

J

1..L.1….1

If

JT

1

11

a?

9.2?

9.岀3.263.20S3±32朋43.3E536

-3Tirr#on#i:

'UixlO

图11局部图

纹波大约为0.06V左右，系统的稳态精度较好。

第五部分：

总结

本文通过对BUCK变换器的建模与仿真，运用反馈补偿控制知识，最终完成了一套控制补偿网络的设计，仿真结果也较好的验证了设计的正确性：

由开环系统的响应时间长，稳态精度差，超调量过大等缺点，经过补偿环节的设计之后，较好地解决了这些问题。

当然补偿设计也不是唯一的，设计过程中运用过了相关经验公式，并简化了一些条件，最终形成的结果也肯定不是最佳的。