北师大版八年级数学下册 双减分层作业设计案例 样例 第一章 三角形的证明 第二节 直角三角形.docx

北师大版八年级数学下册 双减分层作业设计案例 样例 第一章 三角形的证明 第二节 直角三角形.docx

《北师大版八年级数学下册 双减分层作业设计案例 样例 第一章 三角形的证明 第二节 直角三角形.docx》由会员分享，可在线阅读，更多相关《北师大版八年级数学下册 双减分层作业设计案例 样例 第一章 三角形的证明 第二节 直角三角形.docx（20页珍藏版）》请在冰豆网上搜索。

北师大版八年级数学下册双减分层作业设计案例样例第一章三角形的证明第二节直角三角形

单元名称

第一章三角形的证明

课题

直角三角形

节次

第1课时

作业类型

作业内容

设计意图、题源、答案

学业质量

必备知识

关键能力

质量水平

solo

难度

基础性作业

（必做）

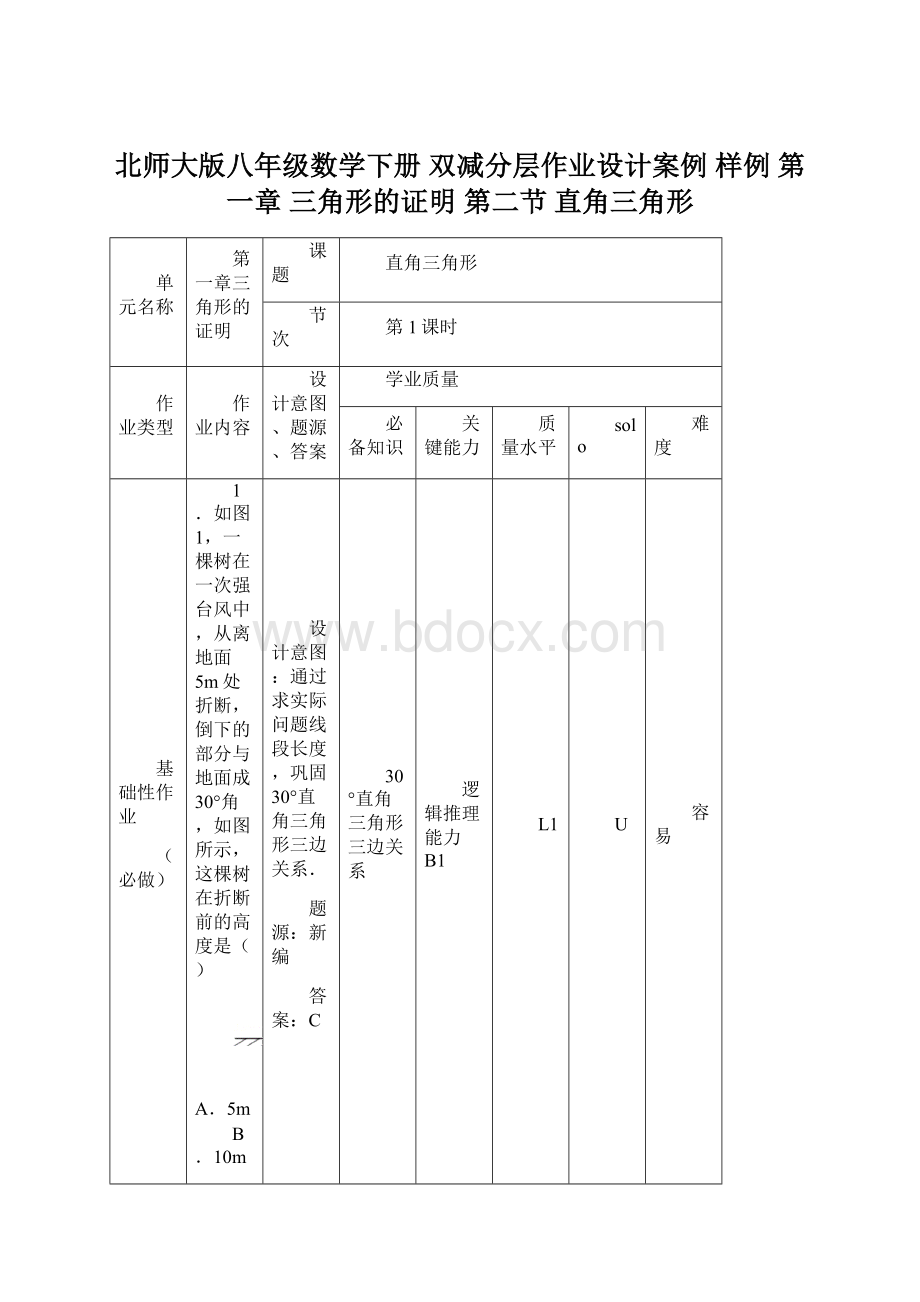
1．如图1，一棵树在一次强台风中，从离地面5m处折断，倒下的部分与地面成30°角，如图所示，这棵树在折断前的高度是（　　）

A．5m

B．10m

C．15m

D．20m

设计意图：

通过求实际问题线段长度，巩固30°直角三角形三边关系．

题源：

新编

答案：

C

30°直角三角形三边关系

逻辑推理能力B1

L1

U

容易

2．在△ABC中，∠A、∠B、∠C的对边分别为a、b、c，下列条件中，不能判断△ABC是直角三角形的是（　　）

A．a＝3，b＝4，c＝5

B．a＝b，∠C＝45°

C．∠A：

∠B：

∠C＝1：

2：

3

D．a＝

，b＝

，c＝2

设计意图：

通过判断构成直角三角形，巩固直角三角形的判定定理．

题源：

新编

答案：

C

直角三角形判定定理

直观想象能力、逻辑推理能力B1

L1

U

容易

3．下列语句：

①“等腰三角形两底角相等”的逆命题是真命题；②有两条边相等的两个直角三角形全等是假命题；③三角形的任一外角等于两个内角的和；④等腰三角形的两腰上的中线相等是真命题．其中正确的个数为（　　）

A．1个B．2个C．3个D．4个

设计意图：

通过命题判断，巩固真、假命题，逆命题概念

题源：

新编

答案：

B

真、假命题概念、三角形性质

逻辑推理能力B1

M

L2

中等

4．一块直角三角板放在两平行直线上，如图2，∠1+∠2＝　　度．

设计意图：

通过解决平行线与三角板构成的图形的角度关系问题，巩固直角三角形的锐角和90°.

题源：

新编

答案：

90°

直角三角形锐角和90°、对顶角相等

逻辑推理能力B1

L1

U

容易

5．如图3，已知钓鱼竿AC的长为10m，露在水面上的鱼线BC长为6m，某钓鱼者想看看鱼钩上的情况，把鱼竿AC转动到AC'的位置，此时露在水面上的鱼线B'C'为8m，则BB'的长为_______m．

设计意图：

通过斜边不变条件下求实际问题中线段长度，巩固勾股定理的应用.

题源：

新编

答案：

2

勾股定理

数学运算、逻辑推理能力B1

L1

U

容易

6．如图4，一块铁皮（图中阴影部分），测得AB＝3，BC＝4，CD＝12，AD＝13，∠B＝90°．求阴影部分的面积．

设计意图：

通过求不规则的阴影部分图形面积，巩固勾股定理及其逆定理

题源：

新编

答案：

详见参考答案

勾股定理、勾股逆定理、三角形面积公式

逻辑推理、数学运算能力B2

L2

M

中等

7．如图5，在△ABC中，AB＝AC，△ABC的高BH，CM交于点P．

（1）求证：

PB＝PC．

（2）若PB＝5，PH＝3，求AB．

设计意图：

通过证明线段相等、求线段长度，巩固等腰三角形的判定定理、勾股定理

题源：

新编

答案：

详见参考答案

勾股定理、等腰三角形的判定定理

逻辑推理能力、数学运算能力B2

L2

M

中等

拓展性作业

（选做）

1．如图6，在Rt△ABC中，∠B＝90°，分别以AB、AC为斜边向外作等腰直角三角形，它们的面积分别记作S1与S2，若S1＝16，S2＝25，则BC的长为______.

设计意图：

通过类似勾股树问题中求直角三角形的边长，巩固勾股定理、等腰直角三角形面积公式

题源：

选编

答案：

6

勾股定理、等腰直角三角形面积公式

数学直观能力、逻辑推理能力B2

M

L2

中等

2．将一副直角三角板按如图7所示的位置摆放，使点A、B、D在同一直线上，且EF∥AD，∠CAB＝∠EDF＝90°，∠C＝45°，∠E＝60°，如果DE＝2

，则BD＝____．

设计意图：

通过求直角三角板组合形成的线段长度，巩固特殊直角三角形的性质、勾股定理的应用，培养复杂图形中的图形分析能力

题源：

新编

答案：

特殊直角三角形三边关系、勾股定理

逻辑推理能力、数学运算能力B4

L2

E

中等

3．

（1）（操作发现）如图8-1，在边长为1个单位长度的小正方形组成的网格中，△ABC的三个顶点均在格点上．请按要求画图：

将△ABC绕点A按顺时针方向旋转90°，点B的对应点为B′，点C的对应点为C′，连接BB′，则∠AB′B＝　　．

（2）（问题解决）如图8-2，在等边三角形ABC内有一点P，且PA＝2，PB＝

，PC＝1，求∠BPC的度数和等边三角形ABC的边长；

设计意图：

通过图形的旋转条件下求角度、线段长，巩固直角三角形、等边三角形性质，培养利用基本图形解决复杂图形问题的方法．

题源：

新编

答案：

见参考答案

勾股定理、等边三角形的性质

逻辑推理能力、直观想象能力、数学建模能力B3

L3

E

较难

单元名称

第一章三角形的证明

课题

直角三角形

节次

第2课时

作业类型

作业内容

设计意图、题源、答案

学业质量

必备知识

关键能力

质量水平

solo

难度

基础性作业

（必做）

1．如图1，已知∠C＝∠D＝90°，添加一个条件，可使用“HL”判定Rt△ABC与Rt△ABD全等．以下给出的条件适合的是（　　）

A．∠ABC＝∠ABD

B．∠BAC＝∠BAD

C．AC＝AD

D．AC＝BC

设计意图：

通过在直角三角形寻找全等的条件，巩固直角三角形全等的判定定理

题源：

新编

答案：

C

直角三角形全等的判定

逻辑推理能力B1

L1

U

容易

2．如图2，用纸板挡住部分直角三角形后，也能画出与此直角三角形全等的三角形，其判断三角形全等的依据是（　　）

A．ASA

B．AAS

C．SAS

D．HL

设计意图：

通过发现直角三角形全等依据，巩固直角三角形的判定定理．

题源：

新编

答案：

A

直角三角形的判定定理.

几何直观能力、逻辑推理能力B1

L1

U

容易

3．如图3，在平面直角坐标系中，点A（﹣2，0），B（2，0），点C从点O出发，在第一象限沿射线y＝

x运动，当△ABC是直角三角形时，点C的坐标为　　．

设计意图：

通过在坐标平面内求直角三角形顶点的坐标，巩固直角三角形的判定.

题源：

新编

答案：

.

或者

直角三角形的判定

数学运算能力、逻辑推理能力B2

L2

M

中等

4．如图4，折叠长方形纸片ABCD，使点D落在边BC上的点F处，折痕为AE．已知AB＝6cm，BC＝10cm．则EC的长

为　　cm．

设计意图：

通过求折叠问题中线段长度，巩固勾股定理

题源：

新编

答案：

勾股定理、解方程

数学运算能力、逻辑推理能力B2

L2

M

中等

5．如图5，在△ABC中∠ACB＝45°，AD⊥BC于点D，

（1）请用以D为圆心，BD长为半径画弧，交线段AD于点E，连接CE，并求证：

△ABD≌△CED；

（2）在

（1）条件下，若CE是∠ACD的角平分线，求∠BAC的度数

设计意图：

通过在基本作图中寻找已知条件，证明三角形全等、求角度数，巩固三角形全等判定定理、等腰直角三角形性质

题源：

新编

答案：

详见参考答案

基本作图、三角形全等判定定理、等腰直角三角形性质

数学实际操作能力、空间想象力、数学推理论证能力B2

M

L2

中等

6．如图6，∠A＝∠B＝90°，E是AB上的一点，且AE＝BC，∠1＝∠2．

（1）求证：

△ADE≌△BEC；

（2）请写出线段CD与AD、BC之间的数量关系，并说明理由．

设计意图：

通过证明直角三角形全等、求线段数量关系，巩固直角三角形全等判定（HL）、等腰直角三角形性质

题源：

改编

答案：

详见参考答案

直角三角形全等判定定理、等腰直角三角形性质

数学直观、数学推理论证能力B2

M

L2

中等

拓展性作业

（选做）

1．如图7，△ABC中，点D为BC的中点，AB＝13，AC＝5，AD＝6，则△ABC的面积是　　．

设计意图：

通过添加辅助线（倍长中线），求三角形面积，巩固勾股定理的逆定理、三角形全等的判定、三角形面积公式.

题源：

新编

答案：

30

构造倍长中线辅助线、勾股定理的逆定理、三角形全等判定定理

逻辑推理能力B3

L3

R

较难

2．如图8，在△ABC中，∠C＝90°，AC＝BC＝3，D是AB的中点，点E、F分别在AC、BC边上运动（点E不与点A、C重合），且保持∠EDF＝90°，连接DE、DF、EF．经探索发现，四边形CEDF面积在点E、F运动过程中保持不变，其值为_____．

设计意图：

通过在定角旋转中求动图形面积，巩固等腰直角三角形添加辅助线（底边中线）方法、三角形全等判定、割补法求不规则图形面积

题源：

改编

答案：

等腰三角形的性质、三角形全等判定、割补法求不规则图形面积

空间想象能力、逻辑推理能力B4

L3

R

较难

3．

（1）如图8-1，在Rt△ABC中，∠ACB＝90°，∠A＝60°，CD平分∠ACB．

求证：

CA+AD＝BC．

小明为解决上面的问题作了如下思考：

作△ADC关于直线CD的对称图形△A′DC，

∵CD平分∠ACB，∴A′点落在CB上，且CA′＝CA，A′D＝AD．因此，要证的问题转化为只要证A′D＝A′B．请根据小明的思考写出该问题完整的证明过程．

（2）参照

（1）中小明的思考方法，解答下列问题：

如图8-2，在四边形ABCD中，AC平分∠BAD，BC＝CD＝10，AC＝17，AD＝9，求AB的长．

设计意图：

以阅读理解问题为背景，通过完善材料解答过程、迁移材料的方法解决新问题，巩固直角三角形的性质、角平分线的性质、等腰三角形三线合一的性质、勾股定理

培养学生类比的数学思想和建模的能力.

题源：

新编

答案：

见参考答案

直角三角形性质、角平分线性质、等腰三角形三线合一性质、勾股定理

数学创新、逻辑推理能力、数学运算能力B4

L3

R

较难