高等数学考试题库附答案.docx

高等数学考试题库附答案.docx

《高等数学考试题库附答案.docx》由会员分享，可在线阅读，更多相关《高等数学考试题库附答案.docx（30页珍藏版）》请在冰豆网上搜索。

高等数学考试题库附答案

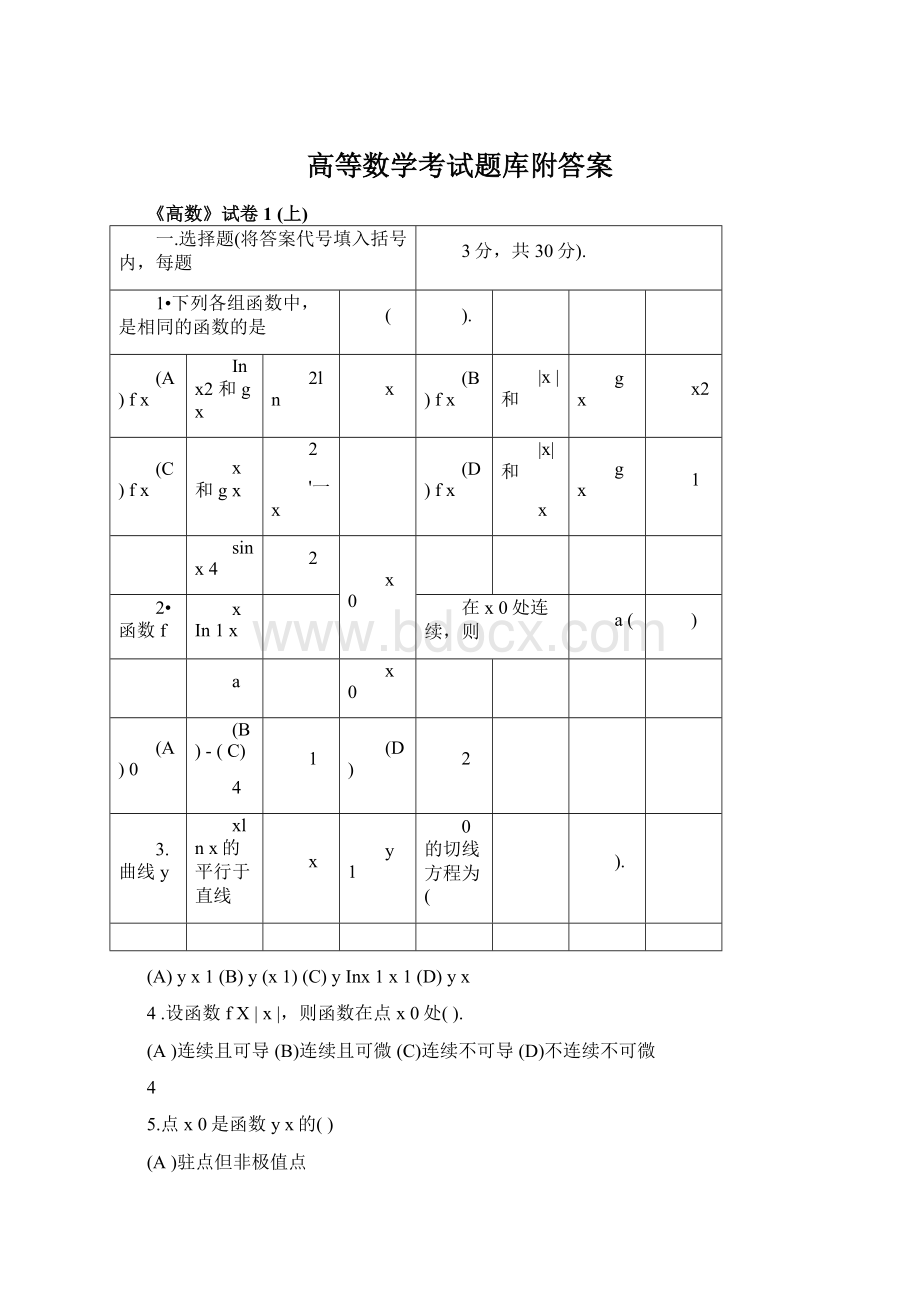
《高数》试卷1（上）

一.选择题（将答案代号填入括号内，每题

3分，共30分）.

1•下列各组函数中，是相同的函数的是

（

）.

（A）fx

Inx2和gx

2ln

x

（B）fx

|x|和

gx

x2

（C）fx

x和gx

2

'一x

（D）fx

|x|和

x

gx

1

sinx4

2

x0

2•函数f

xIn1x

在x0处连续，则

a（

）

a

x0

（A）0

（B）-（C）

4

1

（D）

2

3.曲线y

xlnx的平行于直线

x

y1

0的切线方程为（

）.

（A）yx1（B）y（x1）（C）yInx1x1（D）yx

4.设函数fX|x|，则函数在点x0处（）.

（A）连续且可导（B）连续且可微（C）连续不可导（D）不连续不可微

4

5.点x0是函数yx的（）

（A）驻点但非极值点

（B）拐点（C）驻点且是拐点

（D）驻点且是极值点

6•曲线y—的渐近线情况是（

|x|

（A）

（D）

只有水平渐近线（B）只有垂直渐近线

既无水平渐近线又无垂直渐近线

（C）既有水平渐近线又有垂直渐近线

7.

142dx的结果是

xx

（C）

（A）

dx

&的结果是（

XX

ee

（A）arctanexC（B）

arctane

（C）

（D）

ln（e'

9.下列定积分为零的是（

（A）4ac肆dx（B）

41x2

4xarcsinxdx

4

（C）

dx

（D）

x2

xsinxdx

10.设fx为连续函数，则

1

f2xdx等于

0

（A）f2

f11

（D）f1

二•填空题（每题

4分，共20分）

e2x1

1.

设函数f

0处连续,

2.

已知曲线

2处的切线的倾斜角为

-的垂直渐近线有

1

dx

x1ln2x

5.2x4sinxcosxdx

三.计算（每小题5分，共30分）

1.

求极限

彳2x

1x

lim—

xX

—xsinx

②lim

x0

2.

求曲线yInx

所确定的隐函数的导数yx.

3.

求不定积分

dx

x1x3

—dx门

③xexdx

②a0

22

■xa

四.应用题（每题10分，共20分）

1.作出函数yx33x2的图像.

尹

—

1

■1■«

r

《高数》试卷1参考答案

•选择题

1.B2.B

3.A4.C5.D6.C7.D8.A9.A10.C

.填空题

1.2

3.24.arctanlnxc5.2

三.计算题

1①e2②丄

6

2・yx

1X12

3•①—ln||C②In|x2a2x|C③exx1

2x3

四.应用题

1.略2.S18

《高数》试卷

2（上）

一.选择题（将答案代号填入括号内

1•下列各组函数中，是相同函数的是

每题3分,共3o分）

（

）.

（A）fx

（B）f

（C）fx

x（sin

2

cos

x）

（D）f

2

lnx和gx

2lnx

sin2

2•设函数f

x

2

2

x

（A）o

（B）

（C）

（D）

不存在

3设函数y

x在点xo处可导，且f

>0,曲线则y

在点

xo,fxo处的切线的倾斜角为｛

}•

（A）

（B）

（C）

锐角

（D）

钝角

4•曲线

yInx上某点的切线平行于直线

2x

3，则该点坐标是

）•

（A）

1

2，ln2

（B）2,ln1

2

（C）

1

尹2（D）

5•函数

yx2ex及图象在1,2内是（

）•

（A）单调减少且是凸的（B）单调增加且是凸的

6•以下结论正确的是（）•

（C）单调减少且是凹的

（D）单调增加且是凹的

（A）

若xo为函数yfx的驻点，则xo必为函数

yfx的极值点•

（B）

函数yfx导数不存在的点，一定不是函数

yfx的极值点•

（C）

若函数yfx在xo处取得极值，且fxo

存在,则必有f怡=o.

（D）若函数yfx在xo处连续，则fxo一定存在•

7.设函数yfx

1

（A）2x1ex

的一个原函数为X’

（B）

1

2xex

8.若fxdxF

xc,则

sinxf

（A）Fsinxc

（B）

F

sinx

1

x

9.设Fx为连续函数，则

f

dx

0

2

（A）f1f0

（B）2

f1

f0

c（C）

（C）

=（

b

e艮，则fx=（

（C）2x

cosxdx（

Fcosx

）.

）.

1

ex（D）

1

2xex

）.

c（D）

Fcosx

f0（D）2f2

10.定积分

dxab在几何上的表示（

）.

（A）线段长ba（B）线段长a

（C）矩形面积a

1（D）矩形面积b

2.填空题（每题4分,共20分）

2

ln1x

1.设fx

1cosx

a

在x0连续，则a=

2

2.设ysin

x,则dy

dsinx.

3.函数y

-1的水平和垂直渐近线共有

1

4.不定积分

xInxdx

1x2sinx1

5.定积分2x

11x2

三.计算题（每小题5分，共30分）

1.求下列极限：

1

②lim—

x

arctanx

①lim12xx

x0

1

x

y

2.求由方程y1xe

'所确定的隐函数的导数

yx.

3.求下列不定积分：

①tanxsecxdx

—dx

②a

f22

；xa

0③x2exdx

四.应用题（每题10分

共20分）

13

1.作出函数yx

3

x的图象.（要求列出表格

）

22

2.计算由两条抛物线：

yx,yx所围成的图形的面积

y

《高数》试卷2参考答案

.选择题：

.填空题：

CDCDB

1.-2

CADDD

2.2sinx

3.3

412.

4.xInx

2

12xc

4

.计算题:

1.①e2

②1

2.yx

ey

y2

5.—

2

3

3•①竽c②「rx

c③x22x2exc

1

四应用题：

1•略2.S-

3

《高数》试卷

3（上）

填空题（每小题3分,共24分）

1

1.函数y"的定义域为

2.设函数fx

sin4x

x

a,

x°,则当a=

x0

时，fx在x

3.函数f（x）

x21

x23x2

的无穷型间断点为

4.设f（x）可导,yf（ex）,则y

5.

lim亠亠

x2xx5

6.

d3・2

1xsinx,

1"72dx=

1xx1

7.

dx2etdt

dx0

8.

yyy30是

阶微分方程.

二、求下列极限（每小题5分,共15分）

2.lim导

x3x29

3.

lim

x

x

丄

2x

三、求下列导数或微分（每小题5分,

1.y—,求y（0）.

x2

3.设xyexy

共15分）

2.y

cosx

e,求dy.

四、求下列积分

求宜

dx

（每小题5分,共15分）

1.

12sinx

x

dx.

2.xln（1

x）dx.

3.

1e2xdx

0

五、

（8分）求曲线

在t-处的切线与法线方程.

cost2

六、（8分）求由曲线y

x21,直线y0,x0和x1所围成的平面图形的面积,以及此图形绕y轴旋转所得旋转体的体积.

八、（7分）求微分方程

ex满足初始条件

y10的特解.

《高数》试卷3参考答案

1.

2.

3.

x24.

exf'（ex）

6.0

7.

2xe

x28.

二阶

二二.1.原式=lim-

x0x

11

2.lim

x3x36

3.原式=Hm[（1

黑］

三.1.

y'

2

ky'（0）

2.

dy

cosx

sinxedx

3.

两边对x求写:

yxy'

y（1

y'）

xy

y'eyxyy

yxy

xexxy

四.1.原式=limx

2cosxC

2.原式=lim（1

2

一x

=-lim（1

2

2

—x

=lim（1

3.原式=1

2

2

x

x）d（J

1

2

1八

[

22

1

e

2

x）

x）

12x.0ed（2x）

sint

切线:

法线:

（x

2

（x

1）dx

2

xlim（1x

xdx

x

2x1

0

）,即y

2

12

（2x

122

（x21）2dx

0

5

x

（-

5

x）

x）

2

xlim（1

2

lim（1x）]

-（e21）

2

2

xd[lim（1

x）]

x）

七.特征方程:

x）0

1（x4

0'

28

15

1

—dx

x（

l[（x

x

x

1）e

由yx1

0,

1

1Kdx

-0

2

3

2

2x21）dx

6r

3x

e（Gcos2x

130

2i

C2sin2x）

1dx

xdxC）

C]

《高数》试卷4（上）

一、选择题（每小题3分）

1、函数yln（1x）,x2的定义域是（）

2、

3、

2,1

极限limex

x

的值是

2,1C

2,1D

2,1

sin（x

1

B、:

1）

~2~

x

不存在

D、

C、

4、

曲线

在点（1,0）处的切线方程是（

2（x1）

B、y4（x

1）

c、

4x1

D、y3（x

1）

5、

F列各微分式正确的是（

2

xdxd（x）

cos2xdxd（sin2x）

C、

dx

d（5x）

22

d（x）（dx）

6、

f（x）dx

x2cos

2

C，则

f（x）（

sin

7、

2

lnx,

dx

x

sin—

2

x

sinC

2

x

2

~~2

x

1ln

B、

c、

ln2

lnx

1（2

1

2

lnx）C

lnxC

x2

曲线y

x2

0所围成的图形绕

y轴旋转所得旋转体体积

x4dx

ydy

c、

（1y）dy

（1

x4）dx

9、

01

x

Jdx

e

C、ln

ln」

10、微分方程

c2x

2e

的一个特解为（

32x

A、ye

7

C、y

2

xe

7

2x

2x

二、填空题（每小题4分）

1、设函数yxex，贝Uy；

3sinmx2

2、如果lim,贝Um.

x02x3

3、"fcosxdx；

4、微分方程y4y4y0的通解是.

5、函数f（x）x2、x在区间0,4上的最大值是，最小值是

三、计算题（每小题5分）

1、求极限

2、求y

2

cotxlnsinx的导数;

x31

3、求函数y—的微分;

x1

dx

4、求不定积分

1品__1

e

5、求定积分1

e

Inxdx；

6、解方程月

四、应用题（每小题

10分）

2

1、求抛物线yx

2

x所围成的平面图形的面积

2、利用导数作出函数

3x2

x3

的图象•

参考答案

1、

C；

2、D；

3、C;

4、

5、C；

7、B；8、A；

9、A；

10、D；

二、1、

（x

x

2）e；

3、

（C1

C2x）e2x；

5、

三、1、

2、

cot3x

6x2

17

dx

2ln（1

12；2

.x1）C；5、2

（2）；6、y221x2C；

e

四、1、

2、

8.

—；

3

图略

《高数》试卷

5（上）

、选择题（每小题

3分）

1、函数y

1

lg（x1）

的定义域是（

2,1

0,

1,0

（0,

C、（1,0）

（0,）

1,）

2、下列各式中，极限存在的是（

I］叫cosx

B、limarctanx

x

C、limsinx

x

x

D、lim2

x

3、何1

—）x（

x

B、e2

C、

4、

曲线y

xlnx的平行于直线

0的切线方程是（

（lnx1）（x

1）

c、

（x

1）

5、

已知y

xsin3x，贝Udy

（cos3x3sin3x）dx

（sin3x

3xcos3x）dx

C、（cos3xsin3x）dx

（sin3x

xcos3x）dx

6、下列等式成立的是（

A、xdx—x1C

1

axdx

axlnxC

C、cosxdxsinxC

D、tanxdx

1x2

7、计算esinxsinxcosxdx的结果中正确的是（）.

sinx

e

sinx

ecosx

sinx

C、esinxC

sinxf

D、e（sinx1）C

1、设f（x）

1,x

axb,x

，则有limf（x）

x0

，limf（x）

x0

2

8、曲线yx,x1,y0所围成的图形绕x轴旋转所得旋转体体积V（

A、

1

0

x4dx

B

、

1

0ydy

C、

1

0

（1

y）dy

D、

1

0

（1x4

）dx

a

9、

设

a>

22

0,贝U,axdx

0

（）

A、

2

_2

12

0

1

2

a

B、—aC、

一a

D、-

a

2

4

4

10、

方程（

）是一阶线性微分方程

A、

2x

y

ln-0

B、

x

ye

y0

x

C、

（1

2x

）yysiny0

D、

xydx

（y26x）dy0

、填空题（每小题4分）

2、设yxex，贝Uy；

2

3、函数f（x）ln（1x）在区间1,2的最大值是，最小值是

13

4、xcosxdx:

1'

5、微分方程y3y2y0的通解是.

三、计算题（每小题5分）

13

1、求极限lim

（2）:

x1x1xx2

2

2、求y.1xarccosx的导数;

x

3、求函数y的微分;

.1x

4、求不定积分一dx:

x（2lnx

e

5、求定积分1

e

lnxdx:

、十2

xyy满足初始条件

1

6、求方程xy

y（?

）4的特解

四、应用题（每小题10分）

1、求由曲线

2

y2x和直线xy

0所围成的平面图形的面积

32

2、利用导数作出函数yx6x9x4

的图象•

一、1、B;

2、A;

3、D;4、C;

二、1、2

b;

2、（x2）ex;3、

一41

x“

三、1、—

;2、

arccosx1；

3

1x2

1

4、2.2lnxC；5、2（2-）；

e

四、1、9;2、图略

2

参考答案

（B

卷）

5、B;

6、

C;7、

D；

8、A；9、D;10、B

ln5,

0;

4、0；

5、

C1exC2e2x.

3、

1

dx

（1

x2）1x2

22

1

6、y

e

；

x