系统仿真上机作业.docx

系统仿真上机作业.docx

《系统仿真上机作业.docx》由会员分享，可在线阅读，更多相关《系统仿真上机作业.docx（13页珍藏版）》请在冰豆网上搜索。

系统仿真上机作业

系统仿真上机作业

学号：

04103166

姓名：

丛旭亚

系统仿真上机作业

一、计算机辅助系统分析：

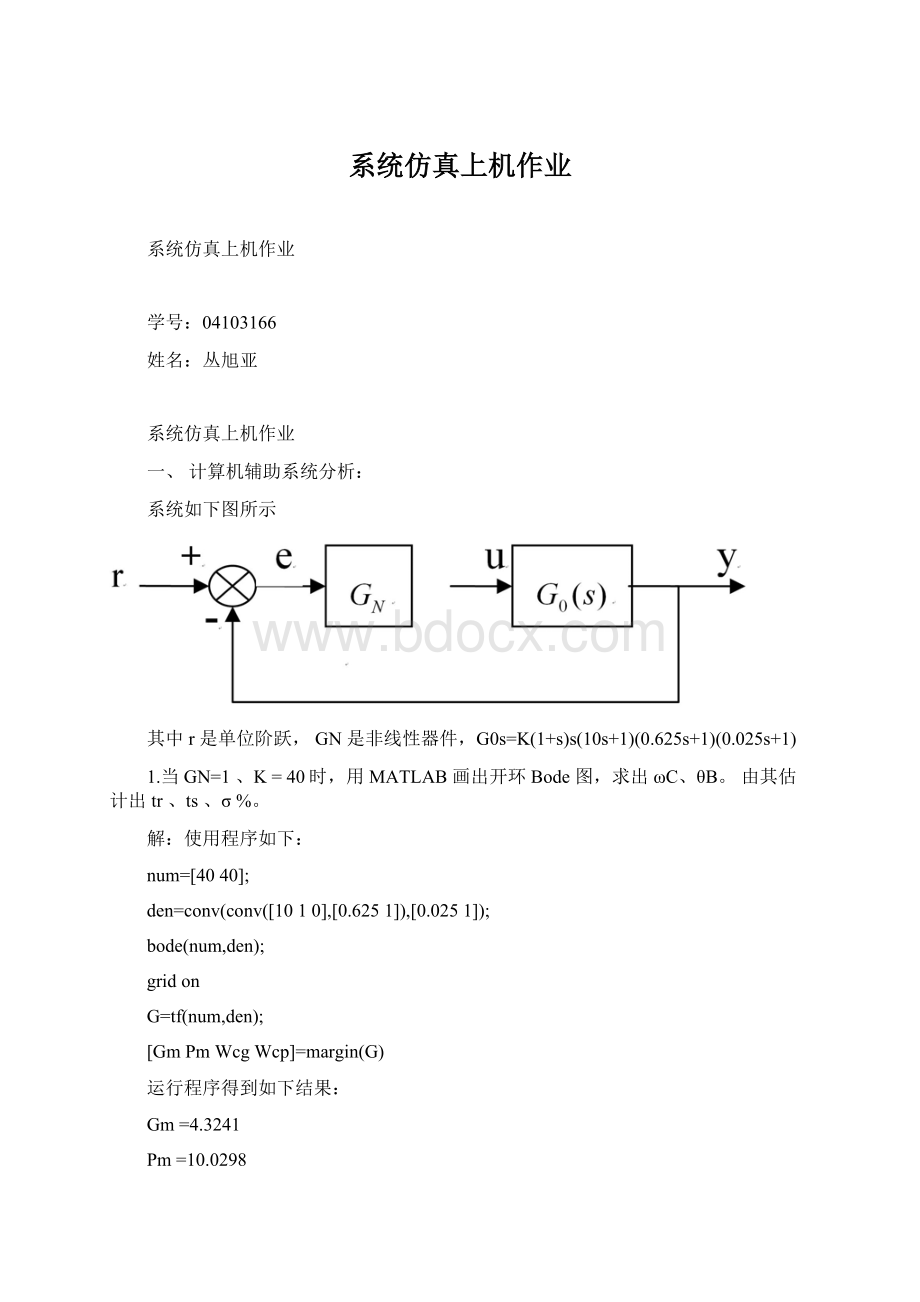
系统如下图所示

其中r是单位阶跃，GN是非线性器件，G0s=K（1+s）s（10s+1）（0.625s+1）（0.025s+1）

1.当GN=1、K=40时，用MATLAB画出开环Bode图，求出ωC、θB。

由其估计出tr、ts、σ%。

解：

使用程序如下：

num=[4040];

den=conv（conv（[1010],[0.6251]）,[0.0251]）;

bode（num,den）;

gridon

G=tf（num,den）;

[GmPmWcgWcp]=margin（G）

运行程序得到如下结果：

Gm=4.3241

Pm=10.0298

Wcg=5.1672

Wcp=2.3985

其中ωC=Wcp=2.3985rad/s，θB=Pm=10.0298°

绘制出Bode图如下：

通过系统的开环Bode图，可将系统的开环传递函数简化成G0's=40s（10s+1），其相应的闭环传递函数为GB'（s）=4010s2+s+40。

可求得ξ=0.025，ωn=2。

所以可估计出σ%=e-πξ/1-ξ2*100%=92.44%，ts=3.5/（ξωn）=70s,tr=π-βωn1-ξ2=0.80s（β=arctan1-ξ2ξ）。

2.当GN=1、K=40时，用MATLAB画出根轨迹图，并求出K=40时的闭环

极点；由其估计出tr、ts、σ%。

解：

使用程序如下：

num=[4040];

den=conv（conv（[1010],[0.6251]）,[0.0251]）;

rlocus（num,den）

G=tf（num,den）;

G1=feedback（G,1）

[p,z]=pzmap（G1）

运行程序得到如下结果：

p=

-40.1616

-0.2274+2.4146i

-0.2274-2.4146i

-1.0837

z=

-1

其中得到的p的值就是K=40时的闭环极点。

绘出根轨迹图如下：

由求得的闭环传递函数GB（s）=40（s+1）s+40.1616s+0.2274-2.4146is+0.2274+2.4146i（s+1.0837）,将其可近似为一个二阶系统GB's=40s+0.2274-2.4146is+0.2274+2.4146i≈5.882s^2+0.4548s+5.882。

可求得ξ=0.0938，ωn=2.4253。

所以可估计出σ%=e-πξ/1-ξ2*100%=74.38%，ts=3.5/（ξωn）=15.39s,tr=π-βωn1-ξ2=0.69s（β=arctan1-ξ2ξ）。

3.当GN=1，K=40时，仿真之，并由仿真结果求出tr、ts、σ%。

①用自适应变步长法

仿真结果如下：

由仿真结果可知tr=0.44s，ts=17.2s（∆=2%），σ%=81%

②用定步长RK-2法，并观察步长与仿真结果的收敛于发散关系，以及仿真精度。

当步长h=0.0498时，仿真结果收敛，仿真图如下：

由仿真结果可知tr=0.42s，ts=18.32s（∆=2%），σ%=81%

当步长h=0.0499时,仿真结果发散，仿真图如下：

4.令图中的K=40。

①GN分别为：

分别仿真之，并由仿真结果求出tr、ts、σ%。

当GN为饱和特性时，仿真结果如下：

tr=1.37s、ts=17.6s、σ%=56%。

当GN为死区特性时，仿真结果如下：

tr=0.44s，ts=32.5s、σ%=100%。

②GN=1，在G0（s）之后，反馈点之前加上

。

仿真之，并由仿真结果求出tr、ts、σ%。

tr=0.4s，ts=18.25s、σ%=100%。

③对3和4中①、②的tr、ts、σ%。

比较，并解释差异的原因。

1.通过比较第三问中自适应变步长法和定步长RK-2法的仿真结果发现，后者的ts比前者的ts要长，而前后仿真的tr、σ%相差较小。

其原因是自适应变步长法中步长hk的大小与y的变化快慢有关，当系统趋于稳定时，y变化很慢，hk变大，而定步长时hk一直为一个较小值，所以定步长RK-2法的ts要比自适应变步长法的ts长。

而在t较小的一段时间内,自适应变步长法和定步长RK-2法的步长hk都比较小，所以它们的tr、σ%相差不大。

2.4中①的非线性环节加在G0（s）之前，相当于死区特性作用在输入e（s）=r（s）-y（s）上，所以对原系统的动态性能影响较大，tr、ts、σ%与原系统相差较多；而②中的非线性环节加在G0（s）之后，则死区特性并没有直接作用于输入e（s）上，而是作用于e（s）G0（s）上，所以对原系统的动态特性影响较小，tr、ts、σ%与原系统相差较小。

二、病态系统（stiff）仿真（simulink）

Ry

r:

单位阶跃；

G（s）=1（10-4τ1s+1）（104τ2s+1）

1.用自适应变步长法（RK45）仿真之

解：

当τ1=103，τ2=10-3时。

仿真结果如下：

2.用定步长四阶龙格库塔法仿真，并试着搜索收敛的步长h的范围；若找不到h，将τ1增大，τ2减小，用定步长四阶龙格库塔法仿真，寻找h。

解：

当τ1=103，τ2=10-3时。

收敛的步长h的范围是：

h<=0.275。

当h=0.275时的仿真结果如下：

3.用病态仿真算法仿真之

以上三问，均打印出仿真曲线，计算暂态响应，并比较讨论之。

解：

当τ1=103，τ2=10-3时，由题可知Y（s）=G（s）R（s）=1s（10s+1）（0.1s+1）=1s-10099s+0.1+199s+10，则Y（t）=-10099e-0.1t+199e-10t+1。

当t=5s时，可算出Y（t）=0.387,用自适应变步长法（RK45）仿真得到的Y（t）=0.39,用定步长四阶龙格库塔法（h=0.275）仿真得到的Y（t）=0.395，用病态仿真算法仿真得到的Y（t）=0.385。

通过比较发现用病态仿真算法仿真得到的暂态响应与理论计算值最接近，自适应变步长法其次，定步长四阶龙格库塔法精度最低。

这是因为被仿真系统的τmaxτmin=100>50，该系统是一个病态系统，所以用病态仿真算法仿真最精确，而RK45和RK4则都会产生一定的误差。

三．计算机辅助控制器设计：

A

R（s）+Y（s）

-B

其中Gs=10s（s+1）

要求：

开环θB≥45°，ωc≥4.2，且tr≤0.4s，ts≤1.5s，σ%≤25%

1.开关处于A时，系统性能满足上述要求否？

解：

编写如下程序求解系统的各项指标如下：

num=[10];

den=[110];

G=tf（num,den）;

[GmPmWcgWcp]=margin（G）

num=[10];

den=[110];

sys=tf（num,den）;

sys=feedback（sys,1）;

[y,t]=step（sys）;

ytr=find（y>=1）;

risetime=t（ytr

（1））

[ymax,tp]=max（y）;

maxovershoot=ymax-1

s=length（t）;

whiley（s）>0.98&y（s）<1.02

s=s-1;

end

settlingtime=t（s+1）

程序运行结果为：

Gm=Inf

Pm=17.9642

Wcg=Inf

Wcp=3.0842

risetime=0.6447

maxovershoot=0.6045

settlingtime=7.2762

由此可见θB=Pm=17.9642°<45°，ωc=3.0842<4.2，tr=0.6447s>0.4s，ts=7.2762s>1.5s，σ%=60.45%>25%，均不符合要求。

2.开关处于B时，计算机辅助设计GC（s），使系统性能满足上述要求。

由第一问可知，要使系统满足上述要求必须串联超前校正环节。

设计频率法超前校正的MATLAB子函数如下：

functionGc=plsj（G,kc,yPm）

G=tf（G）;

[mag,pha,w]=bode（G*kc）;

Mag=20*log10（mag）;

[Gm,Pm.Wcg,Wcp]=margin（G*kc）;

phi=（yPm-getfield（Pm,'Wcg'））*pi/180;

alpha=（1+sin（phi））/（1-sin（phi））;

Mn=-10*log10（alpha）;

Wcgn=spline（Mag,w,Mn）;

T=1/（Wcgn*sqrt（alpha））;

Tz=alpha*T;

Gc=tf（[Tz1],[T1]）;

End

主程序如下：

num=[10];

den=[110];

G=tf（num,den）;

kc=2;thegreater,thebetter!

yPm=18+40;

Gc=plsj（G,kc,yPm）

这一步得到的串联超前校正环节传递函数GCs=0.3503s+10.05938s+1，校正环节的增益为2。

Gc1=feedback（G*Gc*kc,1）;

[Gm,Pm,Wcg,Wcp]=margin（G*Gc*kc）

[y,t]=step（Gc1）;

ytr=find（y>=1）;

risetime=t（ytr

（1））

[ymax,tp]=max（y）;

maxovershoot=ymax-1

s=length（t）;

whiley（s）>0.98&y（s）<1.02

s=s-1;

end

settlingtime=t（s+1）

程序运行结果如下：

Gm=Inf

Pm=53.4487

Wcg=Inf

Wcp=6.9337

risetime=0.2554

maxovershoot=0.2021

settlingtime=0.9398

即θB=Pm=53.4487°>45°，ωc=6.9337>4.2，tr=0.2554s<0.4s，ts=0.9398s<1.5s，σ%=20.21%<25%，均符合要求。

校正后仿真结果如下图所示：

四、一级倒立摆仿真收敛性研究

仿真在位移x处加阶跃干扰的倒立摆非线性模型（已建好，但仿真不成功），

除了倒立摆系统和控制器不能改动，其他地方可以酌情修改，如更改算法等等。

要求：

1.仿真收敛；

2.说明修改过程并解释物理意义；

3.说明如何验证仿真结果（不）稳定是系统本身（不）稳定还是仿真原因造成的？

解：

在位移X处加如下阶跃干扰，如下图所示：

其物理意义是：

在时间t=1s时,使小车的位移发生由0到0.15的突变。

在t=0时刻，在输入端加一个单位阶跃信号作为输入的外力F。

采用自适应变步长ode45算法，得到的仿真结果如下：

位移x:

摆杆与竖直方向的夹角θ:

有仿真结果可知仿真收敛。

通过理论计算可以得到系统本身的稳定性，若该结果与仿真结果一致，则可以验证仿真结果的（不）稳定是系统（不）稳定造成的；若该结果图仿真结果不一致，则可以验证仿真结果的（不）稳定是仿真原因造成的。