乘法公式完全平方公式专题训练试题精选三附答案.docx

乘法公式完全平方公式专题训练试题精选三附答案.docx

《乘法公式完全平方公式专题训练试题精选三附答案.docx》由会员分享，可在线阅读，更多相关《乘法公式完全平方公式专题训练试题精选三附答案.docx（33页珍藏版）》请在冰豆网上搜索。

乘法公式完全平方公式专题训练试题精选三附答案

完全平方公式专题训练试题精选（三）

一．选择题（共30小题）

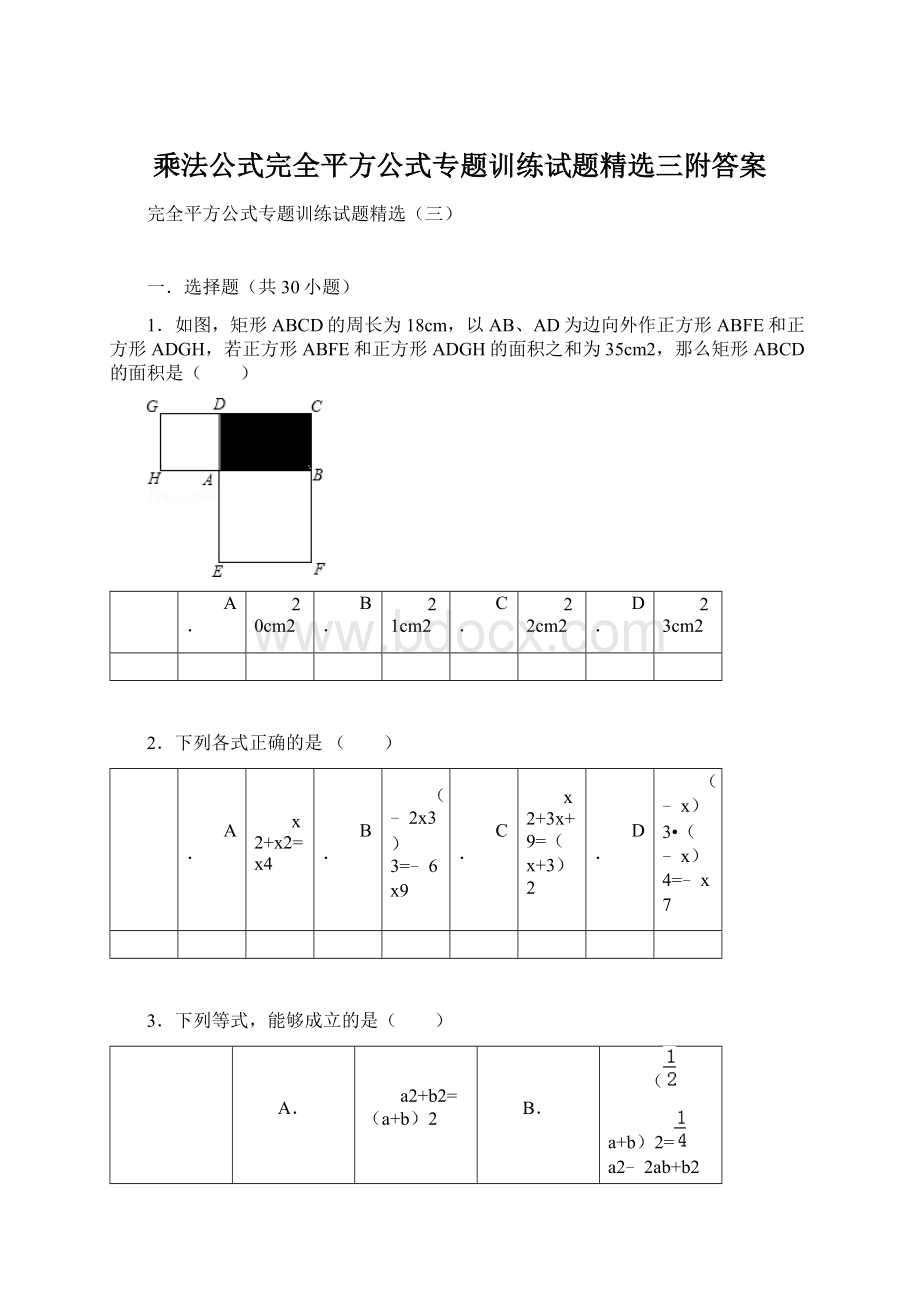
1．如图，矩形ABCD的周长为18cm，以AB、AD为边向外作正方形ABFE和正方形ADGH，若正方形ABFE和正方形ADGH的面积之和为35cm2，那么矩形ABCD的面积是（　　）

A．

20cm2

B．

21cm2

C．

22cm2

D．

23cm2

2．下列各式正确的是（　　）

A．

x2+x2=x4

B．

（﹣2x3）3=﹣6x9

C．

x2+3x+9=（x+3）2

D．

（﹣x）3•（﹣x）4=﹣x7

3．下列等式，能够成立的是（　　）

A．

a2+b2=（a+b）2

B．

（

a+b）2=

a2﹣2ab+b2

C．

（2a﹣b）2=4a2﹣4ab+b2

D．

（a+b+c）2=（a﹣b﹣c）2

4．小明在利用完全平方公式计算一个二项整式的平方时，不小心用墨水把中间一项的系数染黑了，得到正确的结果为4a2■ab+9b2，你认为这个二项整式应是（　　）

A．

2a+3b

B．

2a﹣3b

C．

2a±3b

D．

4a±9b

5．下列计算：

①

+

=

；②2a3•3a2=6a6；③（2x+y）（x﹣3y）=2x2﹣5xy﹣3y2；④（x+y）2=x2+y2．其中计算错误的个数是（　　）

A．

O个

B．

l个

C．

2个

D．

3个

6．对于任意有理数a，b，现用“☆”定义一种运算：

a☆b=a2﹣b2，根据这个定义，代数式（x+y）☆y可以化简为（　　）

A．

xy+y2

B．

xy﹣y2

C．

x2+2xy

D．

x2

7．已知，（x+y）2=16，（x﹣y）2=8，那么xy的值是（　　）

A．

﹣2

B．

2

C．

﹣3

D．

3

8．如果

，那么

的值是（　　）

A．

2

B．

4

C．

0

D．

﹣4

9．（x+k）2=x2+2kx+4，则k的值是（　　）

A．

﹣2

B．

2

C．

±2

D．

3

10．运算结果为2mn﹣m2﹣n2的是（　　）

A．

（m﹣n）2

B．

﹣（m﹣n）2

C．

﹣（m+n）2

D．

（m+n）2

11．若a﹣b=2，a﹣c=1，则（2a﹣b﹣c）2+（c﹣a）2的值是（　　）

A．

9

B．

10

C．

2

D．

1

12．若x2+ax+9=（x+3）2，则a的值为（　　）

A．

3

B．

±3

C．

6

D．

±6

13．已知x2+y2=13，xy=6，则x+y的值是（　　）

A．

±5

B．

±1

C．

±

D．

1或

14．（a﹣b+c）（﹣a+b﹣c）等于（　　）

A．

﹣（a﹣b+c）2

B．

c2﹣（a﹣b）2

C．

（a﹣b）2﹣c2

D．

c2﹣a+b2

15．若a+b=2，a2+b2=2，请你判断下面a、b关系表示正确的式子是（　　）

A．

a=2b

B．

a=﹣2b

C．

a=b

D．

ab=1

16．如果x2+y2=8，x+y=3，则xy=（　　）

A．

1

B．

C．

2

D．

﹣

17．若x2是一个正整数的平方，则它后面一个整数的平方应当是（　　）

A．

x2+1

B．

x+1

C．

x2+2x+1

D．

x2﹣2x+1

18．若用简便方法计算19992，应当用下列哪个式子？

（　　）

A．

（2000﹣1）2

B．

（2000﹣1）（2000+1）

C．

（1999+1）（1999﹣1）

D．

（1999+1）2

19．下列等式一定成立的是（　　）

A．

（1﹣b）2=1﹣b+b2

B．

（a+3）2=a2+9

C．

（x+

）2=x2+

+2

D．

（x﹣3y）2=x2﹣9y

20．下列式子满足完全平方公式的是（　　）

A．

（3x﹣y）（﹣y﹣3x）

B．

（3x﹣y）（3x+y）

C．

（﹣3x﹣y）（y﹣3x）

D．

（﹣3x﹣y）（y+3x）

21．下列等式中，成立的是（　　）

A．

（a+b）2=a2+b2

B．

（a﹣b）2=a2﹣b2

C．

（a+b）2=a2+b（2a+b）

D．

（﹣a+b）（a﹣b）=a2﹣b2

22．计算（﹣cd﹣3）2的结果为（　　）

A．

c2d2﹣6cd+9

B．

﹣c2d2﹣6cd+9

C．

c2d2+6cd+9

D．

c2d2+6cd﹣9

23．下列各式中与2xy﹣x2﹣y2相等的是（　　）

A．

（x﹣y）2

B．

﹣（x+y）2

C．

﹣（x﹣y）2

D．

（x+y）2

24．如果ax2+2x+

=（2x+

）2+m，则a，m的值分别是（　　）

A．

2，0

B．

2，

C．

4，

D．

，4

25．若等式（x﹣4）2=x2﹣8x+m2成立，则m的值是（　　）

A．

16

B．

4

C．

﹣4

D．

4或﹣4

26．下列各式计算结果为2xy﹣x2﹣y2的是（　　）

A．

（x﹣y）2

B．

（﹣x﹣y）2

C．

﹣（x+y）2

D．

﹣（x﹣y）2

27．如果

，则

=（　　）

A．

25

B．

23

C．

21

D．

27

28．若a+b=0，ab=11，则a2﹣ab+b2的值为（　　）

A．

11

B．

﹣11

C．

﹣33

D．

33

29．若x=a2﹣2a+2，则对于所有的x值，一定有（　　）

A．

x＜0

B．

x≤0

C．

x＞0

D．

x的正负与a值有关

30．与（

﹣

）2的结果一样的是（　　）

A．

（x+y）2﹣xy

B．

（

+

）2+xy

C．

（x﹣y）2

D．

（x+y）2﹣xy

完全平方公式专题训练试题精选（三）

参考答案与试题解析

一．选择题（共30小题）

1．如图，矩形ABCD的周长为18cm，以AB、AD为边向外作正方形ABFE和正方形ADGH，若正方形ABFE和正方形ADGH的面积之和为35cm2，那么矩形ABCD的面积是（　　）

A．

20cm2

B．

21cm2

C．

22cm2

D．

23cm2

考点：

完全平方公式．菁优网版权所有

专题：

计算题．

分析：

设出矩形的长与宽分别为x、y，根据两正方形的面积和矩形的周长列出方程，然后结合完全平方公式求出xy的值，也就是矩形的面积．

解答：

解：

设AB=x，AD=y，根据题意，得

x2+y2=35①，

2（x+y）=18②，

由①，得

（x+y）2﹣2xy=35，

∴2xy=81﹣35=46，

∴xy=23，即矩形ABCD的面积是23cm2．

故选D．

点评：

本题考查了完全平方公式的应用．解题时，熟练运用正方形的面积公式和长方形的周长公式表示等式，再根据完全平方公式变形代值计算，不需要求出矩形的长与宽的具体数值，只要求出它们的积即可．

2．下列各式正确的是（　　）

A．

x2+x2=x4

B．

（﹣2x3）3=﹣6x9

C．

x2+3x+9=（x+3）2

D．

（﹣x）3•（﹣x）4=﹣x7

考点：

完全平方公式；合并同类项；同底数幂的乘法；幂的乘方与积的乘方．菁优网版权所有

分析：

合并同类项只把同类项的系数相加，幂的乘方与积的乘方把积的因式分别乘方，同底数幂的乘法是底数不变指数相加，完全平方公式要记准它的结构形式．

解答：

解：

A、x2+x2=2x2故A选项错误；

B、（﹣2x3）3=﹣8x9故B选项错误；

C、（x+3）2=x2+6x+9故C选项错误；

D、（﹣x）3•（﹣x）4=﹣x7故D选项正确．

故选D．

点评：

本题主要考查了合并同类项、完全平方公式、同底数幂的乘法、幂的乘方与积的乘方的相关运算．

3．下列等式，能够成立的是（　　）

A．

a2+b2=（a+b）2

B．

（

a+b）2=

a2﹣2ab+b2

C．

（2a﹣b）2=4a2﹣4ab+b2

D．

（a+b+c）2=（a﹣b﹣c）2

考点：

完全平方公式．菁优网版权所有

分析：

利用完全平方公式求解判定．

解答：

解：

A、a2+b2+2ab=（a+b）2，故A选项错误；

B、（

a+b）2=

a2+ab+b2，故B选项错误；

C、（2a﹣b）2=4a2﹣4ab+b2，故C选项正确；

D、（a+b+c）2≠（a﹣b﹣c）2，故D选项错误．

故选：

C．

点评：

本题主要考查了完全平方公式，解题的关键是熟记完全平方公式．

4．小明在利用完全平方公式计算一个二项整式的平方时，不小心用墨水把中间一项的系数染黑了，得到正确的结果为4a2■ab+9b2，你认为这个二项整式应是（　　）

A．

2a+3b

B．

2a﹣3b

C．

2a±3b

D．

4a±9b

考点：

完全平方公式．菁优网版权所有

分析：

运用完全平方公式求出（2a±3b）2对照求解．

解答：

解：

由（2a±3b）2=4a2±12ab+9b2，

∴染黑的部分为±12ab，

故选：

C．

点评：

本题主要考查完全平方公式，解题的关键是熟记法则．

5．下列计算：

①

+

=

；②2a3•3a2=6a6；③（2x+y）（x﹣3y）=2x2﹣5xy﹣3y2；④（x+y）2=x2+y2．其中计算错误的个数是（　　）

A．

O个

B．

l个

C．

2个

D．

3个

考点：

完全平方公式；实数的运算；单项式乘单项式；多项式乘多项式．菁优网版权所有

分析：

①根据二次根式的计算法则计算；

②同底数幂的乘法，底数不变，指数相加；

③多项式乘以多项式的计算法则；

④完全平方公式：

（a+b）2=a2+2ab+b2．

解答：

解：

①因为

和

不是同类二次根式，所以不能合并同类项，故该选项错误；

②2a3•3a2=6a3+2=6a5．故该选项错误；

③（2x+y）（x﹣3y），

=2x2+xy﹣6xy﹣3y2=2x2﹣5xy﹣3y2．故本选项正确；

④（x+y）2=x2+2xy+y2．故该选项错误；

综上所述，计算错误的是①②④，共三个，

故选D．

点评：

本题综合考查了单项式乘单项式、多项式乘以多项式、完全平方公式及实数的运算．解答此题时注意不要丢掉完全平方公式（a+b）2=a2+2ab+b2中的2ab项．

6．对于任意有理数a，b，现用“☆”定义一种运算：

a☆b=a2﹣b2，根据这个定义，代数式（x+y）☆y可以化简为（　　）

A．

xy+y2

B．

xy﹣y2

C．

x2+2xy

D．

x2

考点：

完全平方公式．菁优网版权所有

专题：

新定义．

分析：

由题目中给出的运算方法，即可推出原式=x2+2xy，通过计算即可推出结果．

解答：

解：

（x+y）☆y

=（x+y）2﹣y2

=x2+2xy+y2﹣y2

=x2+2xy．

故选：

C．

点评：

此题主要考查了完全平方公式，解题的关键是根据题意掌握新运算的规律．

7．已知，（x+y）2=16，（x﹣y）2=8，那么xy的值是（　　）

A．

﹣2

B．

2

C．

﹣3

D．

3

考点：

完全平方公式．菁优网版权所有

分析：

根据完全平方公式，对已知的算式分别整理，然后再相减便可得答案．

解答：

解；∵（x+y）2=x2+2xy+y2=16，（x﹣y）2=x2﹣2xy+y2=8

∴（x2+2xy+y2）﹣（x2﹣2xy+y2）=8

即4xy=8，

∴xy=2．

故选B．

点评：

本题主要考查完全平方公式，熟记公式变形是解题的关键．

8．如果

，那么

的值是（　　）

A．

2

B．

4

C．

0

D．

﹣4

考点：

完全平方公式．菁优网版权所有

专题：

计算题．

分析：

此题首先通过添项运用完全平方公式化为含a+

的代数式，然后代入求值．

解答：

解：

a2+

=a2+2•a•

+

﹣2•a•

=

﹣2，

当a+

=2时，

上式=22﹣2=2．

故选：

A．

点评：

此题考查的知识点是完全平方公式，构建完全平方公式是关键．

9．（x+k）2=x2+2kx+4，则k的值是（　　）

A．

﹣2

B．

2

C．

±2

D．

3

考点：

完全平方公式．菁优网版权所有

分析：

运用完全平方公式求解即可．

解答：

解：

∵（x+k）2=x2+2kx+4，

∴k=±2，

故选：

C．

点评：

本题主要考查了完全平方公式，解题的关键是熟记公式．

10．运算结果为2mn﹣m2﹣n2的是（　　）

A．

（m﹣n）2

B．

﹣（m﹣n）2

C．

﹣（m+n）2

D．

（m+n）2

考点：

完全平方公式．菁优网版权所有

专题：

计算题．

分析：

根据完全平方公式（a±b）2=a2±2ab+b2即可解答．

解答：

解：

2mn﹣m2﹣n2=﹣（m2﹣2mn+n2）=﹣（m﹣n）2．

故选B．

点评：

本题是完全平方公式的应用，两数的平方和，再加上或减去它们积的2倍，就构成了一个完全平方式．解此题的关键是提出负号后把完全平方公式上对应位置的数找出来，对号入座，即可得出正确的式子．

11．若a﹣b=2，a﹣c=1，则（2a﹣b﹣c）2+（c﹣a）2的值是（　　）

A．

9

B．

10

C．

2

D．

1

考点：

完全平方公式．菁优网版权所有

分析：

完全平方公式：

（a±b）2=a2±2ab+b2，条件a﹣b=2，a﹣c=1，所以要把（2a﹣b﹣c）2+（c﹣a）2拆分组合成a﹣b，a﹣c的形式，直接代入即可解题．

解答：

解：

（2a﹣b﹣c）2+（c﹣a）2，

=（a﹣b+a﹣c）2+（a﹣c）2，

=（2+1）2+12，

=10．

故选B．

点评：

该题主要是考查整体代入思想和完全平方公式的运用，通过观察，利用公式简化计算．关键是把（2a﹣b﹣c）2+（c﹣a）2进拆分组合成a﹣b，a﹣c的形式．

12．若x2+ax+9=（x+3）2，则a的值为（　　）

A．

3

B．

±3

C．

6

D．

±6

考点：

完全平方公式．菁优网版权所有

专题：

计算题．

分析：

根据题意可知：

将（x+3）2展开，再根据对应项系数相等求解．

解答：

解：

∵x2+ax+9=（x+3）2，

而（x+3）2=x2+6x+9；

即x2+ax+9=x2+6x+9，

∴a=6．

故选C．

点评：

本题主要考查完全平方公式的应用，利用对应项系数相等求解是解题的关键．

13．已知x2+y2=13，xy=6，则x+y的值是（　　）

A．

±5

B．

±1

C．

±

D．

1或

考点：

完全平方公式．菁优网版权所有

专题：

计算题．

分析：

根据完全平方公式和已知条件，先求出x+y的平方，然后再开平方即可求出x+y的值．

解答：

解：

∵x2+y2=13，xy=6，

∴（x+y）2=x2+2xy+y2=13+2×6，

∴（x+y）2=25，

解得x+y=±5．

故选A．

点评：

本题主要考查了完全平方公式，注意（x+y）2=25时，25的平方根是±5而不是只有5．

14．（a﹣b+c）（﹣a+b﹣c）等于（　　）

A．

﹣（a﹣b+c）2

B．

c2﹣（a﹣b）2

C．

（a﹣b）2﹣c2

D．

c2﹣a+b2

考点：

完全平方公式．菁优网版权所有

分析：

两个式子的各项都互为相反数，因而两个式子互为相反数，可以把其中一个式子提出一个符号，变化成相同的式子，再利用完全平方公式计算．

解答：

解：

（a﹣b+c）（﹣a+b﹣c）=﹣（a﹣b+c）2．

故选A．

点评：

本题主要考查了完全平方公式，注意两个式子的各项互为相反数，可以通过对一项提取负号变化成相同．

15．若a+b=2，a2+b2=2，请你判断下面a、b关系表示正确的式子是（　　）

A．

a=2b

B．

a=﹣2b

C．

a=b

D．

ab=1

考点：

完全平方公式．菁优网版权所有

专题：

计算题．

分析：

利用完全平方和公式来求的a与b的数量关系．

解答：

解：

∵a+b=2，a2+b2=2，

∴（a+b）2=a2+2ab+b2，

∴4=2+2ab，解得ab=1．

故选D．

点评：

本题考查了完全平方公式，熟记公式的几个变形公式对解题大有帮助．

16．如果x2+y2=8，x+y=3，则xy=（　　）

A．

1

B．

C．

2

D．

﹣

考点：

完全平方公式．菁优网版权所有

专题：

整体思想．

分析：

首先把x+y=3两边同时平方得到x2+2xy+y2=9，然后把x2+y2=8代入其中即可求出xy的值．

解答：

解：

∵x+y=3，

∴x2+2xy+y2=9，

而x2+y2=8，

∴2xy=﹣9+8=﹣1，

∴xy=﹣

．

故选D．

点评：

此题主要考查了利用完全平方公式进行代数变形，然后利用整体代值的思想即可解决问题．

17．若x2是一个正整数的平方，则它后面一个整数的平方应当是（　　）

A．

x2+1

B．

x+1

C．

x2+2x+1

D．

x2﹣2x+1

考点：

完全平方公式．菁优网版权所有

专题：

计算题．

分析：

首先找到它后面那个整数x+1，然后根据完全平方公式解答．

解答：

解：

x2是一个正整数的平方，它后面一个整数是x+1，

∴它后面一个整数的平方是：

（x+1）2=x2+2x+1．

故选C．

点评：

本题主要考查完全平方公式，熟记公式结构是解题的关键．完全平方公式：

（a±b）2=a2±2ab+b2．

18．若用简便方法计算19992，应当用下列哪个式子？

（　　）

A．

（2000﹣1）2

B．

（2000﹣1）（2000+1）

C．

（1999+1）（1999﹣1）

D．

（1999+1）2

考点：

完全平方公式．菁优网版权所有

分析：

根据完全平方公式与平方差公式的应用，即可求得答案．

解答：

解：

A、（2000﹣1）2=19992，故本选项正确；

B、（2000﹣1）（2000+1）=20002﹣1，故本选项错误；

C、（1999+1）（1999﹣1）=19992﹣1，故本选项错误；

D、（1999+1）2=20002，19992=（2000﹣1）2，故本选项错误．

故选A．

点评：

此题考查了完全平方公式与平方差公式的应用．熟记公式是准确求解此题的关键．

19．下列等式一定成立的是（　　）

A．

（1﹣b）2=1﹣b+b2

B．

（a+3）2=a2+9

C．

（x+

）2=x2+

+2

D．

（x﹣3y）2=x2﹣9y

考点：

完全平方公式．菁优网版权所有

分析：

根据完全平方公式判断即可．

解答：

解：

A、（1﹣b）2=1﹣2b+b2，故本项错误；

B、（a+3）2=a2+6a+9，故本项错误；

C、（x+

）2=x2+

+2，本项正确；

D、（x﹣3y）2=x2﹣6xy+9y2，故本项错误，

故选：

C．

点评：

本题主要考查完全平方公式，熟记公式是解题的关键．

20．下列式子满足完全平方公式的是（　　）

A．

（3x﹣y）（﹣y﹣3x）

B．

（3x﹣y）（3x+y）

C．

（﹣3x﹣y）（y﹣3x）

D．

（﹣3x﹣y）（y+3x）

考点：

完全平方公式．菁优网版权所有

分析：

首先将各式变形，再根据完全平方公式的知识求解即可求得答案．

解答：

解：

A、∵（3x﹣y）（﹣y﹣3x）=﹣（3x﹣y）（y+3x），∴不是完全平方式，故本选项错误；

B、（3x﹣y）（3x+y），不是完全平方式，故本选项错误；

C、∵（﹣3x﹣y）（y﹣3x）=（3x+y）（3x﹣y），∴不是完全平方式，故本选项错误；

D、∵（﹣3x﹣y）（y+3x）=﹣（3x+y）（y+3x）=﹣（3x+y）2，∴是完全平方式，故本选项正确．

故选D．

点评：

此题考查了完全平方公式．解题的关键是注意符号的变化．