矩阵问题讲解.docx

矩阵问题讲解.docx

《矩阵问题讲解.docx》由会员分享，可在线阅读，更多相关《矩阵问题讲解.docx（17页珍藏版）》请在冰豆网上搜索。

矩阵问题讲解

矩阵问题

1.

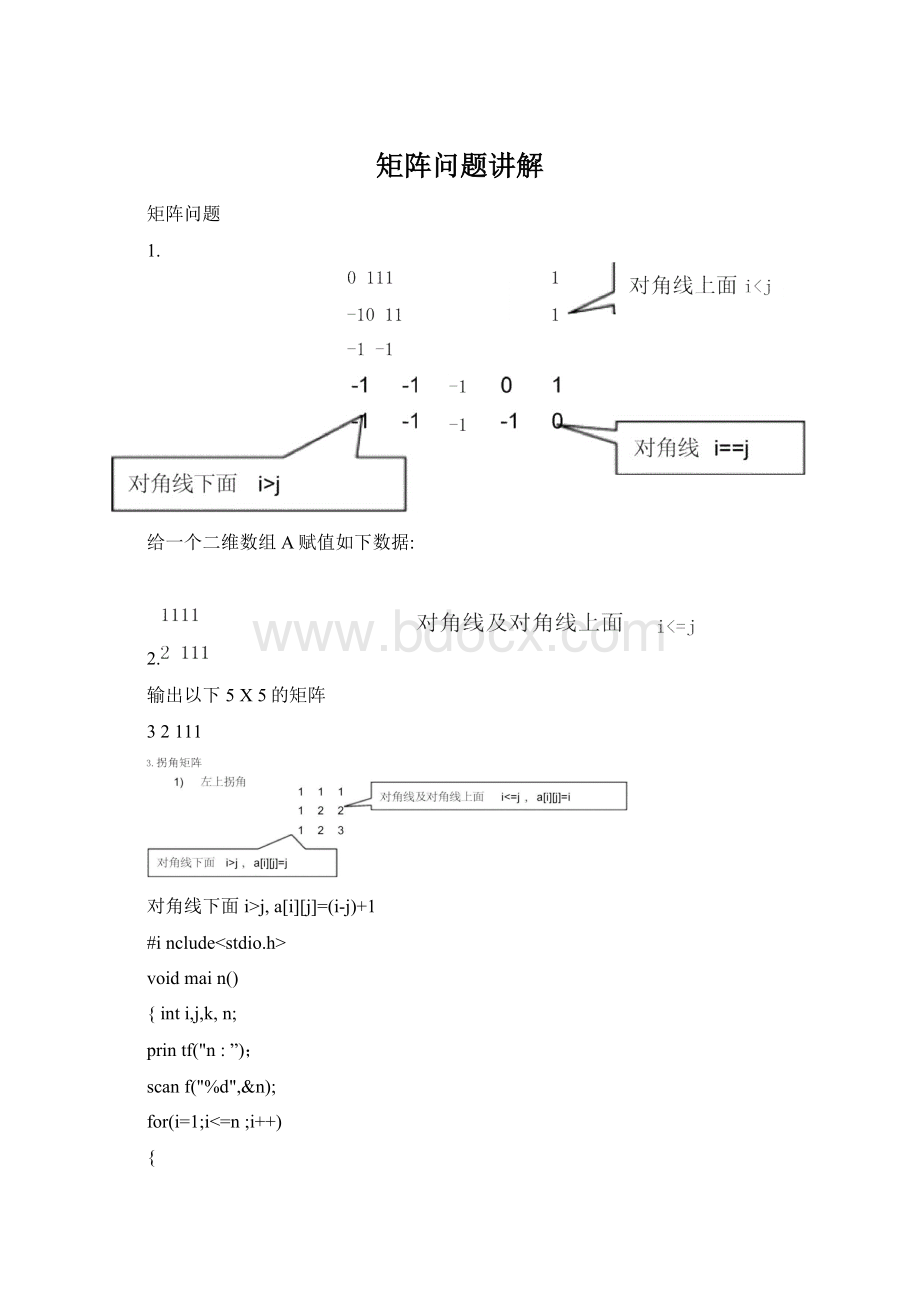
给一个二维数组A赋值如下数据:

2.

输出以下5X5的矩阵

32111

对角线下面i>j,a[i][j]=（i-j）+1

#include

voidmain（）

{inti,j,k,n;

printf（"n:

”）；

scanf（"%d",&n）;

for（i=1;i<=n;i++）

{

for（j=1;j<=n;j++）

{k=i>j?

j:

i;

printf（"%4d",k）;

}

printf（"\n"）;

2）右下拐角

对角线及对角线上面i<=j,a[i][j]=n+1-j

对角线下面i>j,a[i][j]=n+1-i——#include

voidmain（）

{inti,j,k,n;

printf（"n:

”）；scanf（"%d",&n）;for（i=1;i<=n;i++）

{

for（j=1;j<=n;j++）

{if（i<=j）

printf（"%4d",n+1-j）;else

printf（"%4d",n+1-i）;}

printf（"\n"）;

}

}

3）左下拐角

副对角线上面i+j=n+1,a[i][j]=j

23

#include

22

voidmain（）

{inti,j,k,n;

printf（"n:

"）;

scanf（"%d",&n）;

for（i=1;i<=n;i++）

{

for（j=1;j<=n;j++）

{if（i+j<=n+1）

printf（"%4d",j）;

else

printf（"%4d",n+1-i）;}

printf（"\n"）;

4）右上拐角

副对角线上面i+j=n+1,a[i][j]=i#include

1

1

1副对角线及其下面i+j=n+1,a[i][j]=n+1-j

voidmain（）

{inti,j,k,n;

printf（"n:

”）；

scanf（"%d",&n）;

for（i=1;i<=n;i++）

{

for（j=1;j<=n;j++）

{if（i+j<=n+1）

printf（"%4d",i）;

else

printf（"%4d",n+1-j）;

}

printf（"\n"）;

}

}

4.回形矩阵

11111

12221

12321

12221

11111

方法1:

四个拐角矩阵拼合而成。

方法1改进：

减少判断条件。

#include

main（）

{inti,j,k,n,mi,ma;

printf（"n:

"）;

scanf（"%d",&n）;

for（i=1;i<=n;i++）

{mi=i<=n+1-i?

i:

n+1-i;

ma=n+1-mi;

for（j=1;j<=n;j++）

{k=j

j:

ma

n+1-j:

mi;

printf（"%3d",k）;

}

putchar（'\n'）;

方法2：

利用对称性。

#include#defineN20voidmain（）{

inta[N][N]={0},i,j,Q,n;

printf（"n="）;scanf（"%d",&n）;

Q=n/2+1;

for（i=1;i<=Q;i++）

for（j=1;j<=Q;j++）

{if（i<=j）

a[i][j]=i;

else

a[i][j]=j;

a[i][n+1-j]=a[i][j];

a[n+1-i][j]=a[i][j];a[n+1-i][n+1-j]=a[i][j];

}

for（i=1;i<=n;i++）

{for（j=1;j<=n;j++）

printf（"%4d",a[i][j]）;

printf（"\n"）;

}

}

方法3：

按圈打。

#include

intmin（inta,intb,intc,intd）

{

intm=a;

if（m>b）m=b;

if（m>c）m=c;

if（m>d）m=d;

returnm;

}

main（）

{inti,j,k,n,mi,ma;printf（"n:

"）;scanf（"%d",&n）;for（i=1;i<=n;i++）

{for（j=1;j<=n;j++）

{k=min（i,j,n+1-i,n+1-j）;printf（"%4d",k）;

putchar（'\n'）;

}

5.螺旋矩阵

1

16

15

14

13

2

17

24

23

12

3

18

25

22

11

4

19

20

21

10

5

6

7

8

9

拟人法：

按圈行走#include#defineN20voidmain（）{

inta[N][N]={0};

intn,s,i,j,edge;printf（"n="）;scanf（"%d",&n）;edge=n,s=1;i=j=1;

do{

while（a[i][j]==0&&i<=edge）

{a[i][j]=s;

s++;i++;}

i--;j++;

while（a[i][j]==0&&j<=edge）

{a[i][j]=s;

s++;j++;}

j--;i--;

while（a[i][j]==0&&i>=n+1-edge）{a[i][j]=s;

s++;i--;}

i++;j--;

while（a[i][j]==0&&j>=n+1-edge）

{a[i][j]=s;

s++;j--;}

j++;i++;

}while（s<=n*n）;

for（i=1;i<=n;i++）

{for（j=1;j<=n;j++）printf（"%4d",a[i][j]）;

printf（"\n"）;

}

解析法：

按区域填空#includemain（）

{intn,i,j,k,s,d,l;

inta[20][20]={0};printf（"n:

"）;scanf（"%d",&n）;i=j=1;

for（k=1;k<=n*n;k++）

{a[i][j]=k;if（i+j=j-1）i++;elseif（i>j&&i+j>=n+1）j++;elseif（i+j>n+1&&i<=j）i--;elseif（i+j<=n+1&&i

}

for（i=1;i<=n;i++）

{for（j=1;j<=n;j++）printf（"%4d",a[i][j]）;

printf（"\n"）;

}

}解析法：

按圈、段，位置填空#include#defineN20voidmain（）

{staticinta[N][N];

inti,j,D,Q,G,n,k,m,s;printf（"n="）;

scanf（"%d",&n）;for（i=1;i<=n;i++）

for（j=1;j<=n;j++）

{

if（i>=j&&i+j

elseif（i+j>=n+1&&i>j）{D=2;Q=n+1-i;G=j-（Q-1）;}

elseif（i<=j&&i+j>n+1）{D=3;Q=n+1-j;G=n+1-i-（Q-1）;}

else{D=4;Q=i;G=n+1-j-（Q-1）;}

s=0;m=n-1;for（k=1;k<=Q-1;k++）s+=4*（m-2*（k-1））;

a[i][j]=s+（D-1）*（m-2*（Q-1））+G;

for（i=1;i<=n;i++）

{

for（j=1;j<=n;j++）

printf（"%4d",a[i][j]）;printf（"\n"）;

}

}

6.

斜行矩阵

1

2

4

7

11

3

5

8

12

16

6

9

13

17

20

1014182123

1519222425

#include

#defineN20voidmain（）

{staticinta[N][N];inti=1,j=1,n,k=1;printf（"n="）;scanf（"%d",&n）;a[1][1]=k;while（k++<=25）if（i==n）

{i=j+1;j=n;a[i][j]=k;}elseif（j==1）

{j=i+1;i=1;a[i][j]=k;}else

{i++;j--;a[i][j]=k;}for（i=1;i<=n;i++）

{for（j=1;j<=n;j++）printf（"%4d",a[i][j]）;

printf（"\n"）;

}

}

7.蛇形矩阵

1

2

6

7

15

3

5

8

14

16

4

9

13

17

22

10

12

18

21

23

11

19

20

24

25

#include

#defineN20

voidmain（）

{

staticinta[N][N];

inti,j,n,d,k;

printf（"n="）;

scanf（"%d",&n）;

i=j=1;d=1;

for（k=1;k<=n*n;k++）

{

a[i][j]=k;

i-=d;j+=d;

if（i==n+1）{i=n;j+=2;d=-d;}

elseif（j==n+1）{i+=2;j=n;d=-d;}

elseif（i==0）{i=1;d=-d;}

elseif（j==0）{j=1;d=-d;}

}

for（i=1;i<=n;i++）{for（j=1;j<=n;j++）

printf（"%4d",a[i][j]）;printf（"\n"）;

}}8.杨辉三角阵

1

11

121

1331

14641使用二维数组include

#defineN20voidmain（）{

staticinta[N][N];inti,j,n;

printf（"n="）;scanf（"%d",&n）;

a[0][0]=1;for（i=1;i<=n;i++）

for（j=1;j<=i;j++）a[i][j]=a[i-1][j-1]+a[i-1][j];

for（i=1;i<=n;i++）

{for（j=1;j<=i;j++）printf（"%4d",a[i][j]）;

printf（"\n"）;

}

}使用一维数组#include#defineN20voidmain（）

{

staticinta[N];

inti,j,n;printf（"n="）;scanf（"%d",&n）;

a[1]=1;

for（i=1;i<=n;i++）

{for（j=i;j>=1;j--）a[j]=a[j]+a[j-1];

for（j=1;j<=i;j++）printf（"%4d",a[j]）;

printf（"\n"）;

}

}

9.直角三角阵

1）形式1

1

2

4

7

3610

5914

813

12

15

拟人法：

11

#include

#defineN20

voidmain（）

{

staticinta[N][N];

inti=1,j=1,n,k=1;printf（"n="）;scanf（"%d",&n）;a[1][1]=1;

while（k++<=n*（n+1）/2）if（i==1）

{i=j+1;j=1;a[i][j]=k;}

else

{i--;j++;a[i][j]=k;}for（i=1;i<=n;i++）{for（j=1;i+j<=n+1;j++）printf（"%4d",a[i][j]）;printf（"\n"）;

}

}

解析法：

#include#defineN20voidmain（）

{

staticinta[N][N];

inti,j,n;printf（"n="）;scanf（"%d",&n）;for（i=1;i<=n;i++）for（j=1;j<=n+1-i;j++）if（i==1&&j==1）a[i][j]=1;

elseif（j==1）a[i][j]=a[i-1][1]+i-1;

elsea[i][j]=a[i][j-1]+j+（i-1）;

for（i=1;i<=n;i++）{for（j=1;j<=n;j++）printf（"%4d",a[i][j]）;

printf（"\n"）;

}

}解析法：

按层打印#include#defineN20voidmain（）

{

staticinta[N][N];

inti,j,n,L;printf（"n="）;scanf（"%d",&n）;for（i=1;i<=n;i++）for（j=1;j<=n+1-i;j++）{L=i+j-1;a[i][j]=L*（L-1）/2+1+j-1;

for（i=1;i<=n;i++）

{for（j=1;j<=n;j++）

printf（"%4d",a[i][j]）;

printf（"\n"）;

}

}

2）形式2

16101315

271114

3812

49

5

#include

#defineN20

voidmain（）

{

staticinta[N][N];

inti=1,j=1,n,k=1;

printf（"n="）;

scanf（"%d",&n）;

a[1][1]=1;

while（k++<=n*（n+1）/2）

if（i+j==n+1）

{j=n+1-i+1;i=1;a[i][j]=k;}

else

{i++;a[i][j]=k;}

for（i=1;i<=n;i++）

{for（j=1;i+j<=n+1;j++）

printf（"%4d",a[i][j]）;

printf（"\n"）;

}

}

3）形式3

1

26

3710

481113

59121415

#include

#defineN20

voidmain（）

staticinta[N][N];inti=1,j=1,n,k=1;printf（"n="）;scanf（"%d",&n）;a[1][1]=1;

while（k++<=n*（n+1）/2）if（i==n）

{i=j+1;j++;a[i][j]=k;}else

{i++;a[i][j]=k;}

for（i=1;i<=n;i++）

{for（j=1;j<=i;j++）

printf（"%4d",a[i][j]）;

printf（"\n"）;

}

}

4）形式4

1

6

2

10

7

3

13

11

84

15

14

1295

#include

#defineN20voidmain（）

{

staticinta[N][N];

inti=1,j=1,n,k=1;printf（"n="）;scanf（"%d",&n）;

a[1][1]=1;while（k++<=n*（n+1）/2）if（i==n）

{i=n+1-j+1;j=1;a[i][j]=k;}else

{i++;j++;a[i][j]=k;}for（i=1;i<=n;i++）

{for（j=1;j<=i;j++）printf（"%4d",a[i][j]）;

printf（"\n"）;

}

}

1.打印星号图。

1）

共打印3行，每列6个。

***

***

***

*

*

*

*

*

*

*

*

*

2）

平行四边形

*

*

*

*

**

*

*

***

*

****

3）

等腰三角形

*

**

*

***

*

*

****

*

*

*

4）

菱形

*

**

*

***

*

*

****

*

*

*

***

*

*

**

*

*

方法

2：

共7行，上

4行：

每i行先打印4-i个空格，再打印2i-1个‘*'号。

下3行：

行数递减时，每i行先打印4-i个空格，再打印2i-1个‘*'号。

对m行，n=m/2+1，先打印1~n行，再打印n-1~1行。

#includevoidmain（）{

inti,j,n,m;

printf（"inputm"）;

scanf（"%d",&m）;n=m/2+1;

for（i=1;i<=n;i++）

{for（j=1;j<=n-i;j++）putchar（''）;

for（j=1;j<=2*i-1;j++）putchar（'*'）;

printf（"\n"）;

}

for（i=n-1;i>0;i--）

{

for（j=1;j<=n-i;j++）putchar（''）;

for（j=1;j<=2*i-1;j++）putchar（'*'）;

printf（"\n"）;

}

}

方法3:

统一处理

#include

#include

voidmain（）

{

inti,j;

for（i=1;i<=7;i++）

{for（j=1;j<=abs（i-4）;j++）printf（""）;

for（j=1;j<=7-2*abs（i-4）;j++）

printf（"*"）;

printf（"\n"）;

}

}

5）

两个等腰三角形

*

*

**

*

***

***

**

*****

****

****

*****

6）

两个平行四边形

***

*

**

**

**

***

*

***

****

****

****

2.打印字母等腰三角形

1）

三角形的大小由键盘输入，如

n=5，如图

A

A

B

C

A

B

C

D

E

A

B

C

D

E

F

G

A

B

C

D

E

F

G

H

I

2）打印字母对称的等腰三角形，三角形大小由键盘输入。

如图

A

B

A

B

C

B

A

B

C

D

C

B

A

B

C

D

E

D

C

B

A

B

C

D

E

11副对角线及其下面i+j=n+1,a[i][j]=n+1-i