《算法设计与分析》上机实验报告5.docx

《算法设计与分析》上机实验报告5.docx

《《算法设计与分析》上机实验报告5.docx》由会员分享，可在线阅读，更多相关《《算法设计与分析》上机实验报告5.docx（12页珍藏版）》请在冰豆网上搜索。

《算法设计与分析》上机实验报告5

福州大学数学与计算机科学学院

《算法设计与分析》上机实验报告（5）

专业和班级

姓名

成绩

学号

实验名称

单源最短路径问题

实验目的和求

1. 理解算法设计的基本步骤和各步的主要内容，基本要求

2. 加深对分支限界法基本思想的理解

3.培养学生用计算机解决实际问题的能力

实验任务

1.掌握单源最短路径问题的基本算法及其应用 

2. 利用分支限界法找出具体问题的最优解

3. 分析实验结果，总结算法的时间和空间复杂度 

实验步骤

1.单源最短路径问题描述

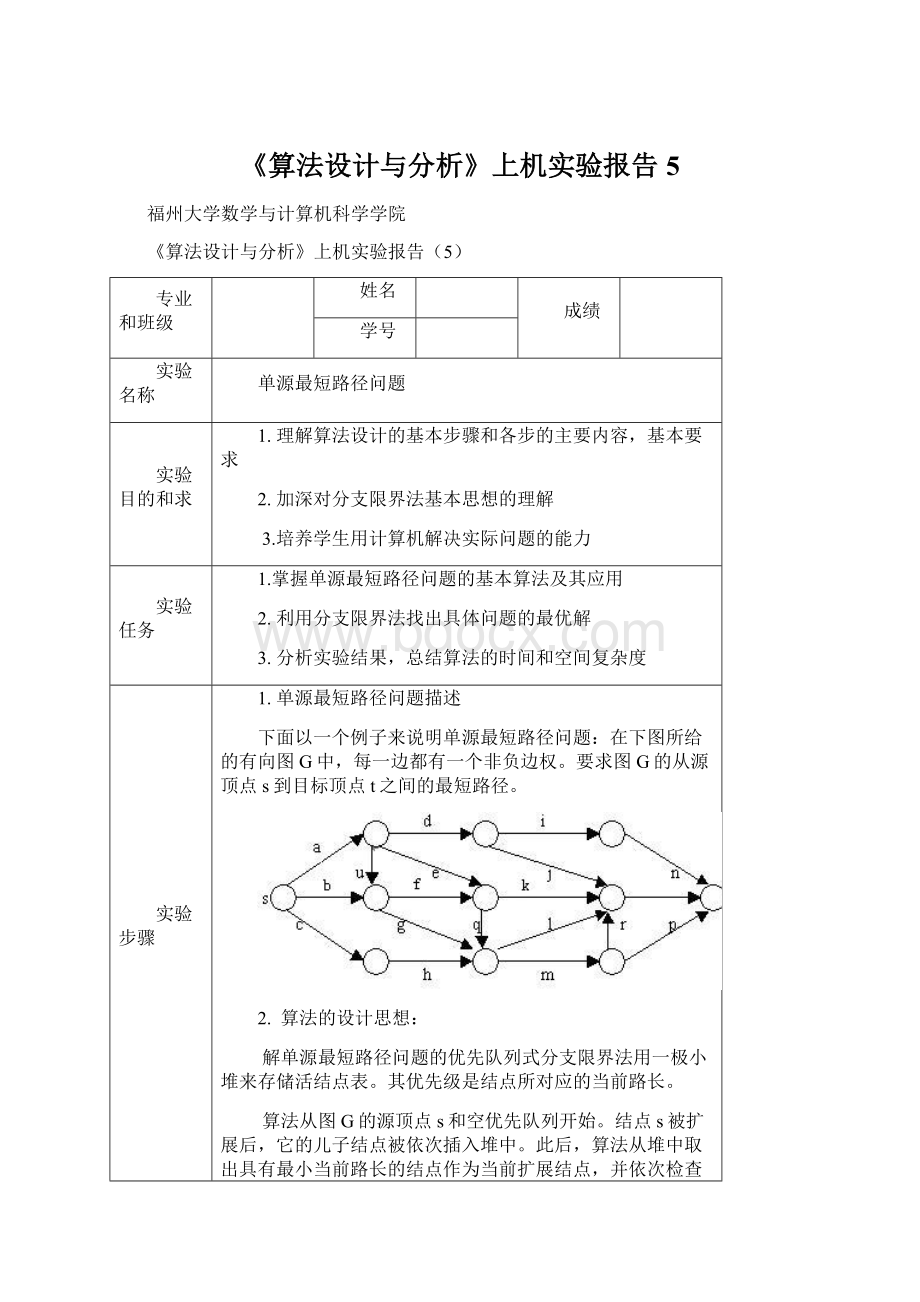
下面以一个例子来说明单源最短路径问题：

在下图所给的有向图G中，每一边都有一个非负边权。

要求图G的从源顶点s到目标顶点t之间的最短路径。

2.算法的设计思想：

解单源最短路径问题的优先队列式分支限界法用一极小堆来存储活结点表。

其优先级是结点所对应的当前路长。

算法从图G的源顶点s和空优先队列开始。

结点s被扩展后，它的儿子结点被依次插入堆中。

此后，算法从堆中取出具有最小当前路长的结点作为当前扩展结点，并依次检查与当前扩展结点相邻的所有顶点。

如果从当前扩展结点i到顶点j有边可达，且从源出发，途经顶点i再到顶点j的所相应的路径的长度小于当前最优路径长度，则将该顶点作为活结点插入到活结点优先队列中。

这个结点的扩展过程一直继续到活结点优先队列为空时为止。

3.剪枝策略

在算法扩展结点的过程中，一旦发现一个结点的下界不小于当前找到的最短路长，则算法剪去以该结点为根的子树。

在算法中，利用结点间的控制关系进行剪枝。

从源顶点s出发，2条不同路径到达图G的同一顶点。

由于两条路径的路长不同，因此可以将路长长的路径所对应的树中的结点为根的子树剪去。

4.单源最短路径问题程序代码

1、MinHeap2.h

1.#include   

2.  

3.template  

4.class Graph;  

5.  

6.template   

7.class MinHeap   

8.{   

9.    template  

10.    friend class Graph;  

11.    public:

12.        MinHeap（int maxheapsize = 10）;   

13.        ~MinHeap（）{delete []heap;}   

14.  

15.        int Size（） const{return currentsize;}   

16.        T Max（）{if（currentsize） return heap[1];}   

17.  

18.        MinHeap& Insert（const T& x）;   

19.        MinHeap& DeleteMin（T &x）;   

20.  

21.        void Initialize（T x[], int size, int ArraySize）;   

22.        void Deactivate（）;   

23.        void output（T a[],int n）;  

24.    private:

25.        int currentsize, maxsize;   

26.        T *heap;   

27.};   

28.  

29.template    

30.void MinHeap:

:

output（T a[],int n）   

31.{   

32.    for（int i = 1; i <= n; i++）   

33.    cout << a[i] << " ";   

34.    cout << endl;   

35.}   

36.  

37.template    

38.MinHeap:

:

MinHeap（int maxheapsize）   

39.{   

40.    maxsize = maxheapsize;   

41.    heap = new T[maxsize + 1];   

42.    currentsize = 0;   

43.}   

44.  

45.template   

46.MinHeap& MinHeap:

:

Insert（const T& x）   

47.{   

48.    if（currentsize == maxsize）   

49.    {   

50.        return *this;   

51.    }   

52.    int i = ++currentsize;   

53.    while（i !

= 1 && x < heap[i/2]）   

54.    {   

55.        heap[i] = heap[i/2];   

56.        i /= 2;   

57.    }   

58.  

59.    heap[i] = x;   

60.    return *this;   

61.}   

62.  

63.template   

64.MinHeap& MinHeap:

:

DeleteMin（T& x）   

65.{   

66.    if（currentsize == 0）   

67.    {   

68.        cout<<"Empty heap!

"<

69.        return *this;   

70.    }   

71.  

72.    x = heap[1];   

73.  

74.    T y = heap[currentsize--];   

75.    int i = 1, ci = 2;   

76.    while（ci <= currentsize）   

77.    {   

78.        if（ci < currentsize && heap[ci] > heap[ci + 1]）   

79.        {   

80.            ci++;   

81.        }   

82.  

83.        if（y <= heap[ci]）   

84.        {   

85.            break;   

86.        }   

87.        heap[i] = heap[ci];   

88.        i = ci;   

89.        ci *= 2;   

90.    }   

91.  

92.    heap[i] = y;   

93.    return *this;   

94.}   

95.  

96.template   

97.void MinHeap:

:

Initialize（T x[], int size, int ArraySize）   

98.{   

99.    delete []heap;   

100.    heap = x;   

101.    currentsize = size;   

102.    maxsize = ArraySize;   

103.  

104.    for（int i = currentsize / 2; i >= 1; i--）   

105.    {   

106.        T y = heap[i];   

107.        int c = 2 * i;   

108.        while（c <= currentsize）   

109.        {   

110.            if（c < currentsize && heap[c] > heap[c + 1]）   

111.                c++;   

112.            if（y <= heap[c]）   

113.                break;   

114.            heap[c / 2] = heap[c];   

115.            c *= 2;   

116.        }   

117.        heap[c / 2] = y;   

118.    }   

119.}   

120.  

121.template   

122.void MinHeap:

:

Deactivate（）   

123.{   

124.    heap = 0;   

125.}   

  2、zuiduanlujing.cpp

1.//单源最短路径问题 分支 限界法求解  

2.#include "stdafx.h"  

3.#include "MinHeap2.h"  

4.#include   

5.#include    

6.using namespace std;  

7.  

8.ifstream fin（"6d2.txt"）;   

9.  

10.template  

11.class Graph  

12.{  

13.    friend int main（）;  

14.    public:

15.        void ShortesPaths（int）;  

16.    private:

17.        int     n,         //图G的顶点数  

18.                *prev;     //前驱顶点数组  

19.        Type    **c,       //图G的领接矩阵  

20.                *dist;     //最短距离数组  

21.};   

22.  

23.template  

24.class MinHeapNode  

25.{  

26.   friend Graph;  

27.   public:

28.       operator int （）const{return length;}  

29.   private:

30.       int       i;       //顶点编号  

31.       Type  length;      //当前路长  

32.};   

33.  

34.template  

35.void Graph:

:

ShortesPaths（int v）//单源最短路径问题的优先队列式分支限界法  

36.{   

37.    MinHeap> H（1000）;  

38.    MinHeapNode E;  

39.  

40.    //定义源为初始扩展节点  

41.    E.i=v;  

42.    E.length=0;  

43.    dist[v]=0;  

44.  

45.    while （true）//搜索问题的解空间  

46.    {  

47.        for （int j = 1; j <= n; j++）  

48.            if （（c[E.i][j]!

=0）&&（E.length+c[E.i][j]

49.  

50.                 // 顶点i到顶点j可达，且满足控制约束  

51.                 dist[j]=E.length+c[E.i][j];  

52.                 prev[j]=E.i;  

53.  

54.                 // 加入活结点优先队列  

55.                 MinHeapNode N;  

56.                 N.i=j;  

57.                 N.length=dist[j];  

58.                 H.Insert（N）;  

59.            }`  

60.        try   

61.        {  

62.            H.DeleteMin（E）; // 取下一扩展结点  

63.        }          

64.        catch （int）   

65.        {  

66.            break;  

67.        }    

68.        if （H.currentsize==0）// 优先队列空  

69.        {  

70.            break;  

71.        }  

72.    }  

73.}  

74.  

75.int main（）  

76.{    

77.    int n=11;  

78.    int prev[12] = {0,0,0,0,0,0,0,0,0,0,0,0};    

79.  

80.    int dist[12]={1000,1000,1000,1000,1000,1000,1000,1000,1000,1000,1000,1000};  

81.  

82.    cout<<"单源图的邻接矩阵如下：

"<

83.    int **c = new int*[n+1];  

84.  

85.    for（int i=1;i<=n;i++）  

86.    {  

87.        c[i]=new int[n+1];  

88.        for（int j=1; j<=n; j++）  

89.        {  

90.            fin>>c[i][j];  

91.            cout<

92.        }  

93.        cout<

94.    }  

95.  

96.    int v=1;  

97.    Graph G;  

98.    G.n=n;  

99.  

100.    G.c=c;  

101.    G.dist=dist;  

102.    G.prev=prev;  

103.    G.ShortesPaths（v）;  

104.  

105.    cout<<"从S到T的最短路长是：

"<

106.    for （int i = 2; i <= n; i++）  

107.    {  

108.        cout<<"prev（"<

109.    }  

110.  

111.    for （int i = 2; i <= n; i++）  

112.    {  

113.        cout<<"从1到"<

"<

114.    }  

115.  

116.    for（int i=1;i<=n;i++）  

117.    {  

118.        delete []c[i];  

119.    }  

120.  

121.    delete []c;  

122.    c=0;      

123.    return 0;  

124.}  

实验结果

通过上面的结果图可以看出程序能够快速求出单源最短路径问题的最优解.