北京高考数学理科含答案.docx

北京高考数学理科含答案.docx

《北京高考数学理科含答案.docx》由会员分享，可在线阅读，更多相关《北京高考数学理科含答案.docx（13页珍藏版）》请在冰豆网上搜索。

北京高考数学理科含答案

2014年北京高考数学（理科）试题

1•已知集合A{x|x2

2x0},B{0,1,2}，则AI

B（）

A.{0}B.{0,1}

C.{0,2}D.{0,1,2}

2•下列函数中，在区间

（0,）上为增函数的是（

）

A.y.x1B.y

2x

（x1）2C.y2

D.yiog0.5（x■

x1cos

3•曲线

y2sin

（为参数）的对称中心（

）

A.在直线y2x上

B.在直线y2x上

C.在直线yx1上

D.在直线yx1上

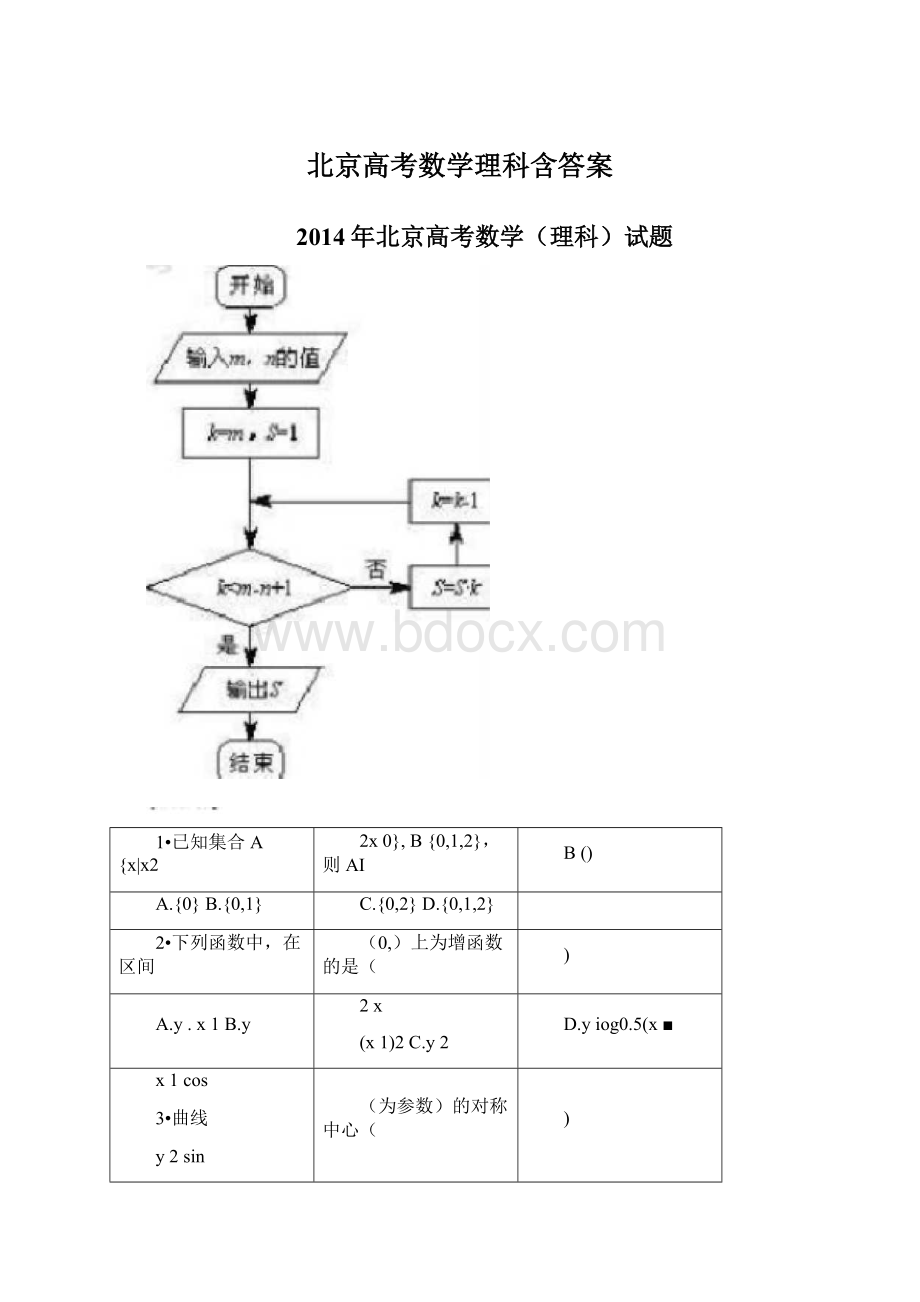
4.当m7,n3时，执行如图所示的程序框图，输出的

S值为（）

.选择题（共8小题，每小题5分，共40分•在每小题列出的四个选项中，选出符合题目要求的一项）

1）

A.7B.42C.210D.840

5•设{an}是公比为q的等比数列，贝y"q1"是"{an}"为递增数列的（）

A.充分且不必要条件

B.必要且不充分条件

C.充分必要条件

D.既不充分也不必要条件

xy

2

0

6•若x,y满足kxy

2

0且zyx的最小值为-4，则k的值为（

）

y

0

A.2B.2C.

1

D.丄

2

2

7•在空间直角坐标系Oxyz中，已知A2,0,0,B2,2,0,C0,2,0,D1,1,、、2，若

Si,S2,S3分别表示三棱锥DABC在xOy,yOz,zOx坐标平面上的正投影图形的

面积，则（）

（B）SiS2且S3S|

（C）SiS3且S3S2

（D）S2S3且SiS3

（A）SiS2S3

8•有语文、数学两学科，成绩评定为“优秀”“合格”“不合格”三种.若A同学每科成绩不

低于B同学，且至少有一科成绩比B高，则称“A同学比B同学成绩好•”现有若干同学,他们之间没有一个人比另一个成绩好，且没有任意两个人语文成绩一样，数学成绩也一样的•问满足条件的最多有多少学生（）

（a）2

（B）3

（C）4

（D）5

二、填空题

（共

6小题，每小题5分

卜，共

30分）

1

9.复数—

2

i

1

i

r

r

■r

rr

10.已知向量

a、

b满足c

a1，b

2,1

，且ab0

R，则

y22

11.设双曲线C经过点2,2，且与匚x1具有相同渐近线，则C的方程为；

4

渐近线方程为.

12.若等差数列an满足a7a8a?

0，a?

ai°0,则当n时a“的前n

项和最大.

13.把5件不同产品摆成一排，若产品

A与产品C不相邻，则不同的摆法有

14.设函数f（x）sin（x），A0,

0,若f（x）在学科网区间［―,—］上具有单调性，且

62

，则f（x）的最小正周期为

6

三•解答题（共6题，满分80分）

1

15.（本小题13分）如图，在ABC中，B-,AB8，点D在BC边上，且CD2,cosADC-37

（1）求sinBAD

（2）求BD,AC的长

16.（本小题13分）.

李明在10场篮球比赛中的投篮情况如下（假设各场比赛互相独立）

场次

投篮次数

命中次数

场次

投篮次数

命中次数

主场1

22

12

客场1

18

8

主场2

15

12

客场2

13

12

主场3

12

8

客场3

21

7

主场4

23

8

客场4

18

15

主场5

24

20

客场5

25

12

（1）从上述比赛中随机选择一场，求李明在该场比赛中投篮命中率超过0.6的概率•

（2）从上述比赛中选择一个主场和一个客场，求李明的投篮命中率一场超过0.6，一

场不超过0.6的概率•

（3）记X是表中10个命中次数的平均数，从上述比赛中随机选择一场，记X为李明

在这比赛中的命中次数，比较E（X）与x的大小学科网（只需写出结论）

17.（本小题14分）

如图，正方形AMDE的边长为2，B,C分别为AM,MD的中点，在五棱锥PABCDE

中，F为棱PE的中点，平面ABF与棱PD,PC分别交于点G,H.

1）求证：

AB//FG；

（2）若PA底面ABCDE，且AFPE，求直线BC与平面ABF所成角的大小，并求线段PH的长.

18.（本小题13分）

已知函数f（x）xcosxsinx,x[0,—],

2

（1）求证：

f（x）0；

sinx

（2）若ab在（0,—）上恒成立，求a的最大值与b的最小值.

x2

19.（本小题14分）

22

2

y22的

已知椭圆C:

x22y24，

（1）求椭圆C的离心率.

（2）设0为原点，若点A在椭圆C上，点B在直线y2上，且OAOB，求直线AB与圆x2位置关系，并证明你的结论.

20.（本小题13分）对于数对序列P（a1,b1）,（a2,b2）,L,（an,bn），记T1（P）a1b1，

Tk（P）bkmax{Tki（P）,aia?

Lak}（2kn），其中

max{Tki（P）,sia?

Lak}表示Tki（P）和印a?

Lak两个数中最大的数，

（1）对于数对序列P（2,5）,P（4,1），求T1（P）,T2（P）的值.

（2）记m为a,b,c,d四个数中最小值，对于由两个数对（a,b）,（c,d）组成的数对序列P（a,b）,（c,d）和

P'（a,b）,（c,d），试分别对ma和md的两种情况比较T2（P）和T2（P'）的大小.

（3）在由5个数对（11,8）,（5,2）,（16,11）,（11,11）,（4,6）组成的所有数对序列中，写出一个数对序列P使Ts（P）最小，并写出T5（P）的值.（只需写出结论）.

2014年普通高等学校招生全国统一考试

数学（理）（北京卷）参考答案

、选择题（共

8小题，每小题5分，共40分）

（1）C

（2）A（3）B（4）C

（5）D

（6）D（7）D（8）B

二、填空题

（共6小题,

每小题

5分,

共30分）

（9）1

（10）

5

2

2

x

y

（11）

1

y

2x

（12）8

3

12

（13）36（14）

三、解答题（共6小题，共80分）

（15）（共13分）

解：

（I）在ADC中，因为COSADC

丄，所以sinADC口

77

所以sinBADsin（ADCB）

sinADCcosBcosADCsinB

4.3丄1丄33\3

727214

（u）在ABD中，由正弦定理得

BD

ABsinBAD

sinADB

14

4、3

在ABC中，由余弦定理得

AC

22

ABBC2ABBCcosB

8252285-49

2

所以AC7

（16）

解（I）根据投篮计数据可以算岀李明投篮命中率超过0.6的场次有5场，

分别是主场2，主场3，主场5，客场2,客场4.

所以在随机选择的一场比赛中，李明的投篮命中率超过0.6的概率是0.5.

（H）设事件A为“在随机选择的一场主场比赛中李明的投篮命中率超过0.6”，

事件B为“在随机选择的一场客场比赛中李明的投篮命中率超过0.6”，

事件C为“在随机选择的一个主场和一个客场中，李明的投篮命中率一场超过0.6，—场不超过0.6”。

则C=ABUAB，a,b独立。

32

根据投篮统计数据，P（A）—，P（B）—.

55

P（C）P（AB）P（AB）

3322

5555

13

25

13

所以，在随机选择的一个主场和一个客场中，李明的投篮命中率一场超过0.6，—场不超过0.6的概率为.

25

（山）EXX.

（17）（共14分）

解：

（I）在正方形中，因为B是am的中点，所以AB//DE。

又因为AB平面PDE

所以AB/平面PDE

因为AB平面abf,且平面ABFI平面PDFFG,

所以AB//FG。

（n）因为PA底面ABCDE所以PAAB,PAAE.

如图建立空间直角坐标系Axyz，则A（0,0,0）,B（1,0,0）,C（2,1,0）,P（0,0,2）,F（0,1,1）,

uuu

BC（1,1,0）.

设平面ABF的法向量为n（x,y,z），则

uuu

n

AB

0,

x

0,

uuir

即

n

AF

0,

y

z0.

uuu

令z

1,,

则y

1

。

所以n（0,1,1），设直线BC与平面ABF所成角为a,则sina

cos（n,BC）

nBC―；-uuur

nBC

因此直线BC与平面ABF所成角为30°.

设点H的坐标为（u,v,w）.

uuiruuu

因为点h在棱pc上，所以可设PHPC（0pp1）,,

即（u,v,w2）（2,1,2）.。

所以u2,v,w22

uuu

因为n是平面ABF的法向量，所以nAB0,即（0,1,1）（2,,22）0。

2422

解得，所以点聊坐标为©打.。

所以pH；（3）2（；）2（3）22

（18）（共13分）解：

（I）由f（x）xcosxsinx得

f'（x）cosxxsinxcosxxsinx。

因为在区间（0,—）上f'（x）

2

xsinxp0，所以f（x）在区间

0,—上单调递减

2

从而f（x）f（0）0

（u）当xf0时，“s^nxfa

x

等价于“sinxaxf0

等价于

sinxbxp0

令g（x）sinxcx，贝Ug'（x）cosxc,

当c0时，g（x）f0对任意x（0,—）恒成立。

2

当c1时，因为对任意x（0-），g'（x）

cosx

cp0，所以g（x）在区间

上单调递减

从而

g（x）pg（0）0对任意x（0,3）恒成立。

当0pcp1时，存在唯一的x0（0,3）使得g'（x0）cosxoc0。

g（x）与g'（x）在区间（0,—）上的情况如下：

2

x

（0,x0）

X。

（旳）

g'（x）

—

0

—

g（x）

/

因为g（x）在区间0,x0上是增函数，所以g（x0）fg（0）0。

进一步，“g（x）f0对

2

任意x（0,—）恒成立"当且仅当g（—）1c0，即0pc

222

2

综上所述，当且仅当c时，g（x）f0对任意x（0,—）恒成立；当且仅当c1时,

2

g（x）p0对任意x（0,）恒成立。

2

sinx2

所以，若appb对任意x（0,3）恒成立，则a最大值为，b的最小值为1.

（19）

解：

（I）由题意，椭圆

C的标准方程为

2

y-1。

2

所以a24,b2

2

2，从而c

b22。

因此a2,c、2

故椭圆c的离心率e

■1

2

（n）直线ab与圆

2相切。

证明如下:

设点A,B的坐标分别为

（X。

，y°），

（t,2），其中Xo0。

uuuuuu

因为OAOB，所以OAOB

0，即tXo2yo0，解得t

2y°

X0

当X0t时，y°f，代入椭圆

2

C的方程，得t.2，

故直线ab的方程为x

、、2。

圆心O到直线AB的距离d、.-。

此时直线AB与圆x2

2

y2相切。

当x0t时，直线AB的方程为y2

彰'（xt），

Xo

即（y°2）x（x°t）y2x°ty°

圆心0到直线AB的距离

2x0ty0

t）2

又X022y024，t

2

纽故

此时直线AB与圆x2

2相切。

20）

解：

（I）T1（P）

25

7

T1（P）

1maxT1（P）,241

max

7,6=8

（u）T2（P）maxa

bd,ac

d

T2（P'）

maxc

db,ca

b.

当m=a时，

T2（P'）=

maxcd

b,cab

=cdb

因为cd

bc

bd，且a

cd

c

bd，所以T2（P）

当m=d时，

T2（P'）

maxcd

b,c

ab

cab

因为ab

d

ab，且a

cd

c

ab所以T2（P）

所以无论m=a还是m=dT2（P）

（山）数对序列P：

（4,6）,（11,11）,（16,11）,（11,8）,（5,2）的T5（P）值最小,

T1（P）=10，T2（P）=26，T3（P）=42，T4（P）=50，T5（P）=52