贵州大学机械原理教案第九章2.docx

贵州大学机械原理教案第九章2.docx

《贵州大学机械原理教案第九章2.docx》由会员分享，可在线阅读，更多相关《贵州大学机械原理教案第九章2.docx（16页珍藏版）》请在冰豆网上搜索。

贵州大学机械原理教案第九章2

贵州大学教案

课程名称：

机械原理

授课教师

***

所在单位

机械基础教研室

课程类别

课堂理论教学

授课时间

06～07学年1学期11周

周一第2大节，2学时

授课内容

第九章凸轮机构及其设计

授课对象

机械学院XXXX班、选课156人

教学内容提要

 第三节　凸轮轮廓曲线的设计

当根据使用场合和工作要求选定了凸轮机构的类型和从动件的运动规律后，即可根据选定的基圆半径着手进行凸轮轮廓曲线的设计。

   凸轮廓线的设计方法有作图法和解析法，其依据的基本原理相同。

本节首先介绍凸轮廓线设计的基本原理，然后分别介绍作图法和解析法设计凸轮廓线的方法和步骤。

 　1.凸轮廓线设计方法的基本原理

凸轮机构工作时，凸轮和从动件都在运动，为了在图纸上绘制出凸轮的轮廓曲线，可采用反转法。

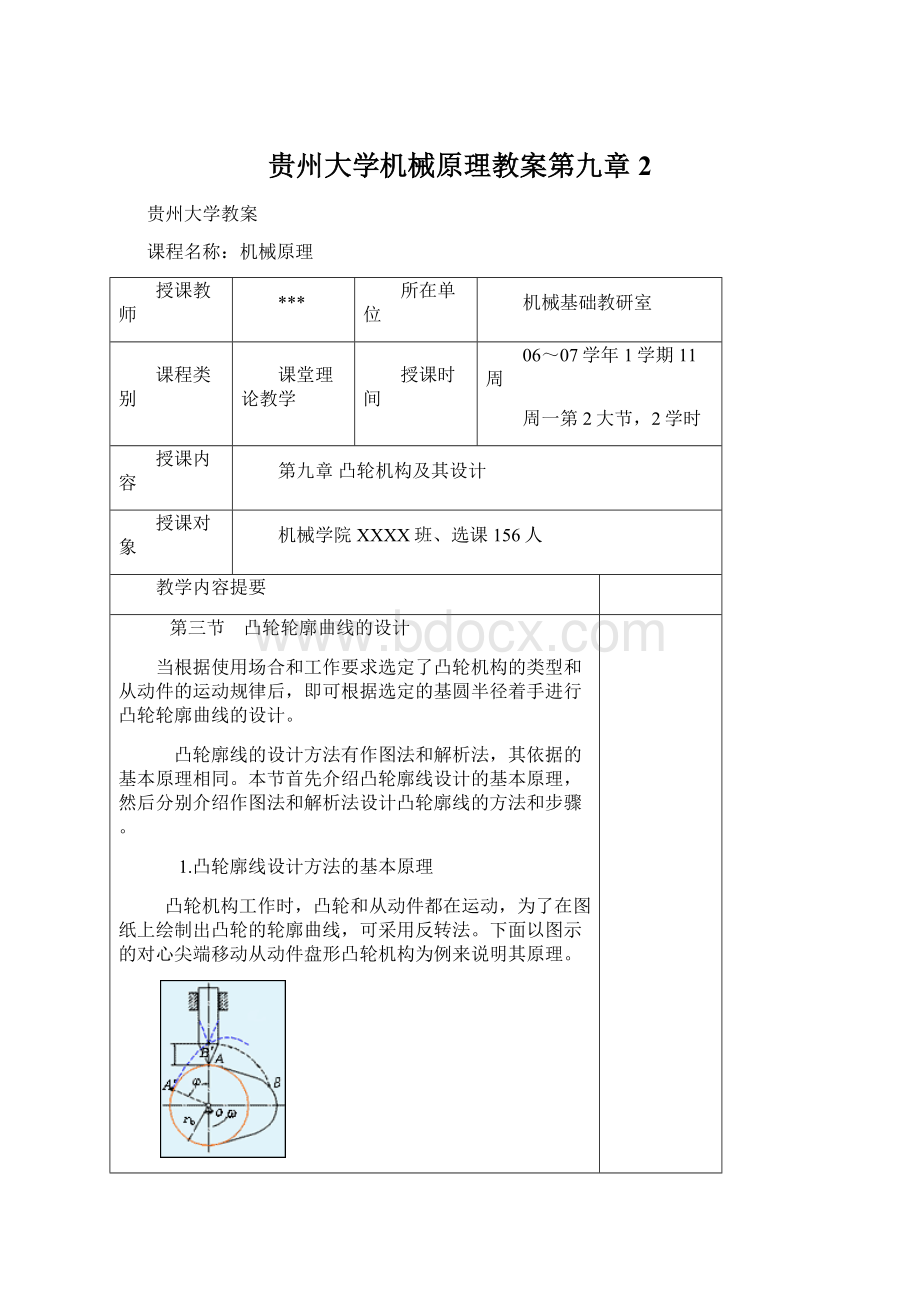
下面以图示的对心尖端移动从动件盘形凸轮机构为例来说明其原理。

真实运动反转过程

真实运动：

凸轮以等角速度ω绕轴O逆时针转动，推动从动件在导路中上、下往复移动。

无论是采用作图法还是解析法设计凸轮轮廓曲线，所依据的基本原理都是反转法原理。

　　根据上述分析，在设计凸轮廓线时，可假设凸轮静止不动，而使推杆相对于凸轮作反转运动；同时又在其导轨内作预期运动，作出推杆在这种复合运动中的一系列位置，则其尖顶的轨迹就是所要求的凸轮廓线。

这就是凸轮廓线设计方法的反转法原理。

教学内容提要

2.用作图法设计凸轮廓线

下面我们来介绍运用反转法原理设计凸轮廓线的具体作法。

（1）直动推杆盘形凸轮机构

　　在设计凸轮的轮廓时，需先取适当的比例尺μ1，根据已知的基圆半径r0和偏距e作出基圆和偏距圆，然后才能运用上述反转法进行作图。

其作图方法及步骤：

   a）选取适当的比例尺，作出从动件的位移线图。

将位移曲线的横坐标分成若干等份，得分点1，2,…，12。

   b）选取同样的比例尺，以O为圆心，rb为半径作基圆，并根据从动件的偏置方向画出从动件的起始位置线，该位置线与基圆的交点B0，便是从动件尖端的初始位置。

c）以O为圆心、OK＝e为半径作偏距圆，该圆与从动件的起始位置线切于K点。

  d）自K点开始，沿（-ω）方向将偏距圆分成与图（b）横坐标对应的区间和等份，得若干个分点。

过各分点作偏距圆的切射线，这些线代表从动件在反转过程中从动件占据的位置线。

它们与基圆的交点分别为C1，C2，…，C11。

   e）在上述切射线上，从基圆起向外截取线段，使其分别等于图（b）中相应的坐标，即C1B1＝11'，C2B2＝22',…,得点B1，B2，…，B11，这些点即代表反转过程中从动件尖端依次占据的位置。

   f）将点B0，B1，B2，…连成光滑的曲线，即得所求的凸轮轮廓曲线。

教学内容提要

对于偏置直动尖顶推杆盘形凸轮机构，推杆在反转运动中占据的各个位置为过基圆上各分点所作偏距圆的切线；而对于对心直动尖顶推杆盘形凸轮机构，可以认为是e=0时的偏置凸轮机构，则需过基圆上各分点作过凸轮回转中心的径向线即可，其他设计方法基本相同。

对于直动滚子推杆盘形凸轮机构，在设计凸轮廓线时，可首先将滚子中心视为尖顶推杆的尖顶，按前述方法定出滚子中心在推杆复合运动中的轨迹（称为凸轮的理论廓线），然后以理论廓线上一系列点为圆心，以滚子半径rr为半径作一系列的圆，再作此圆族的包络线，即为凸轮的工作廓线（又称实际廓线）。

值得注意，凸轮的基圆半径系指理论廓线的最小半径。

教学内容提要

对于直动平底推杆盘形凸轮机构，在设计这种凸轮廓线时，可将推杆导路中心线与推杆平底的交点A视为尖顶推杆的尖顶，按前述作图步骤确定出A在推杆复合运动中依次占据的各位置。

然后再过这些点作一系列代表推杆平底的直线，此直线族的包络线，即为凸轮的工作廓线。

（2）摆动推杆盘形凸轮机构

　　对于摆动尖顶推杆盘形凸轮机构凸轮廓线的设计，同样也可参照前述方法进行。

所不同的是推杆的预期运动规律要用推杆的角位移来表示，即在前面所得的直动推杆的各位移方程中，只需将位移s改为角位移φ；行程h改为角行程Φ，就可用来求摆动推杆的角位移了。

摆动平底推杆盘形凸轮机构的凸轮廓线设计（略）

摆动滚子推杆盘形凸轮机构的凸轮廓线设计（略）

（3）直动推杆圆柱凸轮机构

　　对于直动推杆圆柱凸轮机构，可设想将此圆柱凸轮的外表面展开在平面上，则得到一个移动速度为V（V＝Rω）的移动凸轮。

利用反转法原理，给整个移动凸轮机构加上一公共线速度—V后，此时凸轮将静止不动，推杆在随其导轨反向移动和在导轨中按预期的运动规律往复移动的复合运动时，其尖顶（或滚子中心或推杆导路中心线与推杆平底的交点A）描出的轨迹即为凸轮的理论廓线。

教学内容提要

　然后再用前述同样的方法就可求得移动凸轮的工作廓线。

最后，将这样作出的移动凸轮图卷于以只为半径的圆柱体上，并将其上的曲线描在圆柱体的表面上，即为所求的圆柱凸轮的轮廓曲线。

1．反转法原理

无论是用图解法还是解析法设计凸轮廓线，所依据的基本原理都是反转法原理。

   该原理可归纳如下：

   在凸轮机构中，如果对整个机构绕凸轮转动轴心O加上一个与凸轮转动角速度ω大小相等、方向相反的公共角速度（-ω），这时凸轮与从动件之间的相对运动关系并不改变。

但此时凸轮将固定不动，而移动从动件将一方面随导路一起以等角速度（-ω）绕O点转动，同时又按已知的运动规律在导路中作往复移动；摆动从动件将一方面随其摆动中心一起以等角速度（-ω）绕O点转动，同时又按已知的运动规律绕其摆动中心摆动，由于从动件尖端应始终与凸轮廓线相接触，故反转后从动件尖端相对于凸轮的运动轨迹，就是凸轮的轮廓曲线。

凸轮机构的型式多种多样，反转法原理适用于各种凸轮廓线的设计。

读者应在熟知反转法原理的基础上，结合教材认真复习，熟练掌握。

2．设计中易出现的错误

1）凸轮转角的分度；2）从动件位移量的量取；3）理论廓线与实际廓线

教学内容提要

3．反转法的灵活运用

凸轮廓线设计的反转法原理是本章的重点内容，通过以下几方面的练习灵活运用这一原理。

 1）已知从动件的运动规律，能熟练地运用反转法原理绘制出凸轮廓线。

 2）已知凸轮廓线，能熟练地运用反转法原理反求出从动件运动规律的位移曲线。

 3）已知凸轮廓线，能熟练地运用反转法原理求出凸轮从图示位置转过某一给定角度时，从动件走过的位移量、机构压力角。

 4）已知凸轮廓线，能熟练地运用反转法原理求当凸轮与从动件从某一点接触到另一点接触时，凸轮转过的角度。

2.用解析法设计凸轮廓线

 ●理论廓线方程   

所谓用解析法设计凸轮廓线，就是根据工作所要求的从动件的运动规律和已知的机构参数，求出凸轮廓线的方程式，并精确地计算出凸轮廓线上各点的坐标值。

图示为一偏置移动滚子从动件盘形凸轮机构。

选取直角坐标系xOy如图所示。

图中，B0点为从动件处于起始位置时滚子中心所处的位置；当凸轮转过φ角后，从动件的位移为s。

根据反转法原理作图，由图中可以看出，此时滚子中心将处于B点，该点的直角坐标为

式中，e为偏距；

。

式（3.1）即为凸轮理论廓线的方程式。

若为对心移动从动件，由于e =0，s0=rb,故上式可写成

教学内容提要

●实际廓线方程

在滚子从动件盘形凸轮机构中，凸轮的实际廓线是以理论廓线上各点为圆心，作一系列滚子圆，然后作该圆族的包络线得到的。

因此，实际廓线与理论廓线在法线方向上处处等距，该距离均等于滚子半径rr。

所以，如果已知理论廓线上任一点B的坐标（x,y）时，只要沿理论廓线在该点的法线方向取距离为rr，即可得到实际廓线上相应点B'的坐标值（x',y'）。

   由高等数学可知，曲线上任一点的法线斜率与该点的切线斜率互为负倒数，故理论廓线上B点处的法线nn的斜率为

由上图可以看出，当β求出后，实际廓线上对应点B'的坐标可由下式求出：

式中cosβ,sinβ可由式（3.3）求出，即有

将上两表达式代入式（3.4）可得

此即凸轮实际廓线的方程式。

式中，上面一组加减号表示一条内包络廓线η'，下面一组加减号表示一条外包络线η"。

教学内容提要

●刀具中心轨迹方程

   当在数控铣床上铣削凸轮或在凸轮磨床上磨削凸轮时，通常需要给出刀具中心的直角坐标值。

对于滚子从动件盘形凸轮，通常尽可能采用直径和滚子相同的刀具。

这时，刀具中心轨迹与凸轮理论廓线重合，理论廓线的方程即为刀具中心轨迹方程。

所以，在凸轮工作图上只需标注或附有理论廓线和实际廓线的坐标值，以供加工与检验时使用。

如果在机床上采用直径大于滚子的铣刀或砂轮来加工凸轮廓线，或在线切割机床上采用钼丝（直径远小于滚子）来加工凸轮廓线时，刀具中心将不在理论廓线上，所以还需要在凸轮工作图上标注或附有刀具中心轨迹的坐标值，以供加工时使用。

由上图（a）可看出，当刀具半径rc大于滚子半径rr时，刀具中心的运动轨迹ηc为凸轮理论廓线η的等距曲线。

它相当于以η上各点为圆心、以（rc－rr）为半径所作一系列滚子圆的外包络线。

由图（b）可看出，当刀具半径rc小于滚子半径时，刀具中心的运动轨迹ηc相当于以理论廓线η上各点为圆心、以（rr－rc）为半径所作的一系列滚子圆的内包络线。

因此，只要用|rc－rr|代替rr，便可由式（3.5）得到刀具中心轨迹方程

当rc＞rr时，取下面一组加减号；当rc＜rr时，取上面一组加减号。

教学内容提要

  2．对心平底推杆盘形凸轮机构

取平底与推杆的运动方向相同，偏距e=0（此种机构，e对推杆的运动规律无影响）

3．摆动滚子推杆盘形凸轮机构

教学内容提要

  第四节凸轮机构基本尺寸的确定

无论是用作图法还是解析法，在设计凸轮廓线前，除了需要根据工作要求选定从动件的运动规律外,还需确定凸轮机构的一些基本参数，如基圆半径rb、偏距e、滚子半径rr等。

这些参数的选择除应保证使从动件能准确地实现预期的运动规律外，还应使机构具有良好的受力状况和紧凑的尺寸。

1.凸轮机构中的作用力和凸轮机构的压力角

压力角是衡量凸轮机构传力特性好坏的一个重要参数。

   压力角定义：

在不计摩擦的情况下，凸轮对从动件作用力的方向线与从动件上力作用点的速度方向之间所夹的锐角。

如图所示的移动滚子从动件盘形凸轮机构，过滚子中心所作理论廓线的法线nn与从动件的运动方向线之间的夹角α就是其压力角。

在凸轮机构中，压力角α是影响凸轮机构受力情况的一个重要参数。

在其他条件相同的情况下，压力角愈大，则作用力F将愈大；如果压力角大到使作用力将增至无穷大时，机构将发生自锁，而此时的压力角特称为临界压力角αc，即

αc＝arctan{1/[（1+2b/l）tanφ2]}-φ1

为保证凸轮机构能正常运转，应使其最大压力角αmax小于临界压力角αc。

在生产实际中，为了提高机构的效率、改善其受力情况，通常规定凸轮机构的最大压力角αmax应小于某一许用压力角[α]。

其值一般为：

　　对直动推杆取[α]＝300；

　　对摆动推杆取[α]＝350～450；

　　回程时通常取[α]＝700～800。

2.凸轮基圆半径的确定

对于一定型式的凸轮机构，在推杆的运动规律选定后，该凸轮机构的压力角与凸轮基圆半径的大小直接相关。

教学内容提要

由此可知，在偏距一定，推杆的运动规律已知的条件下，加大基圆半径r。

，可减小压力角α，从而改善机

r0≥

构的传力特性。

但此时机构的尺寸将会增大。

故凸轮基圆半径的确定的原则

为：

在满足αmax≤[α]的条件下，合理地确定凸轮的基圆半径，使凸轮机构的尺寸不至过大。

　　在实际设计工作中，凸轮的基圆半径r。

的确定，不仅要受到αmax≤[α]的限制，还要考虑到凸轮的结构及强度的要求等。

因此在实际设计工作中，凸轮的基圆半径常是根据具体结构条件来选择的。

（例如：

取轴径的1.5—2倍），必要时再检查所设计的凸轮是否满足αmax≤[α]的要求。

　3.滚子推杆滚子半径的选择

滚子从动件盘形凸轮的实际廓线，是以理论廓线上各点为圆心作一系列滚子圆，然后作该圆族的包络线得到的。

因此，凸轮实际廓线的形状将受滚子半径大小的影响。

若滚子半径选择不当，有时可能使从动件不能准确地实现预期的运动规律。

设：

ρa—实际廓线的曲率半径；ρ--理论廓线的曲率半径；rr—滚子半径；

教学内容提要

  1）对于凸轮内凹：

ρa=ρ+rrr（实际廓线总可以作出）

2）对于凸轮外凸：

ρa=ρ-rr

ρ>rrρa>0实际廓线可以作出

ρ=rrρa=0实际廓线变尖

ρ

凸轮工作廓线的最小曲率半径ρamin一般不应小于1～5mm。

如果不能满足此要求时，就应增大基圆半径或适当减小滚子半径；有时必须修改推杆的运动规律，使凸轮工作廓线上出现尖点的地方代以合适的曲线。

通常取滚子半径rr=（0.1～0.5）r0。

（rr≤0.8ρmin）

●基圆半径的选择是一个既重要又复杂的问题：

   为了得到轻便紧凑的凸轮机构，希望基圆半径尽可能的小；但基圆半径过小，又可能造成运动失真和压力角超过许用值。

前者会使从动件不能实现预期的运动规律，后者会增大凸轮的推力和引起自锁。

因此：

   基圆半径的选取原则是：

在保证不产生运动失真和压力角不超过许用值的前提下，寻求最小的基圆半径。

为了减小凸轮的尺寸、重量和高速转动时的不平衡，希望有尽可能小的基圆半径。

移动滚子从动件盘形凸轮机构凸轮的最小基圆半径，主要受三个条件的限制，即：

1）凸轮的基圆半径应大于凸轮的凸轮轴的半径；

2）保证最大压力角αmax不超过许用压力角[α]；

3）保证凸轮实际廊线的最小曲率半径ρamin=ρmin-rr≥3-5mm，以避免运动失真和应力集中。

 在设计时，可根椐其中某限制条件确定最小基圆半径，然后用其它两个限制条件来校核。

例如，当用图解法设计凸轮时，可把根椐凸轮轴的直径或其它结构条件，凭经初选基圆半径通常取rb>（1.6~2）凸轮轴半径），待凸轮廓线设计时，可把根椐凸轮轴的直径或其它结构条件所选的基圆半径作为初值，而把压力角和曲率半径作为约束条件来处理。

    对于移动滚子从动件盘形凸轮机构，在设计凸轮廓线前，还需要确定滚子半径。

滚子半径选的过小，不能满足其结构和强度等方面的要求；滚子半径选的过大，又可能造成凸轮廓外凸部分产生失真。

通常在设计时，可先根椐和强度等方面的要求选择滚子半径，若凸轮廓线设计中出现运动失真，则可通过增大基圆半径解决。

教学内容提要

  4.平底推杆平底尺寸的确定

在设计平底从动件盘形凸轮机构时，为了保证机构在运转过程中，从动件平底与凸轮廓线始终正常接触，还必须确定平底的宽度。

由式前面公式可知，在任一瞬时，凸轮与平底的接触点偏离凸轮轴心的距离为ds/dδ。

因此，

平底尺寸：

l=2lmax+（5～7）mm

对于平底推杆凸轮机构，当凸轮的工作廓线不能与平底的位置线相切时，推杆将不能按预期的运动规律运动，即出现失真现象。

为了解决这个问题，可适当增大凸轮的基圆半径避免失真现象。

下图为一移动平底从动件盘形凸轮机构的设计图。

所选用的基圆半径rb=25mm，从动件运动规律为：

当凸轮转过90°时，从动件以摆线运动规律上升h=100mm；当凸轮转过一周中剩余270°时，从动件以摆线运动规律返回原处。

从图中可以明显地看出，凸轮实际廓线本身出现了交叉。

在加工凸轮时，廓线中交叉的部分将被刀具切去，即产生过度切割现象，从而使从动件不能完全实现预期的运动规律，即产生运动失真。

  ●凸轮廓线出现交叉原因：

    一方面选用的基圆半径太小（rb=25mm），另一方面又试图在凸轮转过一周中相对小的角度（Φ=90°）时，推动从动件移动过大的升距离（h=100mm）。

   防止出现运动失真的两种办法：

   1）减小从动件的升距h，或增大相应的凸轮转角Φ，但若工作所要求的Φ及h不允许改变，则不能采用这种办法；

   2）不改变工作所要求的Φ及h值，而选用较大的基圆半径，这样做虽然会使凸轮的实际尺寸变大，但当基圆半径增大到一定值时，可以避免运动失真现象。

教学内容提要

时间分配及备注

本次课总结：

本章的重点是凸轮机构的运动设计。

它涉及到：

根据适用场合和工作要求选择凸轮机构的型式、根据工作要求和使用场合选择或设计从动件的运动规律、合理选择凸轮的基圆半径、正确设计出凸轮廓线、对设计出来的凸轮机构进行分析以校核其是否满足设计要求。

第页

教学目的

及要求

1、掌握凸轮廓线设计的基本原理

2、凸轮轮廓曲线的绘制

3、掌握凸轮机构压力角与基圆半径的关系

4、了解用解析法设计凸轮廓线

教学重点

与难点

重点：

凸轮廓线设计的基本原理；凸轮轮廓曲线的绘制；压力角与基圆半径的关系

难点：

反转法的理解；反转法的灵活运用。

教学手段

CAI（动画）、板书（即兴讲解）、结合

参考资料

参看其它有关教材及论文

课后小结

课后根据课堂教学效果总结

作业

习题