八年级数学知识点总结.docx

八年级数学知识点总结.docx

《八年级数学知识点总结.docx》由会员分享，可在线阅读，更多相关《八年级数学知识点总结.docx（11页珍藏版）》请在冰豆网上搜索。

八年级数学知识点总结

八年级数学（上）知识点

人教版八年级上册主要包括三角形、全等三角形、轴对称、整式的乘除与分解因式和分式五个章节的内容。

第十一章三角形

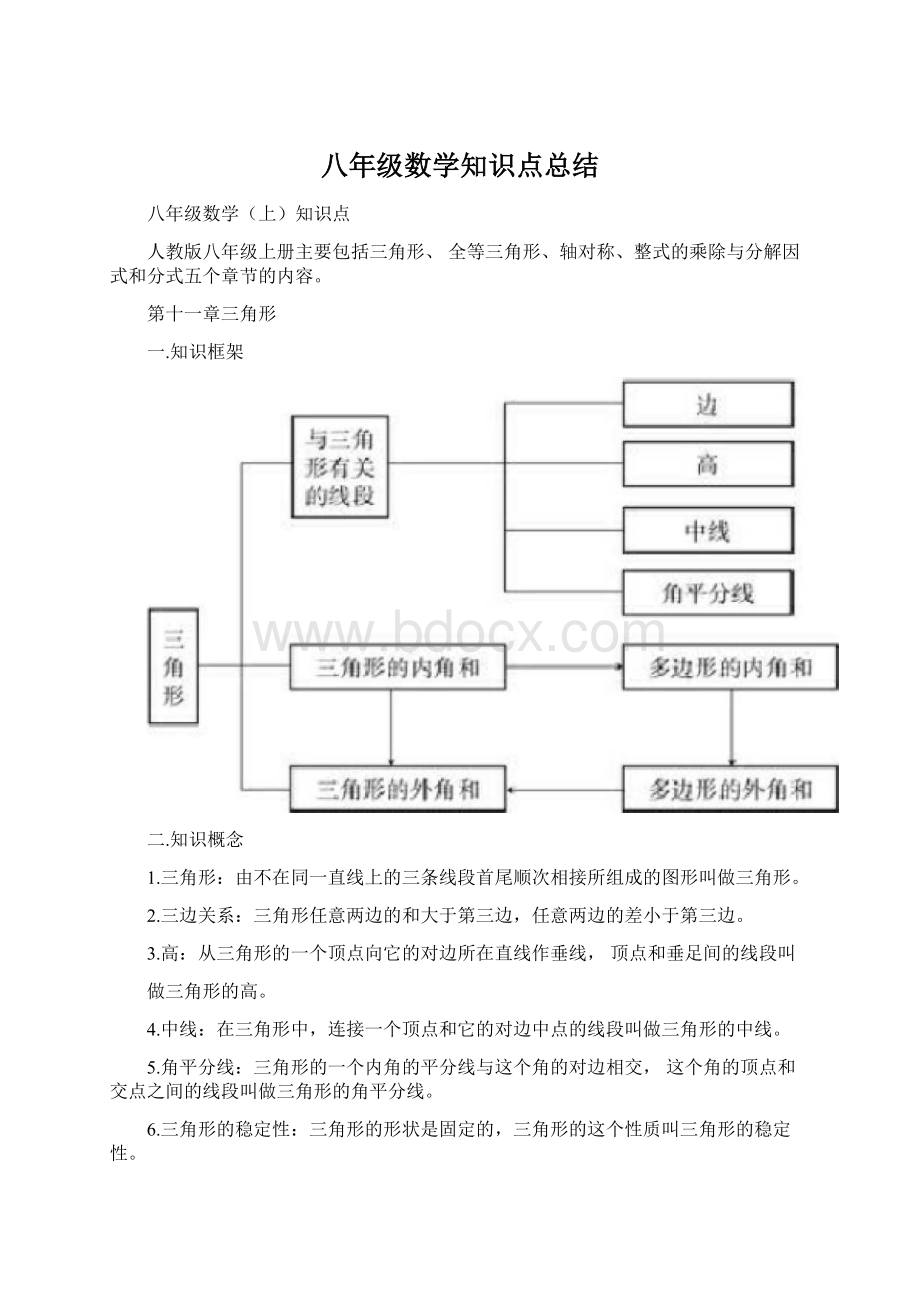
一.知识框架

二.知识概念

1.三角形：

由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。

2.三边关系：

三角形任意两边的和大于第三边，任意两边的差小于第三边。

3.高：

从三角形的一个顶点向它的对边所在直线作垂线，顶点和垂足间的线段叫

做三角形的高。

4.中线：

在三角形中，连接一个顶点和它的对边中点的线段叫做三角形的中线。

5.角平分线：

三角形的一个内角的平分线与这个角的对边相交，这个角的顶点和交点之间的线段叫做三角形的角平分线。

6.三角形的稳定性：

三角形的形状是固定的，三角形的这个性质叫三角形的稳定性。

7.多边形：

在平面内，由一些线段首尾顺次相接组成的图形叫做多边形。

8.多边形的内角：

多边形相邻两边组成的角叫做它的内角。

9.多边形的外角：

多边形的一边与它的邻边的延长线组成的角叫做多边形的外角。

10多边形的对角线：

连接多边形不相邻的两个顶点的线段，叫做多边形的对角线。

11.正多边形：

在平面内，各个角都相等，各条边都相等的多边形叫做正多边形。

12.公式与性质

三角形的内角和：

三角形的内角和为180°

三角形外角的性质：

性质1:

三角形的一个外角等于和它不相邻的两个内角的和。

性质2:

三角形的一个外角大于任何一个和它不相邻的内角。

多边形内角和公式：

n边形的内角和等于（n-2）•180°

多边形的外角和：

多边形的内角和为3600o

多边形对角线的条数：

（1）从n边形的一个顶点出发可以引（n-3）条对角线，把多边形分词（n-2）个三角形。

（2）n边形共有"上2条对角线。

2

三角形是初中数学中几何部分的基础图形，在学习过程中，教师应该多鼓励学生动脑动手，发现和探索其中的知识奥秘。

注重培养学生正确的数学情操和几何思维能力。

第十二章全等三角形

一.知识框架

二.知识概念

1.全等三角形：

两个三角形的形状、大小、都一样时，其中一个可以经过平移、旋转、对称等运动（或称变换）使之与另一个重合，这两个三角形称为全等三角

2,全等三角形的性质：

全等三角形的对应角相等、对应边相等。

3.三角形全等的判定公理及推论有：

（1）“边角边”简称“SA6

（2）“角边角”简称“ASA

（3）“边边边”简称“SS6

（4）“角角边”简称“AAS

（5）斜边和直角边相等的两直角三角形（HD。

4.角平分线推论：

角的内部到角的两边的距离相等的点在叫的平分线上。

5.证明两三角形全等或利用它证明线段或角的相等的基本方法步骤：

①、确定已

知条件（包括隐含条件，如公共边、公共角、对顶角、角平分线、中线、高、等腰三角形、等所隐含的边角关系），②、回顾三角形判定，搞清我们还需要什么，③、正确地书写证明格式（顺序和对应关系从已知推导出要证明的问题）.

在学习三角形的全等时，教师应该从实际生活中的图形出发，引出全等图形进而引出全等三角形。

通过直观的理解和比较发现全等三角形的奥妙之处。

在经历三角形的角平分线、中线等探索中激发学生的集合思维，启发他们的灵感，使学生体会到集合的真正魅力。

第十三章轴对称

一.知识框架

二.知识概念

1.对称轴：

如果一个图形沿某条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形；这条直线叫做对称轴。

2.性质：

（1）轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线。

（2）角平分线上的点到角两边距离相等。

（3）线段垂直平分线上的任意一点到线段两个端点的距离相等。

（4）与一条线段两个端点距离相等的点，在这条线段的垂直平分线上。

（5）轴对称图形上对应线段相等、对应角相等。

3.等腰三角形的性质：

等腰三角形的两个底角相等，（等边对等角）

4.等腰三角形的顶角平分线、底边上的高、底边上的中线互相重合，简称为“三

线合一”。

5.等腰三角形的判定：

等角对等边。

6.等边三角形角的特点：

三个内角相等，等于60°,

7.等边三角形的判定：

三个角都相等的三角形是等腰三角形。

有一个角是60°的等腰三角形是等边三角形

有两个角是60°的三角形是等边三角形。

8.直角三角形中，30°角所对的直角边等于斜边的一半。

9.直角三角形斜边上的中线等于斜边的一半。

本章内容要求学生在建立在轴对称概念的基础上，能够对生活中的图形进行分析鉴赏，亲身经历数学美，正确理解等腰三角形、等边三角形等的性质和判定，并利用这些性质来解决一些数学问题。

第十四章整式的乘除与分解因式

mnm“n

1.同底数幕的乘法法则：

aa=a（m,n都是正数）

/m、nmn

2.1.的乘方法则：

（a）=a（m,n都是正数）

般地，（-a）n=

an（当n为偶数时），

-an（当n为奇数时）.

3.整式的乘法

（1）单项式乘法法则：

单项式相乘，把它们的系数、相同字母分别相乘，对于只在一个单项式里含有的字母，连同它的指数作为积的一个因式。

（2）单项式与多项式相乘：

单项式乘以多项式，是通过乘法对加法的分配律，把它转化为单项式乘以单项式，即单项式与多项式相乘，就是用单项式去乘多项式的每一项，再把所得的积相加。

（3）.多项式与多项式相乘

多项式与多项式相乘，先用一个多项式中的每一项乘以另一个多项式的每一项,再把所得的积相加。

2.2

4.平方差公式：

（a+b）（a-b）=a-b

6.同底数幕的除法法则：

同底数幕相除,底数不变,指数相减，即am，an=am"

（aw0,m、n都是正数，且m>n）.

在应用时需要注意以下几点：

①法则使用的前提条件是“同底数幕相除”而且0不能做除数，所以法则中aw0.00

②任何不等于0的数的0次幕等于1,即a=1（2#0）,如10=1,（-2.5°=1），则0°

无意义.

③任何不等于0的数的-p次幕（p是正整数），等于这个数的p的次幕的倒数，即

（aw0,p是正整数）,而0—1,0—3都是无意义的；当a>0时,a-p的值一定是

21上1

（-2）2）—（―2）——正的；当a<0时,ap的值可能是正也可能是负的，如4,8

④运算要注意运算顺序.

7.整式的除法

单项式除法单项式：

单项式相除，把系数、同底数幕分别相除，作为商的因式，对于只在被除式里含有的字母，则连同它的指数作为商的一个因式；

多项式除以单项式：

多项式除以单项式，先把这个多项式的每一项除以单项式，再把所得的商相加.

8.分解因式：

把一个多项式化成几个整式的积的形式，这种变形叫做把这个多项式分解因式一.

分解因工而一般方法：

1.提公共因式法2.运用公式法3.十字相乘法

分解因式的步骤：

（1）先看各项有没有公因式，若有，则先提取公因式；

⑵再看能否使用公式法；

（3）用分组分解法，即通过分组后提取各组公因式或运用公式法来达到分解的目

的；

（4）因式分解的最后结果必须是几个整式的乘积，否则不是因式分解；

（5）因式分解的结果必须进行到每个因式在有理数范围内不能再分解为止.

整式的乘除与分解因式这章内容知识点较多，表面看来零碎的概念和性质也

较多，但实际上是密不可分的整体。

在学习本章内容时，应多准备些小组合作与交流活动，培养学生推理能力、计算能力。

在做题中体验数学法则、公式的简洁美、和谐美，提高做题效率。

八年级数学（下）知识点

人教版八年级下册主要包括了二次根式、勾股定理、平行四边形、一次函数、数据的分析五章内容。

第十六章二次根式

一.知识框架

二.知识概念

二次根式：

一般地，形如，a（a>0）的代数式叫做二次根式。

当a>0时，Va

表示a的算数平方根,其中，0二0

对于本章内容，教学中应达到以下几方面要求：

1.理解二次根式的概念，了解被开方数必须是非负数的理由；

2.了解最简二次根式的概念；

3.理解并掌握下列结论：

1）是非负数；

（2）［痛Y=口9之°）;（3）必39*0;

4.掌握二次根式的加、减、乘、除运算法则，会用它们进行有关实数的简单四

则运算；

5.了解代数式的概念，进一步体会代数式在表示数量关系方面的作用。

第十八章勾股定理

一.知识框架

1.勾股定理：

如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2。

勾股定理逆定理：

如果三角形三边长a,b,c满足a2+b2=c2。

，那么这个三角形是直角三角形。

2.定理：

经过证明被确认正确的命题叫做定理。

3.我们把题设、结论正好相反的两个命题叫做互逆命题。

如果把其中一个叫做原

命题，那么另一个叫做它的逆命题。

（例：

勾股定理与勾股定理逆定理）

勾股定理是直角三角形具备的重要性质。

本章要求学生在理解勾股定理的前提下，学会利用这个定理解决实际问题。

可以通过自主学习的发展体验获取数学知识的感受。

二.知识概念

1.平行四边形定义：

有两组对边分别平行的四边形叫做平行四边形。

2.平行四边形的性质：

平行四边形的对边相等；平行四边形的对角相等。

平行四边形的对角线互相平分。

3

.平行四边形的判定

（1）.两组对边分别相等的四边形是平行四边形

2）.对角线互相平分的四边形是平行四边形；

3）

4）一组对边平行且相等的四边形是平行四边形。

.两组对角分别相等的四边形是平行四边形;

4

.三角形的中位线平行于三角形的第三边，且等于第三边的一半。

5.直角三角形斜边上的中线等于斜边的一半。

6.矩形的定义：

有一个角是直角的平行四边形。

7.矩形的性质：

矩形的四个角都是直角；矩形的对角线平分且相等。

8.矩形判定定理：

（1）.有一个角是直角的平行四边形叫做矩形

2.对角线相等的平行四边形是矩形。

3）.有三个角是直角的四边形是矩形。

9.菱形的定义：

邻边相等的平行四边形。

10.菱形的性质：

菱形的四条边都相等；菱形的两条对角线互相垂直,并且每一条对角线平分一组对角o

11.菱形的判定定理：

（1）.一组邻边相等的平行四边形是菱形

②）对角线互相垂直的平行四边形是菱形

3）四条边相等的四边形是菱形。

12

.S菱形=1/2Xab（a、b为两条对角线）

13.正方形定义：

一个角是直角的菱形或邻边相等的矩形。

14.正方形的性质：

四条边都相等，四个角都是直角。

正方形既是矩形，又是菱

形。

15.正方形判定定理：

1.邻边相等的矩形是正方形。

2

.有一个角是直角的菱形是正方形。

16.梯形的定义：

一组对边平行，另一组对边不平行的四边形叫做梯形。

17.直角梯形的定义：

有一个角是直角的梯形

18.等腰梯形的定义：

两腰相等的梯形。

19.等腰梯形的性质：

等腰梯形同一底边上的两个角相等；等腰梯形的两条对角线相等。

20.等腰梯形判定定理：

同一底上两个角相等的梯形是等腰梯形。

本章内容是对平面上四边形的分类及性质上的研究，要求学生在学习过程中多动手多动脑，把自己的发现和知识带入做题中。

因此教师在教学时可以多鼓励学生自己总结四边形的特点，这样有利于学生对知识的把握。

第十九章一次函数

一.知识框架

1

.一次函数：

若两个变量x,y间的关系式可以表示成y=kx+b（k*0）的形式，则称y是x的一次函数（x为自变量,y为因变量）。

特别地,当b=0时，称y是x的正比

b.0

kc01b=0

、b<0

2.正比例函数一般式：

y=kx（kw0）,其图象是经过原点（0,0）

3.正比例函数y=kx（kw0）的图象是一条经过原点的直线，当k>0时，直线y=kx

经过第一、三象限,y随x的增大而增大，当k<0时，直线y=kx经过第二、四象限,y随x的增大而减小，在一次函数y=kx+b中：

当k>0时,y随x的增大而增大；当k<0时,y随x的增大而减小。

4.已知两点坐标求函数解析式：

待定系数法

一次函数是初中学生学习函数的开始，也是今后学习其它函数知识的基石。

在学习本章内容时，教师应该多从实际问题出发，引出变量，从具体到抽象的认识事物。

培养学生良好的变化与对应意识，体会数形结合的思想。

在教学过程中，应更加侧重于理解和运用，在解决实际问题的同时，让学习体会到数学的实用价值和乐趣。

第二十章数据的分析

一.知识框架

二.知识概念

1.加权平均数：

加权平均数的计算公式。

权的理解：

反映了某个数据在整个数

据中的重要程度。

2.中位数：

将一组数据按照由小到大（或由大到小）的顺序排列，如果数据的个

数是奇数，则处于中间位置的数就是这组数据的中位数（median）；如果数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数。

3.众数：

一组数据中出现次数最多的数据就是这组数据的众数（mode。

4.极差：

组数据中的最大数据与最小数据的差叫做这组数据的极差（range）

5.方差越大，数据的波动越大；方差越小，数据的波动越小，就越稳定。

本章内容要求学生在经历数据的收集、整理、分析过程中发展学生的统计

意识和数据处理的方法与能力。

在教学过程中，以生活实例为主，让学生体会到数据在生活中的重要性。