专题二次函数与几何图形综合图形面积问题后附答案精品.docx

专题二次函数与几何图形综合图形面积问题后附答案精品.docx

《专题二次函数与几何图形综合图形面积问题后附答案精品.docx》由会员分享，可在线阅读，更多相关《专题二次函数与几何图形综合图形面积问题后附答案精品.docx（13页珍藏版）》请在冰豆网上搜索。

专题二次函数与几何图形综合图形面积问题后附答案精品

专题二次函数与几何图形综合——图形面积问题

类型1　已知三角形的面积，求点的坐标

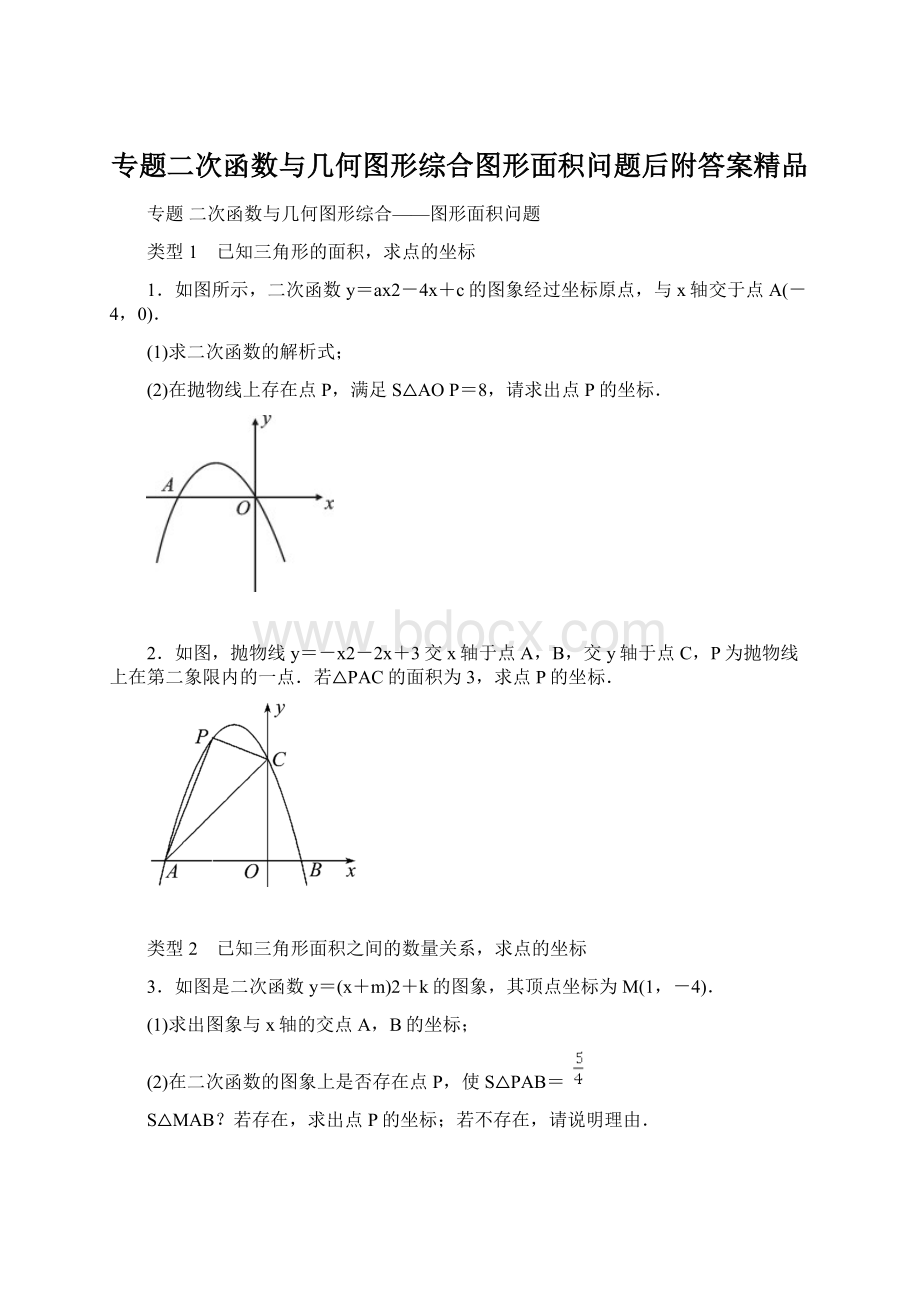
1．如图所示，二次函数y＝ax2－4x＋c的图象经过坐标原点，与x轴交于点A（－4，0）．

（1）求二次函数的解析式；

（2）在抛物线上存在点P，满足S△AOP＝8，请求出点P的坐标．

2．如图，抛物线y＝－x2－2x＋3交x轴于点A，B，交y轴于点C，P为抛物线上在第二象限内的一点．若△PAC的面积为3，求点P的坐标．

类型2　已知三角形面积之间的数量关系，求点的坐标

3．如图是二次函数y＝（x＋m）2＋k的图象，其顶点坐标为M（1，－4）．

（1）求出图象与x轴的交点A，B的坐标；

（2）在二次函数的图象上是否存在点P，使S△PAB＝

S△MAB？

若存在，求出点P的坐标；若不存在，请说明理由．

类型3　求三角形面积的最值

4．如图，直线l：

y＝－3x＋3与x轴、y轴分别相交于A，B两点，抛物线y＝ax2－2ax＋a＋4（a＜0）经过点B.

（1）求该抛物线的函数解析式；

（2）已知点M是抛物线上的一个动点，并且点M在第一象限内，连接AM，BM.设点M的横坐标为m，△ABM的面积为S，求S关于m的函数解析式，并求出S的最大值．

类型4　求四边形的面积

5．如图，二次函数的图象与x轴交于A（－2，0），B（4，0）两点，且函数的最大值为9.

（1）求二次函数的解析式；

（2）设此二次函数图象的顶点为C，与y轴交点为D，求四边形ABCD的面积．

类型5　求四边形面积的最值

6．如图，抛物线y=ax2+bx+c（a、b、c为常数，a≠0）经过点A（﹣1，0），B（5，﹣6），C（6，0）．

（1）求抛物线的解析式；

（2）如图，在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大？

若存在，请求出点P的坐标；若不存在，请说明理由；

（3）若点Q为抛物线的对称轴上的一个动点，试指出△QAB为等腰三角形的点Q一共有几个？

并请求出其中某一个点Q的坐标．

7.如图，抛物线y=ax2+bx+c经过A （-1，0）、B （3，0）、C （0，3）三点，对称轴与抛物线相交于点P、与直线BC相交于点M．

（1）求该抛物线的解析式：

______；

（2）在BC上方的抛物线上是否存在一点K，使四边形ABKC的面积最大？

若存在，求出K点的坐标及最大面积；

（3）连接CP，在第一象限的抛物线上是否存在一点R，使△RPM与△RMB的面积相等？

若存在，求出点R的坐标；若不存在，说明理由．

参考答案：

1.解：

（1）由已知条件，得

解得

∴此二次函数的解析式为y＝－x2－4x.

（2）∵点A的坐标为（－4，0），∴AO＝4.

设点P到x轴的距离为h，则S△AOP＝

×4h＝8.

解得h＝4.

①当点P在x轴上方时，－x2－4x＝4.

解得x＝－2.

∴点P的坐标为（－2，4）．

②当点P在x轴下方时，－x2－4x＝－4.

解得x1＝－2＋2

，x2＝－2－2

.

∴点P的坐标为（－2＋2

，－4）或（－2－2

，－4）．

综上所述，点P的坐标是（－2，4），（－2＋2

，－4），（－2－2

，－4）．

2.解：

如图，过点P作PQ平行于y轴，交AC于点Q.

由题意，得A（－3，0），C（0，3），

∴直线AC的解析式为y＝x＋3.

设点P（x，－x2－2x＋3），则点Q（x，x＋3），

∴PQ＝－x2－2x＋3－（x＋3）＝－x2－3x，∴S△PAC＝

PQ·OA，∴

（－x2－3x）×3＝3，解得x1＝－1，x2＝－2.当x＝－1时，点P的坐标为（－1，4）；

当x＝－2时，点P的坐标为（－2，3）．

综上所述，点P的坐标为（－1，4）或（－2，3）．

3.解：

（1）∵抛物线y＝（x＋m）2＋k的顶点坐标为M（1，－4），

∴y＝（x－1）2－4.

令y＝0，即（x－1）2－4＝0.

解得x1＝3，x2＝－1.

∴A（－1，0），B（3，0）．

（2）∵△PAB与△MAB同底，且S△PAB＝

S△MAB，

∴|yP|＝

|yM|＝

×4＝5，即yP＝±5.

又∵点P在二次函数y＝（x－1）2－4的图象上，

∴yP≥－4.∴yP＝5.

∴（x－1）2－4＝5，解得x1＝4，x2＝－2.

∴存在这样的点P，其坐标为（4，5）或（－2，5）．

4.解：

（1）直线l：

y＝－3x＋3与x轴、y轴分别相交于A，B两点，则点A，B的坐标分别为（1，0），（0，3）．抛物线y＝ax2－2ax＋a＋4（a＜0）经过点B（0，3），则a＋4＝3，解得a＝－1，故抛物线的函数解析式为y＝－x2＋2x＋3.

（2）如图，过点M作MH⊥x轴于点H.

设点M（m，－m2＋2m＋3），则S＝S梯形BOHM－S△OAB－S△AMH＝

（－m2＋2m＋3＋3）×m－

[3×1＋（m－1）（－m2＋2m＋3）]＝－

m2＋

m.∵－

<0，

∴S有最大值，当m＝

时，S的最大值为

.

5.解：

（1）由抛物线的对称性知，它的对称轴是直线x＝

＝1.

又∵函数的最大值为9，

∴抛物线的顶点坐标为（1，9）．

设抛物线的解析式为y＝a（x－1）2＋9，将B（4，0）代入，得a＝－1.

∴二次函数的解析式是y＝－（x－1）2＋9，

即y＝－x2＋2x＋8.

（2）当x＝0时，y＝8，即抛物线与y轴的交点D的坐标为（0，8）．

过点C作CE⊥x轴于点E.

∴S四边形ABCD＝S△AOD＋S四边形DOEC＋S△BCE

＝

×2×8＋

×（8＋9）×1＋

×3×9

＝30.

6.解：

（1）设y=a（x+1）（x﹣6）（a≠0），

把B（5，﹣6）代入：

a（5+1）（5﹣6）=﹣6，

a=1，

∴y=（x+1）（x﹣6）=x2﹣5x﹣6；

（2）存在，

如图1，分别过P、B向x轴作垂线PM和BN，垂足分别为M、N，

设P（m，m2﹣5m﹣6），四边形PACB的面积为S，

则PM=﹣m2+5m+6，AM=m+1，MN=5﹣m，CN=6﹣5=1，BN=5，

∴S=S△AMP+S梯形PMNB+S△BNC

=

（﹣m2+5m+6）（m+1）+

（6﹣m2+5m+6）（5﹣m）+

×1×6

=﹣3m2+12m+36

=﹣3（m﹣2）2+48，

当m=2时，S有最大值为48，这时m2﹣5m﹣6=22﹣5×2﹣6=﹣12，

∴P（2，﹣12），

（3）这样的Q点一共有5个，连接Q3A、Q3B，

y=x2﹣5x﹣6=（x﹣

）2﹣

；

因为Q3在对称轴上，所以设Q3（

，y），

∵△Q3AB是等腰三角形，且Q3A=Q3B，

由勾股定理得：

（

+1）2+y2=（

﹣5）2+（y+6）2，

y=﹣

，

∴Q3（

，﹣

）．

7.解：

（1）把三点代入抛物线解析式

解得：

所以二次函数式为y=-x2+2x+3；

（2）设存在点K，使得四边形ABKC的面积最大

∵点K在抛物线y=-x2+2x+3上，

∴设点K的坐标为：

（x，-x2+2x+3），

作KN⊥AB于点N，

根据题意得：

AO=1，OC=3，ON=x，BN=3-x，KN=-x2+2x+3，

∴S四边形ABKC=S△AOC+S梯形ONKC+S△BNK

=

AO•CO+

（OC+KN）•ON+

KN•BN

=

×1×3+

×（3-x2+2x+3）•x+

×（x-3）（-x2+2x+3）

=-

x2+

x+6

=-

（x-

）2+

，

∵x=

时，-x2+2x+3=

，

∴在BC上方的抛物线上存在一点K（

，

），使四边形ABKC的面积最大，最大面积为

；

（3）由题意求得直线BC代入x=1，则y=2，

∴M（1，2），

由点M，P的坐标可知：

点R存在，即过点M平行于x轴的直线，

则代入y=2，x2-2x-1=0，

解得x=1-

（在对称轴的左侧，舍去），x=1+

，即点R（1+

，2）．