数字信号处理实验15含代码.docx

数字信号处理实验15含代码.docx

《数字信号处理实验15含代码.docx》由会员分享，可在线阅读，更多相关《数字信号处理实验15含代码.docx（21页珍藏版）》请在冰豆网上搜索。

数字信号处理实验15含代码

实验一离散时间信号的时域分析

1.在MATLAB中利用逻辑关系式

来实现

序列，显示围

。

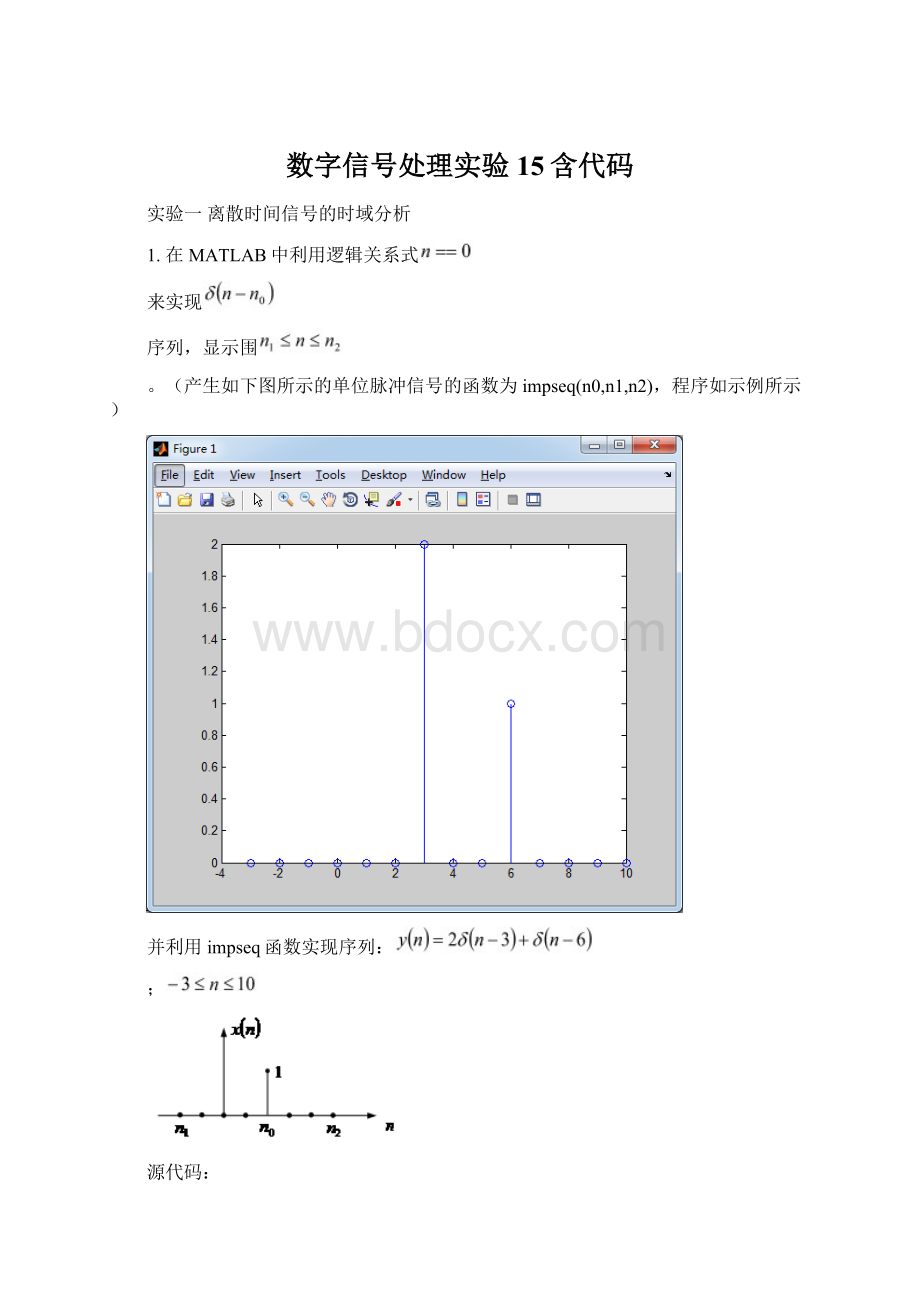
（产生如下图所示的单位脉冲信号的函数为impseq（n0,n1,n2），程序如示例所示）

并利用impseq函数实现序列：

；

源代码：

impseq.m

functiony=impseq（n0,n1,n2）

n=[n1:

n2]

y=[（n-n0）==0]

exp01-1.m

functionimpseq（n0,n1,n2）

n=-3:

1:

10

y=2*impseq（3,-3,10）+impseq（6,-3,10）;

stem（n,y）

2.在MATLAB中利用逻辑关系式

来实现

序列，显示围

。

（自己编写产生单位阶跃信号的函数，函数命名为stepseq（n0,n1,n2））

并利用编写的stepseq函数实现序列：

源代码：

stepseq.m

functiony=stepseq（n0,n1,n2）

n=n1:

1:

n2

y=[（n-n0）>=0]

exp01-2.m

functionstepseq（n0,n1,n2）

n=-5:

1:

20

y=stepseq（-2,-5,20）+stepseq（2,-5,20）

stem（n,y）

3.在MATLAB中利用数组运算符“.^”来实现一个实指数序列。

如：

源代码：

n=0:

1:

15;

x=0.3.^n

stem（n,x）

4.在MATLAB中调用函数sin或cos产生正余弦序列，如：

源代码：

n=0:

1:

20

x=11*sin（0.3*pi*n+pi/5）+5*cos（0.3*pi*n）

stem（n,x）

思考题：

1.在MATLAB环境下产生单位脉冲序列和单位阶跃序列各有几种方法？

如何使用？

2.在MATLAB环境下进行序列的相乘运算时应注意什么问题？

实验二离散时间系统的时域分析

1.在MATLAB中利用部函数conv来计算两个有限长序列的卷积。

给出两个序列，试求其卷积结果。

源代码：

x=[5,9,3,6,-8];

h=[18,7,5,20,11,14,9];

n=[-4:

6]

y=conv（x,h）

stem（n,y）

运行结果：

n=

-4-3-2-10123456

y=

901971422741482032842923-58-72

2.在MATLAB中利用filter函数在给定输入和差分方程时求差分方程的解。

给出如下差分方程：

（1）计算并画出冲击响应

（2）由此

确定系统是否稳定。

（稳定）

源代码：

b=[1];

a=[1,-0.9,0.5];

n=-10:

50;

x=[zeros（1,10）,1,zeros（1,10）];

y=filter（b,a,x）;

n=[-10:

10]

stem（n,y）

3.已知系统单位脉冲响应为

，如果输入为

，求利用conv函数求系统输出

。

源代码：

n=[0:

19]

h=cos（0.5*n）+sin（0.2*n）

m=[0:

9]

x=exp（0.2*m）

y=conv（x,h）

stem（y）

思考题：

1.离散线性时不变系统中的差分方程和系统函数有何联系？

公式中的系数在编写程序时须注意什么问题？

系统函数H（Z）=Y（Z）/X（Z）,对差分方程进行Z变换，由公式得系统函数。

 由差分方程进行z变换可以求得系统函数。

公式中的系数应从低阶向高阶写，没有的项补零。

公式中的系数在编写程序时须注意：

y（n）的系数必须为1，注意不要落下潜在的0系数。

2.MATLAB中提供的conv卷积子函数使用中须满足什么条件？

如果条件不满足应如何处理？

conv中卷积的子函数n值是从零开始的，如果不满足此条件，需从新定义卷积结果的n值围。

实验三离散时间系统的频域分析

1.已知离散时间系统函数为

求该系统的零极点（提示：

可以用roots实现）；画出零极点分布图（提示：

可以用zplane实现）；判断系统的因果、稳定性。

源代码：

b=[0.20.10.30.10.2];

a=[1-1.11.5-0.70.3];

z=roots（b）;

p=roots（a）;

zplane（b,a）

disp（z）

disp（p）

disp（abs（z））

disp（abs（p））

2.已知离散时间系统的系统函数为

求该系统在

频率围的幅频响应、相频响应。

（提示：

用freqz、abs和angle实现）

源代码：

b=[0.20.10.30.10.2];

a=[1-1.11.5-0.70.3];

[h,w]=freqz（b,a）;

hf=abs（h）;

hx=angle（h）;

subplot（211），plot（w,hf）

title（'幅频响应'）

xlabel（'x'）

ylabel（'|X（e^jx）|'）

subplot（212）

plot（w,hx）

title（'相频响应'）

xlabel（'x'）

3.已知序列

，

，

，

，求

、g（n）、y（n）、h（n）的DFT。

要求：

（1）画出各DFT的幅频特性和相频特性图（包括

、

、

、

图形）；（提示：

可考虑用FFT计算DFT；幅频特性用abs函数；相频特性用angle函数）；

（2）比较四种信号的频谱，看能得出什么结论？

源代码：

x=[8,4,2,1],n=0:

1:

3

X=fft（x）,V=abs（X）,W=angle（X）

subplot（241）,stem（n,V）,title（'|X（k）|'）

subplot（242）,stem（n,W）,title（'arg|X（k）]'）

g=[8,4,2,1,0,0,0,0],n=0:

1:

7

G=fft（g）,V=abs（G）,W=angle（G）

subplot（243）,stem（n,V）,title（'|G（k）|'）

subplot（244）,stem（n,W）,title（'arg|G（k）]'）

y=[8,0,4,0,2,0,1,0],n=0:

1:

7

Y=fft（y）,V=abs（Y）,W=angle（Y）

subplot（245）,stem（n,V）,title（'|Y（k）|'）

subplot（246）,stem（n,W）,title（'arg|Y（k）]'）

h=[8,4,2,1,8,4,2,1],n=0:

1:

7

H=fft（h）,V=abs（H）,W=angle（H）

subplot（247）,stem（n,V）,title（'|H（k）|'）

subplot（248）,stem（n,W）,title（'arg|H（k）]'）

思考题：

1.使用MATLAB语言提供的快速傅里叶变换有关子函数进行有限长和无限长序列频谱分析时需注意哪些问题？

在使用fft函数时，对于有限长和无限长序列要注意点数N的问题。

对于有限长序列，其N值一般为该序列的长度；而对于无限长序列频谱分析时，首先要将无限长序列截断成有一个有限长序列，此时序列长度的取值N对频谱有较大的影响。

一般来讲，N值取得越大，曲线精度越高。

2.因果稳定的离散系统必须满足的充分必要条件是什么？

系统函数零极点的位置与系统冲激响应有何关系？

对系统的幅度响应有何影响？

因果稳定的离散系统必须满足的充分必要条件是其系统函数的收敛域必须包含单位圆的圆外区域。

系统函数零极点的位置与系统冲激响应的关系：

零点的位置影响冲激响应的幅度大小，而极点位置影响冲激响应包络的变化趋势，当其极点在单位圆，则冲击响应的包络会随n值的增大而衰减；如果极点在单位圆上，则包络不随n而变化；若极点在单位圆外。

则冲激响应的包络将随n值的增大而增大。

系统函数的零极点位置与系统幅频响应的关系是：

在极点所在频率位置附近，幅度出现峰值，极点越靠近单位圆峰值越尖锐；在零点所在频率位置附近，频率响应幅度出现谷点，当零点在单位圆上时谷点为零值。

实验四IIR数字滤波器的设计

1.利用脉冲响应不变法，用巴特沃斯滤波器原型设计一个低通滤波器，满足：

，采样频率为10000Hz。

（提示信息：

利用函数buttord，butter，impinvar）

源代码：

fs=10000;

T=1/fs;

Wp=0.2*pi/T;

Ws=0.3*pi/T;

Ap=1;

As=15;

[N,Wc]=buttord（Wp,Ws,Ap,As,'s'）;

[B,A]=butter（N,Wc,'s'）;

W=linspace（0,pi,400*pi）;

[D,C]=impinvar（B,A,fs）;

Hz=freqz（D,C,W）;

plot（W/pi,abs（Hz）/abs（Hz

（1）））;

gridon;title（'巴特沃斯数字滤波器'）;

xlabel（'Frequency/Hz'）;ylabel（'Magnitude'）

2.设计巴特沃斯低通数字滤波器，满足：

采样频率Fs=10000Hz，

。

（提示信息：

利用函数buttord，butter）

源代码：

fs=10000;%采样频率

T=1/fs;

Wp=0.2*pi/pi;

Ws=0.3*pi/pi;%根据ω=ΩT设置通带和阻带模拟域截止频率

Rs=15;%设置通带最大和最小衰减

Rp=1;[N,Wc]=buttord（Wp,Ws,Rp,Rs）;%确定巴特沃斯模拟滤波器阶数和截止频率

W=linspace（0,pi,400*pi）;%指定一段频率值

Nn=length（W）;[B,A]=butter（N,Wc）;%确定巴特沃斯模拟滤波器传递函数H（s）

Hz=freqz（B,A,Nn,fs）;%返回频率响应

plot（W/pi,abs（Hz）/abs（Hz

（1）））;%绘出巴特沃斯数字低通滤波器的幅频特性曲线或plot（abs（Hz））;

gridon;

ylabel（'Magnitude'）;

xlabel（'Frequency/Hz'）;

title（'巴特沃斯数字滤波器'）;

3.设计巴特沃斯高通数字滤波器，满足：

通带截止频率wp=400Hz，阻带截止频率ws=200Hz，通带最大衰减rp=3dB，阻带最小衰减rs=15dB，采样频率为1000Hz。

（提示信息：

利用函

数buttord，butter）

源代码：

fp=400

fs=200;

rp=3;

rs=15;

wp=fp*2*pi;

ws=fs*2*pi;

FS=1000;

T=1/FS;

Wp=wp/（FS）;

Ws=ws/（FS）;

wp2=2*tan（Wp/2）/T;

ws2=2*tan（Ws/2）/T;

[n,Wc]=buttord（wp2,ws2,rp,rs,'s'）;

[b,a]=butter（n,Wc,'high','s'）;

[bz,az]=bilinear（b,a,FS）;

[H,W]=freqz（bz,az,256）;

plot（W*FS/（2*pi）,abs（H））;

gridon;

xlabel（'频率/Hz'）;

ylabel（'幅值'）;

4.设计切比雪夫I型和切比雪夫II型IIR带通数字滤波器，满足：

wp1=60Hz，wp2=80Hz，ws1=55Hz，ws2=85Hz，通带最大衰减rp=0.5dB，阻带最小衰减rs=60dB，采样频率Fs=200Hz。

（提示信息：

利用函数cheb1ord，cheby1和cheb2ord，cheby2）

源代码：

wp1=60;

wp2=80;

ws1=55;

ws2=85;

rp=0.5;

rs=60;

Fs=200;

[N,Wn]=cheb1ord（[wp1,wp2]/（Fs/2）,[ws1,ws2]/（Fs/2）,rp,rs）;%ChebyshevI型滤波器参数计算（数字域）；

[P,Q]=cheby1（N,rp,Wn,'bandpass'）;%创建Chebyshev带通滤波器；

figure

（1）;

freqz（P,Q）;%显示产生滤波器的幅频及相频曲线；

[H,W]=freqz（P,Q）;

figure

（2）;

plot（W*Fs/（2*pi）,abs（H））;

gridon;

xlabel（'频率/Hz'）;

ylabel（'幅度'）;

[N,Wn]=cheb2ord（[wp1,wp2]/（Fs/2）,[ws1,ws2]/（Fs/2）,rp,rs）;%ChebyshevI型滤波器参数计算（数字域）；

[P,Q]=cheby2（N,rp,Wn,'bandpass'）;%创建Chebyshev带通滤波器；

figure（3）;

freqz（P,Q）;%显示产生滤波器的幅频及相频曲线；

[H,W]=freqz（P,Q）;

figure（4）;

plot（W*Fs/（2*pi）,abs（H））;

gridon;

xlabel（'频率/Hz'）;

ylabel（'幅度'）;

5.设计一个椭圆型带阻数字滤波器，满足：

wp1=650Hz，wp2=850Hz，ws1=700Hz，ws2=800Hz，通带最大衰减rp=0.1dB，阻带最小衰减rs=50dB，采样频率Fs=2000Hz。

（提示信息：

利用函数ellipord和ellip）

源代码：

wp1=650;

wp2=850;

ws1=700;

ws2=800;

rp=0.1;

rs=50;

Fs=2000;

wp=[wp1,wp2]/（Fs/2）;

ws=[ws1,ws2]/（Fs/2）;

[N,wc]=ellipord（wp,ws,rp,rs,'z'）;

[num,den]=ellip（N,rp,rs,wc,'stop'）;

[H,W]=freqz（num,den）;

plot（W*Fs/（2*pi）,abs（H））;

gridon

xlabel（'频率/Hz'）;

ylabel（'幅值'）;

实验五FIR数字滤波器的设计

1.用窗函数法设计一个线性相位低通滤波器，满足：

通带截止频率

，阻带截止频率

，阻带衰减不小于50dB，通带波纹不大于1dB。

（提示信息：

方法1：

直接利用函数fir1；方法2：

根据窗函数法设计原理利用窗函数hanning或boxcar或hamming或blackman）

源代码：

wp=0.6*pi;

ws=0.7*pi;

wdelta=ws-wp;

N=ceil（8*pi/wdelta）

ifrem（N,2）==0

N=N+1;

end

Nw=N;

we=（wp+ws）/2;

n=0:

N-1;

alpha=（N-1）/2;

m=n-alpha+0.00001;

hd=sin（we*m）./（pi*m）;

win=（hanning（Nw））';

h=hd.*win;

b=h;

freqz（b,1,512）

N=80;

title（'hanning窗口法'）

2.用频率采样法设计一个高通数字滤波器，满足：

通带截止频率

，阻带截止频率

，在通带和阻带之间增加两个过渡采样点

。

（提示信息：

方法1：

直接利用函数fir2；方法2：

根据频率采样法设计原理利用函数ifft求h（n））

源代码：

M=32;

Wp=0.8*pi;

m=0:

M/2;

Wm=2*pi*m./（M+1）;

mtr=ceil（Wp*（M+1）/（2*pi））;

Ad=[Wm>=Wp];

Ad（mtr）=0.28;

Hd=Ad.*exp（-j*0.5*M*Wm）;

Hd=[Hdconj（fliplr（Hd（2:

M/2+1）））];

h=real（ifft（Hd））;

w=linspace（0,pi,1000）;

H=freqz（h,[1],w）;

figure

（1）

plot（w/pi,20*log10（abs（H）））;

xlabel（'w/pi'）;

ylabel（'幅度（dB）'）;

axis（[01-500]）;

title（'高通数字滤波器'）;