《现代控制理论》课后习题答案5.pdf

《现代控制理论》课后习题答案5.pdf

《《现代控制理论》课后习题答案5.pdf》由会员分享，可在线阅读，更多相关《《现代控制理论》课后习题答案5.pdf（12页珍藏版）》请在冰豆网上搜索。

现代控制理论第现代控制理论第5章习题解答章习题解答5.1已知系统的状态空间模型为已知系统的状态空间模型为CxyBuAxx=+=,?

，画出加入状态反馈后的系统结构图，写出其状态空间表达式。

，画出加入状态反馈后的系统结构图，写出其状态空间表达式。

答：

答：

具有状态反馈的闭环系统状态空间模型为：

uKx=+v（）xABKxBvyCx=+=?

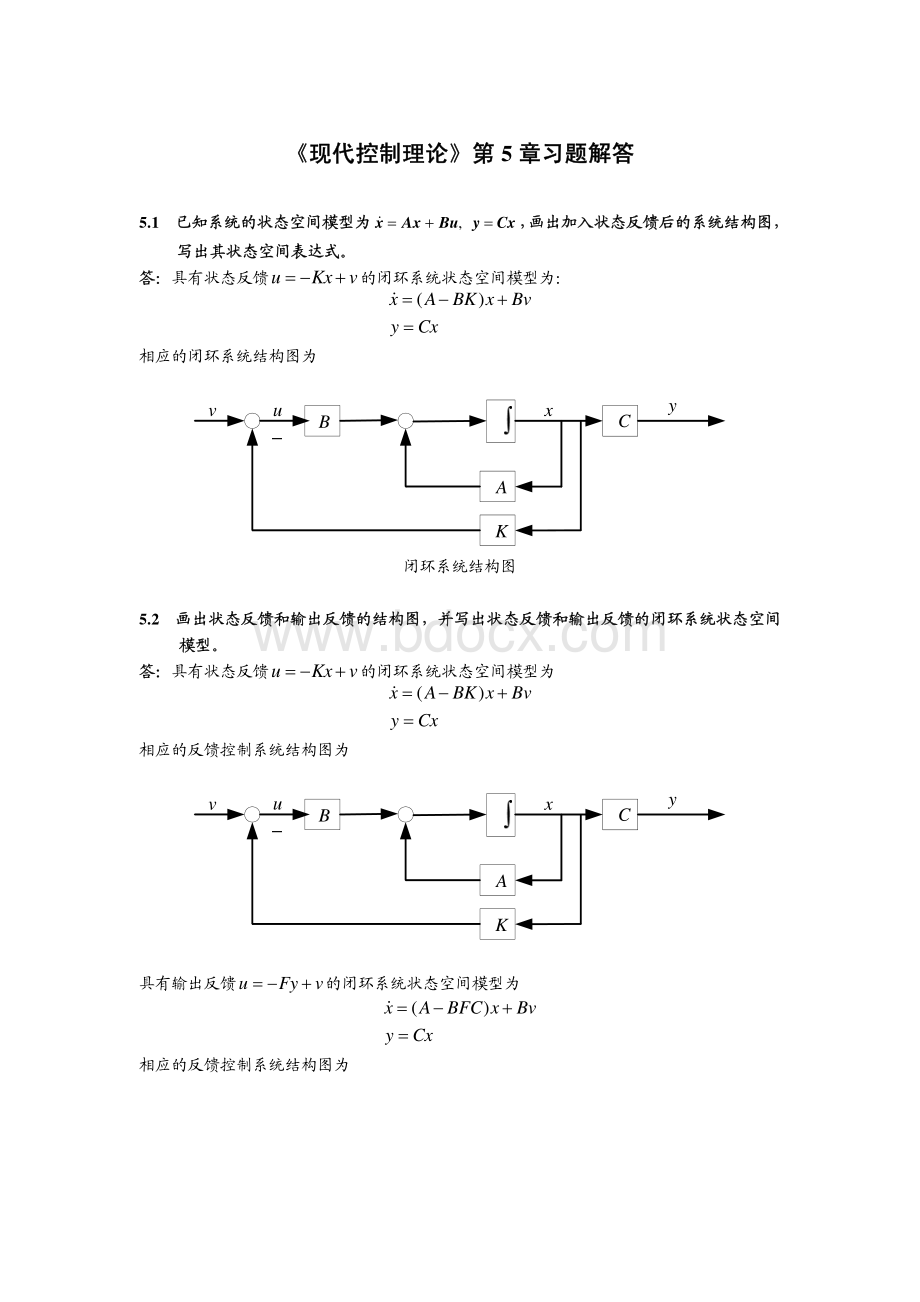
相应的闭环系统结构图为CxAKyBuv闭环系统结构图5.2画出状态反馈和输出反馈的结构图，并写出状态反馈和输出反馈的闭环系统状态空间模型。

画出状态反馈和输出反馈的结构图，并写出状态反馈和输出反馈的闭环系统状态空间模型。

答：

答：

具有状态反馈的闭环系统状态空间模型为uKx=+v（）xABKxBvyCx=+=?

相应的反馈控制系统结构图为CxAKyBuv具有输出反馈的闭环系统状态空间模型为uFy=+v（）xABFCxBvyCx=+=?

相应的反馈控制系统结构图为CxAFyBuv5.3状态反馈对系统的能控性和能观性有什么影响？

输出反馈对系统能控性和能观性的影响如何？

状态反馈对系统的能控性和能观性有什么影响？

输出反馈对系统能控性和能观性的影响如何？

答：

答：

状态反馈不改变系统的能控性，但不一定能保持系统的能观性。

输出反馈不改变系统的能控性和能观性。

5.4通过检验能控性矩阵是否满秩的方法证明定理通过检验能控性矩阵是否满秩的方法证明定理5.1.1。

答：

答：

加入状态反馈后得到闭环系统KS，其状态空间模型为（）xABKxBvyCx=+=?

开环系统的能控性矩阵为0S1,ncABBABAB=?

闭环系统KS的能控性矩阵为1（）,（）（）ncKABKBBABKBABKB=?

由于222（）（）（）（）（ABKBABBKBABKBAABKBKABKBKB）ABABKBBKABKBKB=+=?

以此类推，总可以写成的线性组合。

因此，存在一个适当非奇异的矩阵U，使得（）mABKB1,mmABABABB（）,cKcABKBABU=由此可得：

若rank（,）cABn=，即有个线性无关的列向量，则n（）,cKABKB也有个线性无关的列向量，故nrank（）,）cKABKBn=5.5状态反馈和输出反馈各有什么优缺点。

状态反馈和输出反馈各有什么优缺点。

答：

答：

状态反馈的优点是，不改变系统的能控性，可以获得更好的系统性能。

其缺点是，不能保证系统的能观性，状态x必须可测，成本高。

输出反馈的优点是：

保持系统的能控性和能观性不变，结构简单，只用到外部可测信号。

其缺点是，由于用到的信号少，它所达到的系统性能往往有限，有时甚至都不能达到闭环系统的稳定性。

5.6应用能控性检验矩阵的方法证明状态反馈不改变系统的能控性。

然而，对以下系统应用能控性检验矩阵的方法证明状态反馈不改变系统的能控性。

然而，对以下系统01023131xxuyx=+=?

可以通过选择适当的状态反馈增益矩阵来改变闭环系统的能观性。

可以通过选择适当的状态反馈增益矩阵来改变闭环系统的能观性。

答：

答：

对于用能控性检验矩阵的方法证明状态反馈不改变系统的能控性，在题5.4中已经证明。

开环系统的能观性矩阵为031,20CACCA=由于能观性矩阵满秩，故系统是能观的。

设12Kkk=，引入状态反馈uKxv=+后，闭环系统的状态矩阵是120123AABKkk=?

闭环系统的能观性矩阵为012312CACkkCA=?

取20K=，则可得03100AC=?

该矩阵不是满秩的，故系统是不能观的。

这个例子说明了状态反馈的引入使得原来能观的系统变得不能观了。

5.7证明定理证明定理5.1.2。

证明：

证明：

先证能控性。

对任一输出反馈系统都可对应地构造等价的一个状态反馈系统。

由定理5.1.1知，状态反馈不改变系统的能控性，因而，输出反馈也不改变系统的能控性。

设被控系统的状态空间模型为：

0SxAxBuyCx=+=?

引入状态反馈后，闭环系统的状态空间模型为：

FS（）xABFCxBvyCx=+=?

系统和的能观矩阵分别为0SFS01nCCAQCA=?

，01（）（）FnCCABFCQCABFC=?

可以看出，（CABFC）每个行均可表为,TTTTCAC各行的线性组合，同理有是各行的线性组合，如此等等。

据此可以导出：

2（）CABFC2,（）TTTTTTCACACoForankQrankQ由于又可以看成为的输出反馈系统，因而有oSFSoorankQrankQF由以上两式可得oorankQrankQF=因此，系统完全能观测等价于完全能观测。

FS0S5.8采用状态反馈实现闭环极点任意配置的条件是什么？

采用状态反馈实现闭环极点任意配置的条件是什么？

答：

答：

采用状态反馈实现闭环极点任意配置的条件是，开环系统是能控的。

5.9采用状态反馈实现闭环极点任意配置，其状态反馈增益矩阵采用状态反馈实现闭环极点任意配置，其状态反馈增益矩阵K的行数和列数如何确定，计算方法有几种？

的行数和列数如何确定，计算方法有几种？

答：

答：

状态反馈增益矩阵K的行数是输入变量的个数，列数是状态变量的个数。

计算方法有：

1.直接法；2.变换法；3.利用爱克曼公式求解。

5.10为什么要进行极点配置？

解决系统极点配置问题的思路和步骤是什么？

为什么要进行极点配置？

解决系统极点配置问题的思路和步骤是什么？

答：

答：

对一个线性时不变系统，其稳定性和动态性能主要是由系统极点所决定，闭环极点在复平面的适当位置上就可以保证系统具有一定的性能。

因此，为了得到期望的系统性能，可以通过改变闭环系统极点位置的方式来实现，这就是极点配置的思想。

解决极点配置问题的思路如下：

1、要改变系统的行为，自然想到所考虑的系统应该是能控的。

因此，从能控系统入手来分析系统的求解问题；2、一般的能控系统也是很复杂的，为了求解问题，从最简单的能控系统开始，即从三阶的能控标准型模型出发分析极点配置问题的解，进而推广到阶能控标准型模型；n3、对一般的能控系统，设法将它化成等价的能控标准型模型，进而利用第2步的方法得到极点配置问题的解。

解决极点配置问题的具体方法和步骤如下：

（1）直接法：

1、检验系统的能控性。

如果系统是能控的，则继续第2步。

2、利用给定的期望闭环极点，可得到期望的闭环特征多项式为11211（）（）（）nnnnbb0b=+?

+3、系统矩阵ABK的特征多项式111det（）nnn0IABKaaa=+?

4、两个多项式相等即等号两边同次幂的系数相等，导出关于K的分量的一个线性方程组，求解该线性方程组，可得要求的增益矩阵1,nkk?

K。

（2）变换法：

1、检验系统的能控性。

如果系统是能控的，则继续第2步。

2、利用系统矩阵A的特征多项式111det（）nnn0IAaa=+?

a确定的值。

011,naaa?

3、确定将系统状态方程变换为能控标准形的变换矩阵T。

若给定的状态方程已经是能控标准形，那么TI=。

非奇异线性变换矩阵T可由下式决定：

1,（ccB,）TAAB=?

0b4、利用给定的期望闭环极点，可得到期望的闭环特征多项式为11211（）（）（）nnnnbb=+?

+5、确定极点配置状态反馈增益矩阵K：

00112211nnnnKbabababaT=?

5.11已知系统状态方程已知系统状态方程111011xxu=+=+?

计算状态反馈增益矩阵，使得闭环极点为计算状态反馈增益矩阵，使得闭环极点为2和和3，并画出反馈系统的结构图。

，并画出反馈系统的结构图。

答：

答：

由，得能控性矩阵为1101A=11B=12（,）11cABBAB=det（,）10cAB=所以系统是能控的。

由于211det（）2101IA=+系统的能控标准形矩阵对是0112A=?

，01B=?

故状态变换矩阵为：

1,（,）ccTABAB=?

01121211=1110=根据给定的期望闭环极点，可得闭环特征多项式为：

212（）（）

（2）（3）5=+=+6因此，状态反馈增益矩阵是57KT=125=结构图为2?

x1?

x2x1x5.12给定系统给定系统210011xxu=+=+?

（1）画出模拟结构图；）画出模拟结构图；

（2）画出单位阶跃响应曲线。

若动态性能不满足要求，可否任意配置闭环系统极点？

）画出单位阶跃响应曲线。

若动态性能不满足要求，可否任意配置闭环系统极点？

（3）若指定闭环极点为）若指定闭环极点为3和和3，求状态反馈增益矩阵，并画出单位阶跃响应曲线。

，求状态反馈增益矩阵，并画出单位阶跃响应曲线。

答：

答：

（1）模拟结构图2x?

-u2-2x1x1x?

（2）其单位阶跃响应曲线如图所示StepResponseTime（sec）Amplitude0123456700.050.10.150.20.250.30.350.40.450.5System:

gSettlingTime（sec）:

4.6System:

gRiseTime（sec）:

2.97系统的能控性矩阵为：

01（,）11cABBAB=而，故系统是能控的。

因此，若系统性能不满足要求，可以通过配置闭环系统极点来改善系统性能。

det（,）10cAB=（3）设状态反馈增益矩阵12Kkk=，可得（）IABK12211kk+=+2212det（）（3）22IABKkkk=+由指定的闭环极点3和，可得期望的闭环特征多项式为：

322（3）69+=+由此可得：

，即121,3kk=13K=极点配置后的闭环系统为：

210（）141xABKxBvxv=+=+?

它的单位阶跃响应曲线为：

StepResponseTime（sec）Amplitude00.511.522.500.020.040.060.080.10.12System:

gSettlingTime（sec）:

1.94System:

gRiseTime（sec）:

1.3对比两图可以发现，系统的动态性能大大改善。

5.13已知系统的传递函数为已知系统的传递函数为2

（1）（）（3sGsss+=+=）+，根据其能控标准形实现设计一个状态反馈控制器，将闭环极点配置在，根据其能控标准形实现设计一个状态反馈控制器，将闭环极点配置在2，2和和1处，并说明所得的闭环系统状态空间模型是否能观。

处，并说明所得的闭环系统状态空间模型是否能观。

答：

答：

由系统的传递函数2

（1）（）（3sGsss）+=+，可以得到系统的能控标准形为：

010000100031xxu=+?

110yx=设状态反馈增益矩阵123Kkkk=，则（）IABK12310013kkk=+3232det（）（3）1IABKkkk=+由指定的闭环极点2、和可得期望的闭环特征多项式：

21232

（2）

（1）58+=+4由此可得：

，即1234,8,2kkk=482K=。

因此，要设计的状态反馈控制器是482ux=极点配置后的闭环系统为：

010000104851xxv=+?

110yx=该系统的能观性矩阵为：

2110011484oCACCACA=det（）0oAC=因此所得的闭环系统状态空间模型是不能观的。

5.14已知系统的传递函数为已知系统的传递函数为

（1）

（2）（）

（1）

（2）（3ssGssss+=+=）+试问能否用状态反馈将闭环系统的传递函数变为试问能否用状态反馈将闭环系统的传递函数变为1（）

（2）（3csGsss=）+若有可能，试给出相应的状态反馈控制器，并画出控制系统结构图。

若有可能，试给出相应的状态反馈控制器，并画出控制系统结构图。

答：

答：

能够用状态反馈将闭环系统的传递函数变为1（）

（2）（3csGsss）=+。

根据原系统的传递函数可以得到能控标准形。

由定理5.1.3，对能控的单输入单输出系统，只要不发生零极点相消的现象，状态反馈就不能改变零点。

因此我们只能用状态反馈把原系统变换为2

（1）

（2）（）

（2）（3cssGsss）+=+即将闭环系统极点配置在、和223的位置上。

原系统的状态方程为：

010000106521xxu=+?

211yx=设状态反馈增益矩阵123Kkkk=，则（）IABK123100165kkk2=+32321