东南大学统计信号处理实验一.doc

东南大学统计信号处理实验一.doc

《东南大学统计信号处理实验一.doc》由会员分享，可在线阅读，更多相关《东南大学统计信号处理实验一.doc（15页珍藏版）》请在冰豆网上搜索。

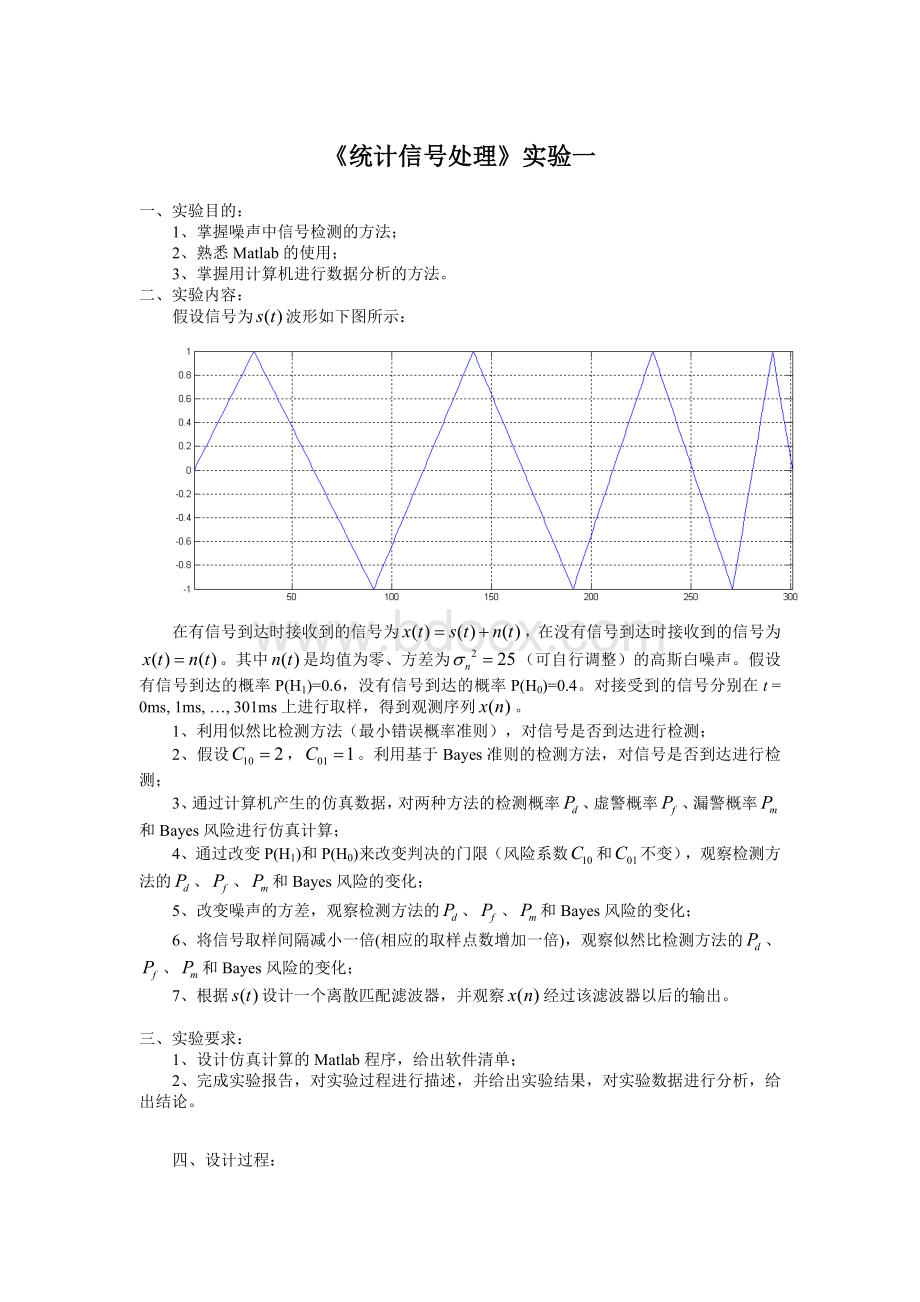
《统计信号处理》实验一

一、实验目的：

1、掌握噪声中信号检测的方法；

2、熟悉Matlab的使用；

3、掌握用计算机进行数据分析的方法。

二、实验内容：

假设信号为波形如下图所示：

在有信号到达时接收到的信号为，在没有信号到达时接收到的信号为。

其中是均值为零、方差为（可自行调整）的高斯白噪声。

假设有信号到达的概率P（H1）=0.6，没有信号到达的概率P（H0）=0.4。

对接受到的信号分别在t=0ms,1ms,…,301ms上进行取样，得到观测序列。

1、利用似然比检测方法（最小错误概率准则），对信号是否到达进行检测；

2、假设，。

利用基于Bayes准则的检测方法，对信号是否到达进行检测；

3、通过计算机产生的仿真数据，对两种方法的检测概率、虚警概率、漏警概率和Bayes风险进行仿真计算；

4、通过改变P（H1）和P（H0）来改变判决的门限（风险系数和不变），观察检测方法的、、和Bayes风险的变化；

5、改变噪声的方差，观察检测方法的、、和Bayes风险的变化；

6、将信号取样间隔减小一倍（相应的取样点数增加一倍），观察似然比检测方法的、、和Bayes风险的变化；

7、根据设计一个离散匹配滤波器，并观察经过该滤波器以后的输出。

三、实验要求：

1、设计仿真计算的Matlab程序，给出软件清单；

2、完成实验报告，对实验过程进行描述，并给出实验结果，对实验数据进行分析，给出结论。

四、设计过程：

1、产生信号s（t），n（t），x（t），t=0ms,1ms,…,301ms；其中：

2、根据定义似然比函数，门限，如果，则判定；否则，判定。

这就是似然比检测准则。

假设似然比为x，在某取样率的条件下，假设得到的随机变量分布为x1，x2，…，xN。

则没有信号时的概率密度函数为：

有信号时的概率密度函数为：

由此可以得到似然比函数为：

相应的似然比判决准则为：

>时判定；否则，判定。

或：

时判定；否则，判定。

其中，是判决门限，本题中=。

3、Bayes判决准则如下，风险函数是各个概率的线形组合：

很多情况下，可以令，即正确判断是不具有风险的，此时判决公式为：

如果，判为；否则，判为。

本题中，，故判决门限为。

4、做M=100000次统计，在有信号到达的情况下，即，每次出现'signalisdetected'时，检测到信号的次数n0加1，出现'nosignal'时，没有检测到信号的次数n1加1;在没有信号到达的情况下，即，每次出现'signalisdetected'时，检测到信号的次数n2加1，出现'nosignal'时，没有检测到信号的次数n3加1。

则：

检测概率=n0/M；虚警概率=n2/M；漏警概率=n1/M；

Bayes风险==

5、用相同的方法，通过改变判决的门限，观察检测方法的、、和Bayes风险的变化。

6、用相同的方法，通过改变噪声的方差，观察检测方法的、、和Bayes风险的变化。

7、设计匹配滤波器h（t）=c*s（T-t），通过使待检测信号x（t）经过匹配滤波器，即和h（t）进行卷积，得到滤波以后的输出X（t）。

五、实验结果及分析：

1、利用似然比检测方法（最小错误概率准则），对信号是否到达进行检测。

实验得到的波形如下：

对302个抽样点进行了五次检测，得到结果如下：

检测到信号的次数C

平均值

275

257

276

272

267

270

分析：

可能由于高斯白噪声的影响较大，故有些信号没有被检测出来。

2、假设，。

利用基于Bayes准则的检测方法，对信号是否到达进行检测。

同样地，对302个抽样点进行了五次检测，得到结果如下：

检测到信号的次数C

平均值

253

236

244

236

243

242

分析：

比较可得，在本题设定的风险系数下，基于Bayes准则的检测方法没有似然比检测方法可靠。

3、通过计算机产生的仿真数据，对两种方法的检测概率、虚警概率、漏警概率和Bayes风险进行仿真计算。

采用似然比检测方法得到的仿真结果如下：

pd=0.8855，pf=0.2140，pm=0.1145，r=0.5424。

利用基于Bayes准则的检测方法得到的仿真结果如下：

Pd=0.8032，Pf=0.1264，Pm=0.1968，r=0.4496。

比较可得：

采用似然比检测方法得到的检测概率较大，漏警概率较小；基于Bayes准则的检测方法得到的虚警概率较小，风险系数较小。

4、通过改变P（H1）和P（H0）来改变判决的门限（风险系数和不变），观察检测方法的、、和Bayes风险的变化。

（1）似然比检测方法

Bayes风险

0.8855

0.2140

0.1145

0.5424

0.8425

0.1581

0.1576

0.4738

0.7899

0.1162

0.2101

0.4424

0.4595

0.0176

0.5405

0.5758

由表格可以看出当门限升高时检测概率降低，虚警概率降低，漏警概率升高，bayes风险值变化不大。

没有信号到达的概率越高，检测概率和虚警概率就越低，漏警概率越高，实际值符合理论分析。

（2）基于Bayes准则的检测方法

Bayes风险

0.8032

0.1264

0.1968

0.4496

0.7464

0.0886

0.2536

0.4309

0.6748

0.0610

0.3252

0.4472

0.3284

0.0071

0.6716

0.6858

由表格可以看出当门限升高时检测概率降低，虚警概率降低，漏警概率升高。

没有信号到达的概率越高，检测概率和虚警概率就越低，漏警概率越高，实际值符合理论分析。

由于虚警概率降低，并且相乘得出风险时前面系数较大，所以风险先降低，后来由于漏警概率的升高已经大过于虚警概率对风险的影响，所以后来风险又升高。

5、改变噪声的方差，观察检测方法的、、和Bayes风险的变化。

（1）似然比检测方法

Bayes风险

9

0.9540

0.0599

0.0360

0.1559

25

0.8855

0.2140

0.1145

0.5424

36

0.8582

0.2785

0.1418

0.6988

49

0.8393

0.3331

0.1607

0.8268

（2）基于Bayes准则的检测方法

Bayes风险

9

0.9432

0.0301

0.0568

0.1170

25

0.8032

0.1264

0.1968

0.4496

36

0.7448

0.1057

0.2552

0.4666

49

0.6949

0.1138

0.3051

0.5327

由表格可以看出当噪声方差增大时，两种检测方法得到的检测概率均降低，虚警概率均升高，漏警概率均升高，风险值均增大。

这是因为噪声方差越大，对信号的干扰越大，检测信号越困难，即两种方法的可靠性越差。

6、将信号取样间隔减小一倍（相应的取样点数增加一倍），观察似然比检测方法的、、和Bayes风险的变化。

之前的结果：

pd=0.8855，pf=0.2140，pm=0.1145，r=0.5424

取样点数增加一倍后的结果为：

pd=0.9397，pf=0.1007，pm=0.0603，r=0.2617

比较可得，取样点数增加一倍后，检测可信度大为提高。

7、根据设计一个离散匹配滤波器，并观察经过该滤波器以后的输出。

设计的滤波器波形如下：

有信号和无信号状态下的x（t）经过滤波器后的输出分别如下：

分析：

当t=300时，有信号时的输出值达到最大，无信号时的输出值为0，这说明匹配滤波器对有用信号分量有放大作用，对干扰信号有抑制作用，有利于信号的检测。

源程序：

%1

%产生信号s（t）,n（t）,x（t）

t=0:

29;

s1=t/30;

t=30:

89;

s2=-t/30+2;

t=90:

139;

s3=t/25-4.6;

t=140:

189;

s4=-t/25+6.6;

t=190:

229;

s5=t/20-10.5;

t=230:

269;

s6=-t/20+12.5;

t=270:

289;

s7=t/10-28;

t=290:

301;

s8=-t/10+30;

s=[s1s2s3s4s5s6s7s8];

p0=0.4;

p1=0.6;

fort=1:

302

n=5.*randn（1,302）;

x=s+n;

figure

（1）;

subplot（3,1,1）;grid;plot（s）;axis（[0,301,-1,1]）;xlabel（'t/ms'）;ylabel（'s（t）'）;

subplot（3,1,2）;grid;plot（n）;axis（[0,301,-20,20]）;xlabel（'t/ms'）;ylabel（'n（t）'）;

subplot（3,1,3）;grid;plot（x）;axis（[0,301,-20,20]）;xlabel（'t/ms'）;ylabel（'x（t）'）;

%利用似然比检测方法检测信号是否到达

x1=x.*s;

x2=s.*s;

ifsum（x1）>25*log（p0/p1）+0.5*sum（x2）

count（t）=1;

'signalisdetected'

else

count（t）=0;

'nosignal'

end;

end;

C=sum（count）;

C

%2

%产生信号s（t）,n（t）,x（t）

t=0:

29;

s1=t/30;

t=30:

89;

s2=-t/30+2;

t=90:

139;

s3=t/25-4.6;

t=140:

189;

s4=-t/25+6.6;

t=190:

229;

s5=t/20-10.5;

t=230:

269;

s6=-t/20+12.5;

t=270:

289;

s7=t/10-28;

t=290:

301;

s8=-t/10+30;

s=[s1s2s3s4s5s6s7s8];

p0=0.4;

p1=0.6;

fort=1:

302

n=5.*randn（1,302）;

x=s+n;

figure

（1）;

subplot（3,1,1）;grid;plot（s）;axis（[0,301,-1,1]）;xlabel（'t/ms'）;ylabel（'s（t）'）;

subplot（3,1,2）;grid;plot（n）;axis（[0,301,-20,20]）;xlabel（'t/ms'）;ylabel（'n（t）'）;

subplot（3,1,3）;grid;plot（x）;axis（[0,301,-20,20]）;xlabel（'t/ms'）;ylabel（'x（t）'）;

%利用基于Bayes准则的检测方法检测信号是否到达

x1=x.*s;

x2=s.*s;

ifsum（x1）>25*log（4/3）+0.5*sum（x2）

count（t）=1;

'signalisdetected'

else

count（t）=0;

'nosignal'

end;

end;

C=sum（count）;

C

%3%4%5

p0=0.4;

p1=0.6;//修改p0、p1以实现第四问

c10=2;

c01=1;

n0=0;n1=0;n2=0;n3=0;

M=100000;

fori=1:

100001

t=0:

29;

s1=t/30;

t=30:

89;

s2=-t/30+2;

t=90:

139;

s3=t/25-4.6;

t=140:

189;

s4=-t/25+6.6;

t=190:

229;

s5=t/20-10.5;

t=230:

269;

s6=-t/20+12.5;

t=270:

289;

s7=t/10-28;

t=290:

301;

s8=-t/10+30;

s=[s1s2s3s4s5s6s7s8];

n=5.*randn（1,302）;//修改系数以实现第五问

x=s+n;

%有信号到达，利用似然比检测方法检测信号是否到达

x1=x.*s;

x2=s.*s;

ifsum（x1）>25*log（p0/p1）+0.5*sum（x2）//修改系数以实现第五问

n0=n0+1;

'signalisdetected'

else

n1=n1+1;

'nosignal'

end;

end;

fori=1:

100001

n=5.*randn（1,302）;

x=n;

%没有信号到达，利用似然比检测方法检测信号是否到达

x1=x.*s;

x2=s.*s;

ifsum（x1）>25*log（p0/p1）+0.5*sum（x2）

n2=n2+1;

'signalisdetected'

else

n3=n3+1;

'nosignal'

end;

end;

pd1=n0/M;

pf1=n2/M;

pm1=n1/M;

r1=c01*pm1+c10*pf1;

pd1

pf1

pm1

r1

fori=1:

100001

t=0:

29;

s1=t/30;

t=30:

89;

s2=-t/30+2;

t=90:

139;

s3=t/25-4.6;

t=140:

189;

s4=-t/25+6.6;

t=190:

229;

s5=t/20-10.5;

t=230:

269;

s6=-t/20+12.5;

t=270:

289;

s7=t/10-28;

t=290:

301;

s8=-t/10+30;

s=[s1s2s3s4s5s6s7s8];

n=5.*randn（1,302）;%修改系数以实现第五问

x=s+n;

%有信号到达，利用基于Bayes准则的检测方法检测信号是否到达

x1=x.*s;

x2=s.*s;

ifsum（x1）>25*log（4/3）+0.5*sum（x2）%修改系数以实现第五问

n0=n0+1;

'signalisdetected'

else

n1=n1+1;

'nosignal'

end;

end;

fori=1:

100001

n=5.*randn（1,302）;%修改系数以实现第五问

x=n;

%没有信号到达，利用基于Bayes准则的检测方法检测信号是否到达

x1=x.*s;

x2=s.*s;

ifsum（x1）>25*log（4/3）+0.5*sum（x2）%修改系数以实现第五问

n2=n2+1;

'signalisdetected'

else

n3=n3+1;

'nosignal'

end;

end;

pd2=n0/M;

pf2=n2/M;

pm2=n1/M;

r2=c01*pm2+c10*pf2;

pd2

pf2

pm2

r2

%6

%产生信号s（t）,n（t）,x（t）

t=0:

0.5:

29.5;

s1=t/30;

t=30:

0.5:

89.5;

s2=-t/30+2;

t=90:

0.5:

139.5;

s3=t/25-4.6;

t=140:

0.5:

189.5;

s4=-t/25+6.6;

t=190:

0.5:

229.5;

s5=t/20-10.5;

t=230:

0.5:

269.5;

s6=-t/20+12.5;

t=270:

0.5:

289.5;

s7=t/10-28;

t=290:

0.5:

301;

s8=-t/10+30;

s=[s1s2s3s4s5s6s7s8];

p0=0.4;

p1=0.6;

fort=1:

302*2

n=5.*randn（1,302*2）;

x=s+n;

figure

（1）;

subplot（3,1,1）;grid;plot（s）;axis（[0,301,-1,1]）;xlabel（'t/ms'）;ylabel（'s（t）'）;

subplot（3,1,2）;grid;plot（n）;axis（[0,301,-20,20]）;xlabel（'t/ms'）;ylabel（'n（t）'）;

subplot（3,1,3）;grid;plot（x）;axis（[0,301,-20,20]）;xlabel（'t/ms'）;ylabel（'x（t）'）;

%有信号到达，利用似然比检测方法检测信号是否到达

x1=x.*s;

x2=s.*s;

ifsum（x1）>25*log（p0/p1）+0.5*sum（x2）

n0=n0+1;

'signalisdetected'

else

n1=n1+1;

'nosignal'

end;

end;

fori=1:

100001

n=5.*randn（1,302）;

x=n;

%没有信号到达，利用似然比检测方法检测信号是否到达

x1=x.*s;

x2=s.*s;

ifsum（x1）>25*log（p0/p1）+0.5*sum（x2）

n2=n2+1;

'signalisdetected'

else

n3=n3+1;

'nosignal'

end;

end;

pd1=n0/M;

pf1=n2/M;

pm1=n1/M;

r1=c01*pm1+c10*pf1;

pd1

pf1

pm1

r1

%7

t=0:

29;

s1=t/30;

t=30:

89;

s2=-t/30+2;

t=90:

139;

s3=t/25-4.6;

t=140:

189;

s4=-t/25+6.6;

t=190:

229;

s5=t/20-10.5;

t=230:

269;

s6=-t/20+12.5;

t=270:

289;

s7=t/10-28;

t=290:

301;

s8=-t/10+30;

s=[s1s2s3s4s5s6s7s8];

fori=1:

301

h（i）=s（302-i）;

end

n=5.*randn（1,302）;

x1=s+n;

x2=n;

figure

（1）;

subplot（2,1,1）;plot（s）;grid;axis（[0,301,-1,1]）;xlabel（'t/ms'）;ylabel（'s（t）'）;

subplot（2,1,2）;plot（h）;grid;axis（[0,301,-1,1]）;xlabel（'t/ms'）;ylabel（'匹配滤波器h（t）'）;

X1=conv（h,x1）;

X2=conv（h,x2）;

figure

（2）;

subplot（2,1,1）;plot（x1）;grid;axis（[0,301,-20,20]）;xlabel（'t/ms'）;ylabel（'x（t）'）;title（'有信号'）

subplot（2,1,2）;plot（X1）;grid;axis（[0,650,-150,150]）;xlabel（'t/ms'）;ylabel（'输出信号'）;

figure（3）;

subplot（2,1,1）;plot（x2）;grid;axis（[0,301,-20,20]）;xlabel（'t/ms'）;ylabel（'x（t）'）;title（'无信号'）

subplot（2,1,2）;plot（X2）;grid;axis（[0,650,-150,150]）;xlabel（'t/ms'）;ylabel（'输出信号'）;