中考特殊平行四边形证明及计算经典习题及答案讲解学习.docx

中考特殊平行四边形证明及计算经典习题及答案讲解学习.docx

《中考特殊平行四边形证明及计算经典习题及答案讲解学习.docx》由会员分享，可在线阅读，更多相关《中考特殊平行四边形证明及计算经典习题及答案讲解学习.docx（52页珍藏版）》请在冰豆网上搜索。

中考特殊平行四边形证明及计算经典习题及答案讲解学习

中考特殊平行四边形证明及计算经典习题及答案

DSE金牌数学专题系列经典专题系列

初中数学中考特殊四边形证明及计算

一．解答题

1．

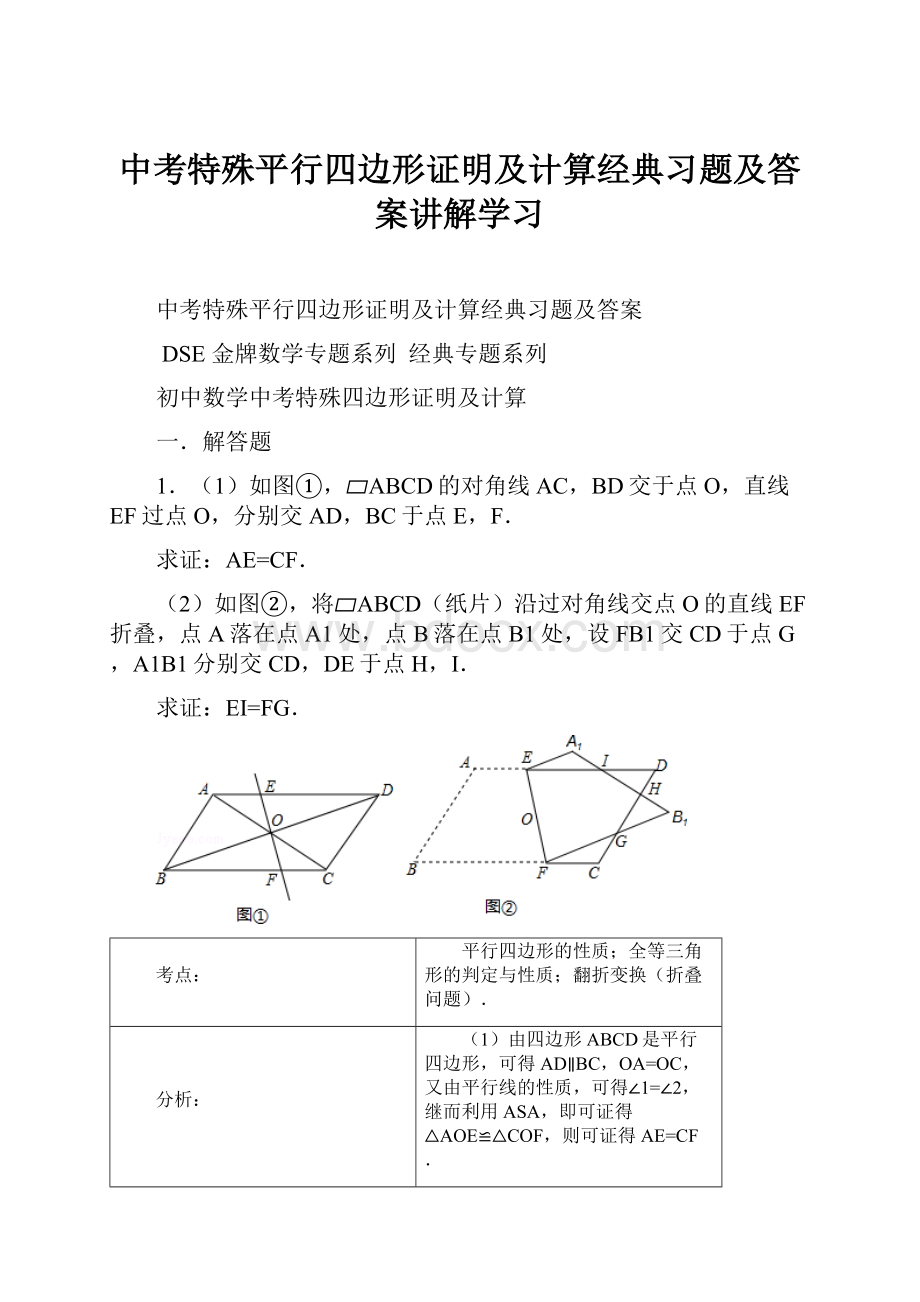
（1）如图①，▱ABCD的对角线AC，BD交于点O，直线EF过点O，分别交AD，BC于点E，F．

求证：

AE=CF．

（2）如图②，将▱ABCD（纸片）沿过对角线交点O的直线EF折叠，点A落在点A1处，点B落在点B1处，设FB1交CD于点G，A1B1分别交CD，DE于点H，I．

求证：

EI=FG．

考点：

平行四边形的性质；全等三角形的判定与性质；翻折变换（折叠问题）．

分析：

（1）由四边形ABCD是平行四边形，可得AD∥BC，OA=OC，又由平行线的性质，可得∠1=∠2，继而利用ASA，即可证得△AOE≌△COF，则可证得AE=CF．

（2）根据平行四边形的性质与折叠性质，易得A1E=CF，∠A1=∠A=∠C，∠B1=∠B=∠D，继而可证得△A1IE≌△CGF，即可证得EI=FG．

解答：

证明：

（1）∵四边形ABCD是平行四边形，

∴AD∥BC，OA=OC，

∴∠1=∠2，

在△AOE和△COF中，

，∴△AOE≌△COF（ASA），∴AE=CF；

（2）∵四边形ABCD是平行四边形，∴∠A=∠C，∠B=∠D，由

（1）得AE=CF，

由折叠的性质可得：

AE=A1E，∠A1=∠A，∠B1=∠B，

∴A1E=CF，∠A1=∠A=∠C，∠B1=∠B=∠D，又∵∠1=∠2，∴∠3=∠4，∵∠5=∠3，∠4=∠6，∴∠5=∠6，在△A1IE与△CGF中，

，∴△A1IE≌△CGF（AAS），∴EI=FG．

点评：

此题考查了平行四边形的性质、折叠的性质以及全等三角形的判定与性质．此题难度适中，注意掌握折叠前后图形的对应关系，注意数形结合思想的应用．

2．在△ABC中，AB=AC，点P为△ABC所在平面内一点，过点P分别作PE∥AC交AB于点E，PF∥AB交BC于点D，交AC于点F．若点P在BC边上（如图1），此时PD=0，可得结论：

PD+PE+PF=AB．

请直接应用上述信息解决下列问题：

当点P分别在△ABC内（如图2），△ABC外（如图3）时，上述结论是否成立？

若成立，请给予证明；若不成立，PD，PE，PF与AB之间又有怎样的数量关系，请写出你的猜想，不需要证明．

考点：

平行四边形的性质．718351

专题：

探究型．

分析：

在图2中，因为四边形PEAF为平行四边形，所以PE=AF，又三角形FDC为等腰三角形，所以FD=PF+PD=FC，即PE+PD+PF=AC=AB，在图3中，PE=AF可证，FD=PF﹣PD=CF，即PF﹣PD+PE=AC=AB．

解答：

解：

图2结论：

PD+PE+PF=AB．

证明：

过点P作MN∥BC分别交AB，AC于M，N两点，

∵PE∥AC，PF∥AB，

∴四边形AEPF是平行四边形，

∵MN∥BC，PF∥AB

∴四边形BDPM是平行四边形，

∴AE=PF，∠EPM=∠ANM=∠C，

∵AB=AC，

∴∠EMP=∠B，

∴∠EMP=∠EPM，

∴PE=EM，

∴PE+PF=AE+EM=AM．

∵四边形BDPM是平行四边形，

∴MB=PD．

∴PD+PE+PF=MB+AM=AB，

即PD+PE+PF=AB．

图3结论：

PE+PF﹣PD=AB．

点评：

此题主要考查了平行四边形的性质，难易程度适中，读懂信息，把握规律是解题的关键．

3．如图，△ABC是等边三角形，点D是边BC上的一点，以AD为边作等边△ADE，过点C作CF∥DE交AB于点F．

（1）若点D是BC边的中点（如图①），求证：

EF=CD；

（2）在

（1）的条件下直接写出△AEF和△ABC的面积比；

（3）若点D是BC边上的任意一点（除B、C外如图②），那么

（1）中的结论是否仍然成立？

若成立，请给出证明；若不成立，请说明理由．

考点：

平行四边形的判定与性质；全等三角形的判定与性质；等边三角形的性质．718351

专题：

证明题．

分析：

（1）根据△ABC和△AED是等边三角形，D是BC的中点，ED∥CF，求证△ABD≌△CAF，进而求证四边形EDCF是平行四边形即可；

（2）在

（1）的条件下可直接写出△AEF和△ABC的面积比；

（3）根据ED∥FC，结合∠ACB=60°，得出∠ACF=∠BAD，求证△ABD≌△CAF，得出ED=CF，进而求证四边形EDCF是平行四边形，即可证明EF=DC．

解答：

（1）证明：

∵△ABC是等边三角形，D是BC的中点，

∴AD⊥BC，且∠BAD=

∠BAC=30°，

∵△AED是等边三角形，

∴AD=AE，∠ADE=60°，

∴∠EDB=90°﹣∠ADE=90°﹣60°=30°，

∵ED∥CF，

∴∠FCB=∠EDB=30°，∵∠ACB=60°，∴∠ACF=∠ACB﹣∠FCB=30°，

∴∠ACF=∠BAD=30°，在△ABD和△CAF中，

，

∴△ABD≌△CAF（ASA），∴AD=CF，∵AD=ED，

∴ED=CF，又∵ED∥CF，∴四边形EDCF是平行四边形，∴EF=CD．

（2）解：

△AEF和△ABC的面积比为：

1：

4；

（3）解：

成立．

理由如下：

∵ED∥FC，

∴∠EDB=∠FCB，

∵∠AFC=∠B+∠BCF=60°+∠BCF，∠BDA=∠ADE+∠EDB=60°+∠EDB

∴∠AFC=∠BDA，

在△ABD和△CAF中，

∴△ABD≌△CAF（AAS），

∴AD=FC，

∵AD=ED，

∴ED=CF，

又∵ED∥CF，

∴四边形EDCF是平行四边形，

∴EF=DC．

点评：

此题主要考查学生对平行四边形的判定和性质、全等三角形的判定和性质、等边三角形的性质的理解和掌握．此题涉及到的知识点较多，综合性较强，难度较大．

4．如图，在菱形ABCD中，AB=10，∠BAD=60度．点M从点A以每秒1个单位长的速度沿着AD边向点D移动；设点M移动的时间为t秒（0≤t≤10）．

（1）点N为BC边上任意一点，在点M移动过程中，线段MN是否一定可以将菱形分割成面积相等的两部分并说明理由；

（2）点N从点B（与点M出发的时刻相同）以每秒2个单位长的速度沿着BC边向点C移动，在什么时刻，梯形ABNM的面积最大并求出面积的最大值；

（3）点N从点B（与点M出发的时刻相同）以每秒a（a≥2）个单位长的速度沿着射线BC方向（可以超越C点）移动，过点M作MP∥AB，交BC于点P．当△MPN≌△ABC时，设△MPN与菱形ABCD重叠部分的面积为S，求出用t表示S的关系式，井求当S=0时的值．

考点：

菱形的性质；二次函数的最值；全等三角形的性质．718351

专题：

压轴题．

分析：

（1）菱形被分割成面积相等的两部分，那么分成的两个梯形的面积相等，而两个梯形的高相等，只需上下底的和相等即可．

（2）易得菱形的高，那么用t表示出梯形的面积，用t的最值即可求得梯形的最大面积．

（3）易得△MNP的面积为菱形面积的一半，求得不重合部分的面积，让菱形面积的一半减去即可．

解答：

解：

（1）设：

BN=a，CN=10﹣a（0≤a≤10）

因为，点M从点A以每秒1个单位长的速度沿着AD边向点D移动，点M移动的时间为t秒（0≤t≤10）

所以，AM=1×t=t（0≤t≤10），MD=10﹣t（0≤t≤10）．

所以，梯形AMNB的面积=（AM+BN）×菱形高÷2=（t+a）×菱形高÷2；

梯形MNCD的面积=（MD+NC）×菱形高÷2=[（10﹣t）+（10﹣a）]×菱形高÷2

当梯形AMNB的面积=梯形MNCD的面积时，

即t+a=10，（0≤t≤10），（0≤a≤10）

所以，当t+a=10，（0≤t≤10），（0≤a≤10）时，可出现线段MN一定可以将菱形分割成面积相等的两部分．

（2）点N从点B以每秒2个单位长的速度沿着BC边向点C移动，设点N移动的时间为t，可知0≤t≤5，

因为AB=10，∠BAD=60°，所以菱形高=5

，

AM=1×t=t，BN=2×t=2t．

所以梯形ABNM的面积=（AM+BN）×菱形高÷2=3t×5

×

=

t（0≤t≤5）．

所以当t=5时，梯形ABNM的面积最大，其数值为

．

（3）当△MPN≌△ABC时，

则△ABC的面积=△MPN的面积，则△MPN的面积为菱形面积的一半为25

；

因为要全等必有MN∥AC，

∴N在C点外，所以不重合处面积为

×（at﹣10）2×

∴重合处为S=25

﹣

，

当S=0时，即PM在CD上，

∴a=2．

点评：

本题考查了菱形以及相应的三角函数的性质，注意使用两条平行线间的距离相等等条件．

5．如图，在下列矩形ABCD中，已知：

AB=a，BC=b（a＜b），假定顶点在矩形边上的菱形叫做矩形的内接菱形，现给出（Ⅰ）、（Ⅱ）、（Ⅲ）三个命题：

命题（Ⅰ）：

图①中，若AH=BG=AB，则四边形ABGH是矩形ABCD的内接菱形；

命题（Ⅱ）：

图②中，若点E、F、G和H分别是AB、BC、CD和DE的中点，则四边形EFGH是矩形ABCD的内接菱形；

命题（Ⅲ）：

图③中，若EF垂直平分对角线AC，变BC于点E，交AD于点F，交AC于点O，则四边形AECF是矩形ABCD的内接菱形．

请解决下列问题：

（1）命题（Ⅰ）、（Ⅱ）、（Ⅲ）都是真命题吗？

请你在其中选择一个，并证明它是真命题或假命题；

（2）画出一个新的矩形内接菱形（即与你在

（1）中所确认的，但不全等的内接菱形）．

（3）试探究比较图①，②，③中的四边形ABGH、EFGH、AECF的面积大小关系．

考点：

菱形的判定与性质；全等三角形的判定与性质；线段垂直平分线的性质；三角形中位线定理；矩形的性质；命题与定理．718351

分析：

（1）①先证明是平行四边形，再根据一组邻边相等证明；

②根据三角形中位线定理得到四条边都相等；

③先根据三角形全等证明是平行四边形，再根据对角线互相垂直证明是菱形；

（2）先作一条对角线，在作出它的垂直平分线分别与矩形的边相交，连接四个交点即可．

（3）分别表示出三个菱形的面积，根据边的关系即可得出图

（1）图

（2）的面积都小于图（3）的面积；根据a与b的大小关系，分a＞2b，a=2b和a＜2b三种情况讨论．

解答：

解：

（1）都是真命题；

若选（Ⅰ）证明如下：

∵矩形ABCD，

∴AD∥BC，

∵AH=BG，

∴四边形ABGH是平行四边形，

∴AB=HG，

∴AB=HG=AH=BG，

∴四边形ABGH是菱形；

若选（Ⅱ），证明如下：

∵矩形ABCD，

∴AB=CD，AD=BC，

∠A=∠B=∠C=∠D=90°，

∵E、F、G、H是中点，

∴AE=BE=CG=DG，AH=HD=BF=FC，

∴△AEH≌△BEF≌△DGH≌△GCF，

∴EF=FG=GH=HE，

∴四边形EFGH是菱形；

若选（Ⅲ），证明如下

∵EF垂直平分AC，

∴FA=FC，EA=EC，

又∵矩形ABCD，

∴AD∥BC，

∴∠FAC=∠ECA，

在△AOF和△COE中，

，

∴△ADF≌△COE（SAS）

∴AF=CE，

∴AF=FC=CE=EA，

∴四边形AECF是菱形；

（2）如图4所示：

AH=CF，EG垂直平分对角线FH，四边形HEFG是菱形；

（3）SABGH=a2，

SEFGH=

ab，

S菱形AECF=

，

∵

﹣a2=

=

＞0（b＞a）

∴S菱形AECF＞SABGH．

∵

﹣

ab=

=

=

＞0，

∴S菱形AECF＞SEFGH．

∵a2﹣

ab=a（a﹣

b）

∴当a＞

b，即0＜b＜2a时，S菱形ABGH＞S菱形EFGH；

当a=

b，即b=2a时，S菱形ABGH=S菱形EFGH；

当a＜

b，即b＞a时，S菱形ABGH＜S菱形EFGH．

综上所述：

当O＜b＜2a时，SEFGH＜SABGH＜S菱形AECF．

当b=2a时，SEFGH=SABGH＜S菱形AECF．

当b＞2a时SABGH＜SEFGH＜S菱形AECF．

点评：

本题主要考查了菱形的判定与性质，三角形中位线定理，全等三角形的判定与性质以及矩形的性质等知识点．注意第（3）题需要分类讨论，以防错解．

6．在平行四边形ABCD中，∠BAD的平分线交直线BC于点E，交直线DC的延长线于点F，以EC、CF为邻边作平行四边形ECFG．

（1）如图1，证明平行四边形ECFG为菱形；

（2）如图2，若∠ABC=90°，M是EF的中点，求∠BDM的度数；

（3）如图3，若∠ABC=120°，请直接写出∠BDG的度数．

考点：

菱形的判定与性质；全等三角形的判定与性质；等腰直角三角形；平行四边形的性质；正方形的判定与性质．718351

分析：

（1）平行四边形的性质可得AD∥BC，AB∥CD，再根据平行线的性质证明∠CEF=∠CFE，根据等角对等边可得CE=CF，再有条件四边形ECFG是平行四边形，可得四边形ECFG为菱形；

（2）首先证明四边形ECFG为正方形，再证明△BME≌△DMC可得DM=BM，∠DMC=∠BME，再根据∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°可得到∠BDM的度数；

（3）分别连接GB、GC，求证四边形CEGF是平行四边形，再求证△ECG是等边三角形．由AD∥BC及AF平分∠BAD可得∠BAE=∠AEB，求证△BEG≌△DCG，然后即可求得答案．

解答：

解：

（1）证明：

∵AF平分∠BAD，

∴∠BAF=∠DAF，

∵四边形ABCD是平行四边形，

∴AD∥BC，AB∥CD，

∴∠DAF=∠CEF，∠BAF=∠CFE，

∴∠CEF=∠CFE，

∴CE=CF，

又∵四边形ECFG是平行四边形，

∴四边形ECFG为菱形．

（2）如图，连接BM，MC，

∵∠ABC=90°，四边形ABCD是平行四边形，

∴四边形ABCD是矩形，

又由

（1）可知四边形ECFG为菱形，

∠ECF=90°，

∴四边形ECFG为正方形．

∵∠BAF=∠DAF，

∴BE=AB=DC，

∵M为EF中点，

∴∠CEM=∠ECM=45°，

∴∠BEM=∠DCM=135°，

在△BME和△DMC中，

∵

，

∴△BME≌△DMC（SAS），

∴MB=MD，

∠DMC=∠BME．

∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°，

∴△BMD是等腰直角三角形，

∴∠BDM=45°；

（3）∠BDG=60°，

延长AB、FG交于H，连接HD．

∵AD∥GF，AB∥DF，

∴四边形AHFD为平行四边形，

∵∠ABC=120°，AF平分∠BAD，

∴∠DAF=30°，∠ADC=120°，∠DFA=30°，

∴△DAF为等腰三角形，

∴AD=DF，

∴平行四边形AHFD为菱形，

∴△ADH，△DHF为全等的等边三角形，

∴DH=DF，∠BHD=∠GFD=60°，

∵FG=CE，CE=CF，CF=BH，

∴BH=GF，

在△BHD与△GFD中，

∵

，

∴△BHD≌△GFD（SAS），

∴∠BDH=∠GDF

∴∠BDG=∠BDH+∠HDG=∠GDF+∠HDG=60°．

点评：

此题主要考查平行四边形的判定方法，全等三角形的判定与性质，等边三角形的判定与性质，菱形的判定与性质等知识点，应用时要认真领会它们之间的联系与区别，同时要根据条件合理、灵活地选择方法．

7．在△ABC中，∠BAC=90°，AB=AC，若点D在线段BC上，以AD为边长作正方形ADEF，如图1，易证：

∠AFC=∠ACB+∠DAC；

（1）若点D在BC延长线上，其他条件不变，写出∠AFC、∠ACB、∠DAC的关系，并结合图2给出证明；

（2）若点D在CB延长线上，其他条件不变，直接写出∠AFC、∠ACB、∠DAC的关系式．

考点：

正方形的性质；全等三角形的判定与性质；等腰三角形的性质．718351

专题：

几何综合题．

分析：

（1）∠AFC、∠ACB、∠DAC的关系为：

∠AFC=∠ACB﹣∠DAC，理由为：

由四边形ADEF为正方形，得到AD=AF，且∠FAD为直角，得到∠BAC=∠FAD，等式左右两边都加上∠CAD得到∠BAD=∠CAF，再由AB=AC，AD=AF，利用SAS可得出三角形ABD与三角形ACF全等，根据全等三角形的对应角相等可得出∠AFC=∠ADB，又∠ACB为三角形ACD的外角，利用外角的性质得到∠ACB=∠ADB+∠DAC，变形后等量代换即可得证；

（2）∠AFC、∠ACB、∠DAC的关系式是∠AFC+∠ACB+∠DAC=180°，可以根据∠DAF=∠BAC=90°，等号两边都减去∠BAF，可得出∠DAB=∠FAC，再由AD=AF，AB=AC，利用SAS证明三角形ABD与三角形AFC全等，由全等三角形的对应角相等可得出∠AFC=∠ADB，根据三角形ADC的内角和为180°，等量代换可得证．

解答：

解：

（1）关系：

∠AFC=∠ACB﹣∠DAC，…（2分）

证明：

∵四边形ADEF为正方形，

∴AD=AF，∠FAD=90°，

∵∠BAC=90°，∠FAD=90°，

∴∠BAC+∠CAD=∠FAD+∠CAD，即∠BAD=∠CAF，…（3分）

在△ABD和△ACF中，

，

∴△ABD≌△ACF（SAS），…（4分）

∴∠AFC=∠ADB，

∵∠ACB是△ACD的一个外角，

∴∠ACB=∠ADB+∠DAC，…（5分）

∴∠ADB=∠ACB﹣∠DAC，

∵∠ADB=∠AFC，

∴∠AFC=∠ACB﹣∠DAC；…（6分）

（2）∠AFC、∠ACB、∠DAC满足的关系式为：

∠AFC+∠DAC+∠ACB=180°，…（8分）

证明：

∵四边形ADEF为正方形，

∴∠DAF=90°，AD=AF，

又∠BAC=90°，

∴∠DAF=∠BAC，

∴∠DAF﹣∠BAF=∠BAC﹣∠BAF，即∠DAB=∠FAC，

在△ABD和△ACF中，

，

∴△ABD≌△ACF（SAS），

∴∠ADB=∠AFC，

在△ADC中，∠ADB+∠ACB+∠DAC=180°，

则∠AFC+∠ACB+∠DAC=180°．

点评：

此题考查了正方形的性质，全等三角形的判定与性质，三角形的内角和定理，以及三角形的外角性质，熟练掌握判定及性质是解本题的关键．

8．已知四边形ABCD是正方形，O为正方形对角线的交点，一动点P从B开始，沿射线BC运动，连接DP，作CN⊥DP于点M，且交直线AB于点N，连接OP，ON．（当P在线段BC上时，如图1：

当P在BC的延长线上时，如图2）

（1）请从图1，图2中任选一图证明下面结论：

①BN=CP；②OP=ON，且OP⊥ON；

（2）设AB=4，BP=x，试确定以O、P、B、N为顶点的四边形的面积y与x的函数关系．

考点：

正方形的性质；分段函数；三角形的面积；全等三角形的判定与性质．718351

专题：

代数几何综合题．

分析：

（1）根据正方形的性质得出DC=BC，∠DCB=∠CBN=90°，求出∠CPD=∠DCN=∠CNB，证△DCP≌△CBN，求出CP=BN，证△OBN≌△OCP，推出ON=OP，∠BON=∠COP，求出∠PON=∠COB即可；

（2）同法可证图2时，OP=ON，OP⊥ON，图1中，S四边形OPBN=S△OBN+S△BOP，代入求出即可；图2中，S四边形OBNP=S△POB+S△PBN，代入求出即可．

解答：

（1）证明：

如图1，

∵正方形ABCD，

∴OC=OB，DC=BC，∠DCB=∠CBA=90°，∠OCB=∠OBA=45°，∠DOC=90°，DC∥AB，

∵DP⊥CN，

∴∠CMD=∠DOC=90°，

∴∠BCN+∠CPD=90°，∠PCN+∠DCN=90°，

∴∠CPD=∠CNB，

∵DC∥AB，

∴∠DCN=∠CNB=∠CPD，

∵在△DCP和△CBN中

，

∴△DCP≌△CBN，

∴CP=BN，

∵在△OBN和△OCP中

，

∴△OBN≌△OCP，

∴ON=OP，∠BON=∠COP，

∴∠BON+∠BOP=∠COP+∠BOP，

即∠NOP=∠BOC=90°，

∴ON⊥OP，

即ON=OP，ON⊥OP．

（2）解：

∵AB=4，四边形ABCD是正方形，

∴O到BC边的距离是2，

图1中，S四边形OPBN=S△OBN+S△BOP，

=

×（4﹣x）×2+

×x×2，

=4（0＜x＜4），

图2中，S四边形OBNP=S△POB+S△PBN

=

×x×2+

×（x﹣4）×x

=

x2﹣x（x＞4），

即以O、P、B、N为顶点的四边形的面积y与x的函数关系是：

．

点评：

本题考查了正方形性质，全等三角形的性质和判定，分段函数等知识点的应用，解

（1）小题的关键是能运用性质进行推理，解

（2）的关键是求出符合条件的所有情况，本题具有一定的代表性，是一道比较好的题目，注意：

证明过程类似．

9．如图，四边形ABCD是正方形，点E，K分别在BC，AB上，点G在BA的延长线上，且CE=BK=AG．

（1）求证：

①DE=DG；②DE⊥DG

（2）尺规作图：

以线段DE，DG为边作出正方形DEFG（要求：

只保留作图痕迹，不写作法和证明）；

（3）连接

（2）中的KF，猜想并写出四边形CEFK是怎样的特殊四边形，并证明你的猜想：

（4）当

时，请直接写出

的值．

考点：

正方形的性质；全等三角形的判定与性质；平行四边形的判定；作图—复杂作图．718351

分析：

（1）由已知证明DE、DG所在的三角形全等，再通过等量代换证明DE⊥DG；

（2）根据正方形的性质分别以点G、E为圆心以DG为半径画弧交点F，得到正方形DEFG；

（3）由已知首先证四边形CKGD是平行四边形，然后证明四边形CEFK为平行四边形；

（4）由已知表示出

的值．

解答：

（1）证明：

∵四边形ABCD是正方形，

∴DC=DA，∠DCE=∠DAG=90°．

又∵CE=AG，

∴△DCE≌△DAG，

∴DE=DG，

∠EDC=∠GDA，

又∵∠ADE+∠EDC=90°，

∴∠ADE+∠GDA=90°

∴DE⊥DG．

（2）解：

如图．

（3）解：

四边形CEFK为平行四边形．

证明：

设CK、DE相交于M点

∵四边形ABCD和四边形DEFG都是正方形，

∴AB∥CD，AB=CD，EF=DG，EF∥DG，

∵BK=AG，

∴KG=AB=CD，

∴四边形CKGD是平行四边形，

∴CK=DG=EF，CK∥DG，

∴∠KME=∠GDE=∠DEF=90°，

∴∠KME+∠DEF=180°，

∴CK∥EF，

∴四边形CEFK为平行四边形．

（4）解：

∵

，

∴设CE=x，CB=nx，

∴CD=nx，

∴DE2=CE2+CD2=n2x2+x2=（n2+1）x2，

∵BC2=n2x2，

∴

=

=

．

点评：

此题考查的知识点是正方形的性质、全等三角形的判定和性质、平行四边形的判定及作图，解题的关键是先由正方形的性质通过证三角形全等得出结论，此题较复杂．