系统建模与仿真习题1及答案.docx

系统建模与仿真习题1及答案.docx

《系统建模与仿真习题1及答案.docx》由会员分享，可在线阅读，更多相关《系统建模与仿真习题1及答案.docx（25页珍藏版）》请在冰豆网上搜索。

系统建模与仿真习题1及答案

系统建模与仿真习题一及答案

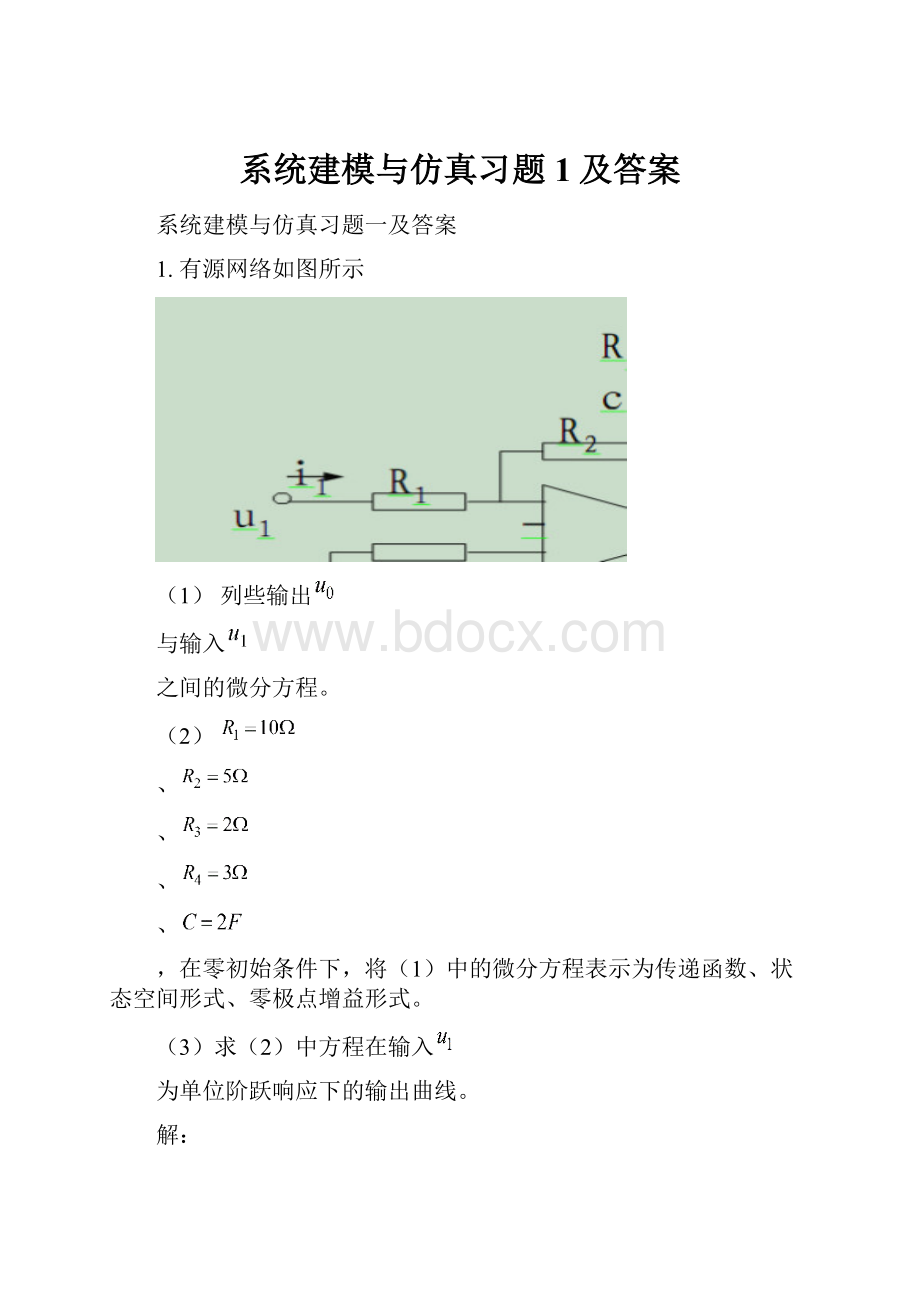
1.有源网络如图所示

（1）列些输出

与输入

之间的微分方程。

（2）

、

、

、

、

，在零初始条件下，将

（1）中的微分方程表示为传递函数、状态空间形式、零极点增益形式。

（3）求

（2）中方程在输入

为单位阶跃响应下的输出曲线。

解：

（1）由运算放大器的基本特点以及电压定理

（3）式代入

（2）式得：

（5）

消去中间变量

有

两边求导整理后得

（2）

代入数据可以得到微分方程为：

程序如下：

clc;clear;

num=[-6.2-0.7];

den=[101];

Gtf=tf（num,den）

Gss=ss（Gtf）

Gzpk=zpk（Gtf）

结果：

Transferfunction:

-6.2s-0.7

------------

10s+1

状态空间形式：

a=

x1

x1-0.1

b=

u1

x10.125

c=

x1

y1-0.064

d=

u1

y1-0.62

Continuous-timemodel.

Zero/pole/gain:

-0.62（s+0.1129）

----------------

（s+0.1）

（3）

由

（2）知系统的传递函数为

-6.2s-0.7

------------

10s+1

系统的输入信号为单位阶跃函数，则其Laplace变换为1/s，这样系统的输出信号的Laplace变换为

Y（s）=

-6.2s-0.7

------------

10s^2+s

编写程序，将其表示为（R,P,Q）形式

clc;clear;

s=tf（'s'）

Gtf=（-6.2*s-0.7）/（10*s^2+s）

[num,den]=tfdata（Gtf,'v'）

[R,P,Q]=residue（num,den）

R=

0.0800

-0.7000

P=

-0.1000

0

Q=

[]

于是得到：

绘制曲线程序：

clc;clear;

t=0:

0.1:

100;

y=0.08*exp（-0.1*t）-0.7;

plot（t,y）

2.已知系统的框图如下：

其中：

G1=1/（s+1），G2=s/（s^2+2），G3=1/s^2，G4=（4*s+2）/（s+1）^2，G5=（s^2+2）/（s^3+14）。

（1）根据梅森公式求总系统传递函数

（2）根据节点、支点、相加点移动方法求总系统传递函数

（3）根据feedback（）函数求总系统传递函数

解：

（1）

前向通道传递函数为

三个回路：

，

，

两个不接触回路：

clc;clear;

s=tf（'s'）;

G1=1/（s+1）;

G2=s/（s^2+2）;

G3=1/s^2;

G4=（4*s+2）/（s+1）^2;

G5=（s^2+2）/（s^3+14）;

G=minreal（3*G3*G2*G1/（1+G4*G2*G1+50*G3+G5*G3*G2*G1+50*G3*G4*G2*G1））

结果：

Transferfunction:

3s^6+6s^5+3s^4+42s^3+84s^2+42s

------------------------------------------------------------------------------------------------------------------------------------------

s^10+3s^9+55s^8+175s^7+300s^6+923s^5+2456s^4+3715s^3+2132s^2+2802s+1400

（2）

，

，

构成反馈回路

50，

构成反馈回路

clc;clear;

s=tf（'s'）;

G1=1/（s+1）;

G2=s/（s^2+2）;

G3=1/s^2;

G4=（4*s+2）/（s+1）^2;

G5=（s^2+2）/（s^3+14）;

G124=G2*G1/（1+G2*G1*G4）;

G350=G3/（1+G3*50）;

G=minreal（3*G350*G124/（1+G350*G124*G5））

结果：

Transferfunction:

3s^6+6s^5+3s^4+42s^3+84s^2+42s

------------------------------------------------------------------------------------------------------------------------------------------

s^10+3s^9+55s^8+175s^7+300s^6+923s^5+2456s^4+3715s^3+2132s^2+2802s+1400

（3）

clc;clear;

s=tf（'s'）;

G1=1/（s+1）;

G2=s/（s^2+2）;

G3=1/s^2;

G4=（4*s+2）/（s+1）^2;

G5=（s^2+2）/（s^3+14）;

G124=feedback（G2*G1,G4）;

G350=feedback（G3,50）;

G=minreal（3*feedback（G350*G124,G5））

结果：

Transferfunction:

3s^6+6s^5+3s^4+42s^3+84s^2+42s

------------------------------------------------------------------------------------------------------------------------------------------

s^10+3s^9+55s^8+175s^7+300s^6+923s^5+2456s^4+3715s^3+2132s^2+2802s+1400

3.已知系统的传递函数模型为：

（1）采用tf（）函数将该传递函数模型输入到MATLAB环境。

（2）采用zpk（）、tf2zp（）函数将上述传递函数模型转化为零极点增益模型。

（3）采用ss（）、tf2ss（）函数将上述传递函数模型转化为状态空间模型。

（4）采用tf（）、ss2tf（）将（3）中变换后的状态空间模型回变为传递函数模型，并与

（1）的结果进行比较。

（5）采用Residue（）函数将上述传递函数模型转化为部分分式模型。

（6）绘制系统的零极点图。

解：

（1）

clc;clear;

num=[1042];

den1=conv（[101],conv（[101],[101]））+[0000025];

den=conv（[1,0],conv（[1,0],conv（[1,0],conv（[1,02],den1））））;

G=tf（num,den）

结果：

s^3+4s+2

-------------------------------------------------------------------

s^11+5s^9+9s^7+2s^6+12s^5+4s^4+12s^3

（2）

clc;clear;

num=[1042];

den1=conv（[101],conv（[101],[101]））+[0000025];

den=conv（[1,0],conv（[1,0],conv（[1,0],conv（[1,02],den1））））;

G=tf（num,den）;

sys=zpk（G）

[z,p,k]=tf2zp（num,den）

结果：

（s+0.4735）（s^2-0.4735s+4.224）

-------------------------------------------------------------------------------------------------------

s^3（s^2+1.544s+1.227）（s^2-1.762s+1.755）（s^2+2）（s^2+0.2176s+2.786）

z=

0.2367+2.0416i

0.2367-2.0416i

-0.4735

p=

0

0

0

0.8810+0.9896i

0.8810-0.9896i

-0.7722+0.7940i

-0.7722-0.7940i

-0.1088+1.6657i

-0.1088-1.6657i

-0.0000+1.4142i

-0.0000-1.4142i

k=

1

（3）

clc;clear;

num=[1042];

den1=conv（[101],conv（[101],[101]））+[0000025];

den=conv（[1,0],conv（[1,0],conv（[1,0],conv（[1,02],den1））））;

G=tf（num,den）;

sys=ss（G）

[A,B,C,D]=tf2ss（num,den）

结果：

a=

x1x2x3x4x5x6x7x8x9x10

x10-1.250-1.125-0.25-0.75-0.25-0.7500

x24000000000

x30200000000

x40010000000

x50001000000

x60000200000

x70000010000

x80000001000

x90000000100

x100000000020

x110000000000.5

x11

x10

x20

x30

x40

x50

x60

x70

x80

x90

x100

x110

b=

u1

x10.5

x20

x30

x40

x50

x60

x70

x80

x90

x100

x110

c=

x1x2x3x4x5x6x7x8x9x10x11

y100000000.12500.250.25

d=

u1

y10

Continuous-timemodel.

A=

0-50-9-2-12-4-12000

10000000000

01000000000

00100000000

00010000000

00001000000

00000100000

00000010000

00000001000

00000000100

00000000010

B=

1

0

0

0

0

0

0

0

0

0

0

C=

00000001042

D=

0

（4）

clc;clear;

num=[1042];

den1=conv（[101],conv（[101],[101]））+[0000025];

den=conv（[1,0],conv（[1,0],conv（[1,0],conv（[1,02],den1））））;

G=tf（num,den）;

sys=ss（G）;

[A,B,C,D]=tf2ss（num,den）;

sys=tf（sys）

[num,den]=ss2tf（A,B,C,D）

结果：

Transferfunction:

s^3-1.11e-016s^2+4s+2

---------------------------------------------------------------------------------------------------------------------------

s^11+4.816e-015s^10+5s^9+2.386e-014s^8+9s^7+2s^6+12s^5+4s^4+12s^3

num=

Columns1through9

00.000000.0000-0.00000.00000.0000-0.00001.0000

Columns10through12

0.00004.00002.0000

den=

Columns1through9

1.0000-0.00005.00000.00009.00002.000012.00004.000012.0000

Columns10through12

000

（5）

clc;clear;

num=[1042];

den1=conv（[101],conv（[101],[101]））+[0000025];

den=conv（[1,0],conv（[1,0],conv（[1,0],conv（[1,02],den1））））;

[R,P,Q]=residue（num,den）

结果：

R=

-0.0246+0.0089i

-0.0246-0.0089i

0.0833+0.0295i

0.0833-0.0295i

0.0274+0.0298i

0.0274-0.0298i

0.0435+0.0581i

0.0435-0.0581i

-0.2593

0.2778

0.1667

P=

-0.1088+1.6657i

-0.1088-1.6657i

-0.0000+1.4142i

-0.0000-1.4142i

0.8810+0.9896i

0.8810-0.9896i

-0.7722+0.7940i

-0.7722-0.7940i

0

0

0

Q=

[]

（6）

clc;clear;

num=[1042];

den1=conv（[101],conv（[101],[101]））+[0000025];

den=conv（[1,0],conv（[1,0],conv（[1,0],conv（[1,02],den1））））;

G=tf（num,den）;

pzmap（G）

结果：

4.考虑二阶系统：

系统的输入为

。

（1）利用部分分式模型方法求输出的解析解

，并绘制其曲线。

（2）利用lsim（G,u,t）函数直接绘制系统的输出曲线，并与

（1）的结果比较。

解：

（1）

先求

的Laplace变换

clc;clear;

symst

f=sin（2*t）;

F=laplace（f）

结果：

F=

2/（s^2+4）

于是：

以下求

的部分分式模型：

clc;clear;

s=tf（'s'）;

G=2/（（s^2+2*s+1）*（s^2+4））;

[num,den]=tfdata（G,'v'）;

[R,P,Q]=residue（num,den）

R=

-0.0800+0.0600i

-0.0800-0.0600i

0.1600

0.4000

P=

0.0000+2.0000i

0.0000-2.0000i

-1.0000

-1.0000

Q=

[]

可以得到解析解为：

绘制曲线：

clc;clear;

t=0:

0.1:

50;

y=（-0.0800+0.0600*i）*exp（2*i*t）+（-0.0800-0.0600*i）*exp（-2*i*t）+0.16*exp（-t）+0.4*t.*exp（-t）;

plot（t,y）

（2）

clc;clear;

t=0:

0.1:

50;

s=tf（'s'）;

G=1/（s^2+2*s+1）;

u=sin（2*t）

lsim（G,u,t）

讨论：

在

（1）中得到解析解为：

这个结果前半部分物理意义不能直接表达出来。

如果采用以下变换：

式中：

，

，则可以得出解析解的更简明的形式。

编写以下通用程序：

文件名为bianhuan.m

function[R,P,Q]=bianhuan（num,den）

[R,P,Q]=residue（num,den）;

fork=1:

length（R）

ifimag（P（k））>eps

a=real（R（k））;b=imag（R（k））;

R（k）=-2*sqrt（a^2+b^2）;R（k+1）=-atan2（a,b）;

elseifabs（imag（P（k）））

R（k）=real（R（k））;

end

end

如果P（k）为实数，则（R（k）,P（k））对和标准的residue（）函数中定义是完全一致的。

如果P（k）为复数，则（R（k）,R（k+1））对返回

和

参数，而P（k）的定义仍与residue（）中的一致。

以下编写程序，调用程序调用bianhuan.m，将解析解：

用正弦以及指数的形式表示。

clc;clear;

s=tf（'s'）;

G=2/（（s^2+2*s+1）*（s^2+4））;

[num,den]=tfdata（G,'v'）;

[R,P,Q]=bianhuan（num,den）

结果：

R=

-0.2000

0.9273

0.1600

0.4000

P=

0.0000+2.0000i

0.0000-2.0000i

-1.0000

-1.0000

Q=

[]

于是解析式可以写为：

5.假设离散系统的传递函数为：

，

将该传递函数模型输入到MATLAB环境；将上述传递函数模型转化为零极点增益模型；将上述传递函数模型转化为状态空间模型；采用Residue（）函数将上述传递函数模型转化为部分分式模型。

解：

clc;clear;

num=[100.568];

den=[1-1.21.19-0.99];

G=tf（num,den,0.1）

[z,p,k]=tf2zp（num,den）;

G=zpk（z,p,k,0.1）

[A,B,C,D]=tf2ss（num,den）;

G=ss（A,B,C,D,0.1）

[R,P,Q]=residue（num,den）

结果：

Transferfunction:

z^2+0.568

-----------------------------

z^3-1.2z^2+1.19z-0.99

Samplingtime:

0.1

Zero/pole/gain:

（z^2+0.568）

--------------------------

（z-1）（z^2-0.2z+0.99）

Samplingtime:

0.1

a=

x1x2x3

x11.2-1.190.99

x2100

x3010

b=

u1

x11

x20

x30

c=

x1x2x3

y1100.568

d=

u1

y10

Samplingtime:

0.1

Discrete-timemodel.

R=

0.8760

0.0620-0.1574i

0.0620+0.1574i

P=

1.0000

0.1000+0.9899i

0.1000-0.9899i

Q=

[]