平行四边形证明练习题.docx

平行四边形证明练习题.docx

《平行四边形证明练习题.docx》由会员分享，可在线阅读，更多相关《平行四边形证明练习题.docx（24页珍藏版）》请在冰豆网上搜索。

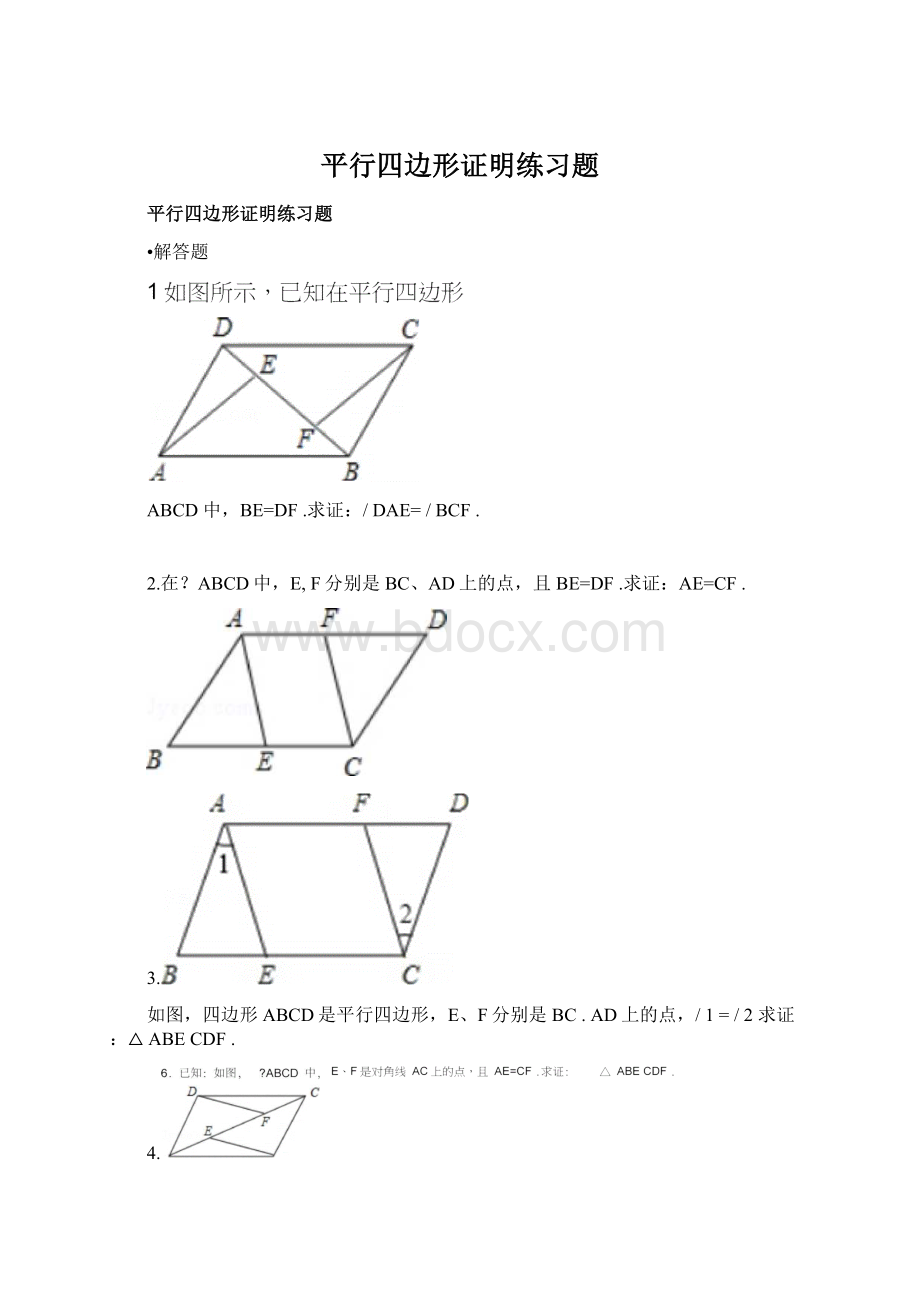
平行四边形证明练习题

平行四边形证明练习题

•解答题

ABCD中，BE=DF.求证：

/DAE=/BCF.

2.在？

ABCD中，E,F分别是BC、AD上的点，且BE=DF.求证：

AE=CF.

3.

如图，四边形ABCD是平行四边形，E、F分别是BC.AD上的点，/1=/2求证：

△ABECDF.

4.

7.如图，已知在？

ABCD中，过AC中点的直线交CD,AB于点E,F.求证：

DE=BF.

ABCD是平行

10.如图，四边形ABCD中，AD=BC，AE丄BD,CF丄BD，垂足为E、F,AE=CF，求证：

四边形四边形.

11.如图，在厶ABC中，AD是中线，点E是AD的中点，过A点作BC的平行线交CE的延长线于点

12.如图，在等腰梯形ABCD中，AD//BC,AB=DC,DE//AB,AD+DC=BC求证：

（1）DE=DC;

13.已知：

如图，E、F是平行四边形ABCD的对角线AC上的两点，AE=CF.求证：

（1）△ADFCBE;

（2）连接DE、BF，试判断四边形DEBF的形状，并说明理由.

14.如图，平行四边形ABCD中，点E、F、G、H分别在AB、BC、CD、AD边上且AE=CG,AH=CF.求证：

四边形EFGH是平行四边形.

15.如图，在平行四边形ABCD中，E、F是对角线AC上的点，且AE=CF.

（1）猜想探究：

BE与DF之间的关系：

__

（2）

请证明你的猜想.

18.如图，BD是？

ABCD的对角线，/ABD的平分线BE交AD于点E,/CDB的平分线DF交BC于点F.求证:

四边形DEBF为平行四边形.

19.如图，在?

ABCD中，对角线AC与BD交于点0,已知点E、F分别为AO、OC的中点，证明：

四边形BFDE是平行四边形.

20.如图所示，A,E,F,C在一条直线上，AE=CF，过E,F分别作DE丄AC,BF丄AC,若AB=CD，可以得到BD平分EF，为什么？

说明理由.

21.如图，△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点.求证：

EF=DG且EF//DG.

22.已知如图所示，?

ABCD的对角线AC、BD交于O,GH过点O,分别交AD、BC于G、H,E、F在AC上且

平行四边形证明练习题

参考答案与试题解析

一.解答题（共22小题）

1如图所示，已知在平行四边形ABCD中，BE=DF.求证：

/DAE=/BCF.

考点：

平行四边形的性质；平行线的性质；全等三角形的判定与性质.

分析：

根据平行四边形性质求出AD//BC,且AD=BC，推出/ADE=/CBF，求出DE=BF，证△ADECBF,推出/DAE=/BCF即可.

解答：

证明：

•••四边形ABCD为平行四边形，

•••AD//BC，且AD=BC,

•••/ADE=/CBF

又•••BE=DF,

•BF=DE,

•••在△ADE和△CBF中

rAD=CB

-ZADE^ZCBF,

二BF

•△ADE◎△CBF,

•••/DAE=/BCF.

点评：

本题考查了平行四边形性质，平行线性质，全等三角形的性质和判定的应用，关键是求出证出△ADE和

△CBF全等的三个条件，主要考查学生的推理能力.

2.

在？

ABCD中，E,F分别是BC、AD上的点，且BE=DF.求证：

AE=CF.

考点：

平行四边形的性质；全等三角形的判定与性质.

分析：

根据平行四边形的性质得出AB=CD，/B=/D，根据SAS证出△ABE◎△CDF即可推出答案.

解答：

证明：

•••四边形ABCD是平行四边形，

•AB=CD，/B=/D,

•/BE=DF,

•△ABE◎△CDF,

•AE=CF.

点评：

本题主要考查对平行四边形的性质，全等三角形的性质和判定等知识点的理解和掌握，能根据性质证出△ABECDF是证此题的关键.

3.如图，四边形ABCD是平行四边形，E、F分别是BC.AD上的点，/1=/2

求证：

△ABE◎△CDF.

考点：

平行四边形的性质；全等三角形的判定.

分析：

禾U用平行四边形的性质和题目提供的相等的角可以为证明三角形全等提供足够的条件.解答：

证明：

•••四边形ABCD是平行四边形，

•••/B=/D,AB=CD,

•在：

△ABE与厶CDF中，

-AB二CD

lzb=zd

•••△ABECDF（ASA）

点评：

本题考查了平行四边形的性质及全等三角形的判定，根据平行四边形找到证明全等三角形足够的条件是解决本题的关键.

4.如图，已知：

平行四边形ABCD中，E是CD边的中点，连接BE并延长与AD的延长线相交于F点.求证:

BC=DF.

考点：

平行四边形的性质；全等三角形的判定与性质.分析：

由四边形ABCD是平行四边形，可得AD//BC,根据平行线的性质即可求得/EBC=/F,ZC=ZEDF，又

由E是CD边的中点，根据AAS即可求得△EBCEFD，则问题得证.

解答：

证明：

•••四边形ABCD是平行四边形,

•••AD//BC,

•••/EBC=/F,ZC=ZEDF,又•••EC=ED,

•••△EBC◎△EFD（AAS）,

•BC=DF.

点评：

此题考查了平行四边形的性质以及全等三角形的判定与性质•此题难度不大，解题的关键是要注意数形结合思想的应用.

5.（2013?

莒南县二模）如图，在？

ABCD中，AC交BD于点O,点E、点F分别是OA、OC的中点，请判断线段

考点：

平行四边形的性质；全等三角形的判定与性质.

分析：

根据平行四边形的性质对角线互相平分得出OA=OC,OB=OD，利用中点的意义得出OE=OF，从而利用平

行四边形的判定定理对角线互相平分的四边形是平行四边形”判定BFDE是平行四边形，从而得出BE=DF,

BE//DF.

解答：

解：

由题意得：

BE=DF,BE//DF•理由如下：

连接DE、BF•

•••ABCD是平行四边形，

•••OA=OC,OB=OD,

•••E,F分别是OA,OC的中点，

•OE=OF,

•BFDE是平行四边形，

•

BE=DF,BE//DF•

6.

已知：

如图，？

ABCD中，E、F是对角线AC上的点，且AE=CF•求证：

△ABECDF.

考点：

平行四边形的性质；平行线的性质；全等三角形的判定.

分析：

根据平行四边形的性质得出AB//DC,AB=CD，根据平行线的性质推出/BAC=/DCF，根据SAS证出即

可.

解答：

证明：

•••四边形ABCD是平行四边形,

•AB//DC,AB=CD,

•/BAC=/DCF,

•/AE=CF,

•△ABECDF.

点评：

本题主要考查对平行四边形的性质，全等三角形的判定，平行线的性质等知识点的理解和掌握，能推出证

△ABE◎△CDF的三个条件是解此题的关键.

7.

DE=BF.

如图，已知在？

ABCD中，过AC中点的直线交CD,AB于点E,F.求证:

考点：

平行四边形的性质；平行线的性质；全等三角形的判定与性质.

解答：

证明：

•••四边形ABCD是平行四边形，

•••DC=AB,DC//AB,

•••/ECA=/BAC，/CEO=/AFO,

•/OA=OC,

•△AOF◎△COE,

•CE=AF,•/DC=AB,

•DE=BF.

点评：

本题主要考查对平行四边形的性质，平行线的性质，全等三角形的性质和判定等知识点的理解和掌握，解此题的关键是根据平行四边形的性质证出△AOF和厶COE全等.

&如图，在等腰梯形ABCD中，AD//BC,AB=CD=AE.四边形AECD是平行四边形吗？

为什么？

AD

考点：

等腰梯形的性质；平行线的判定与性质；等腰三角形的性质；平行四边形的判定.

分析：

根据等腰三角形性质求出/B=/C,根据等腰三角形性质推出/AEC=/B=/C,推出AE//CD，根据平行四边形的判定推出即可.

解答：

解：

是平行四边形，

理由：

•••四边形ABCD是等腰梯形，AD//BC,

•AB=DC，/B=/C,

•/AB=AE,

•/AEB=/B,

•/AEB=/C,

•AE//DC,

又•••AD//BC,

•四边形AECD是平行四边形.

点评：

本题考查了等腰三角形的性质，等腰梯形的性质，平行线的性质和判定，平行四边形的判定等知识点的应用，关键是根据题意推出AE//CD，培养了学生分析问题和解决问题的能力，题目较好，综合性比较强.

9.如图，E、F是平行四边形ABCD的对角线AC上的两点，AE=CF.求证：

DE=BF.

j=D

考点：

平行四边形的性质；全等三角形的判定与性质；平行四边形的判定.

•/AE=CF,

•••OE=OF,

•••四边形BEDF是平行四边形,

点评：

本题考查了平行四边形的性质和判定等应用，关键是能熟练地运用平行四边形的性质和判定进行推理，此题的证明方法二是证△AED◎△CFB，推出DE=BF.

10.如图，四边形ABCD中，AD=BC,AE丄BD,CF丄BD，垂足为E、F,AE=CF，求证：

四边形ABCD是平行四边形.

考点：

平行四边形的判定；平行线的性质；全等三角形的判定与性质.

分析：

求出/AED=/CFB=90°根据HL证Rt△AED也Rt△CFB，推出/ADE=/CBD，得到AD//BC,根据平行四边形的判定判断即可.

解答：

证明：

TAE丄BD,CF丄BD,•••/AED=/CFB=90°在Rt△AED和Rt△CFB中/AE=CF

\ad=bc，

•Rt△AED也Rt△CFB（HL）,•••/ADE=/CBD,

•AD//BC,

•/AD=BC,

•四边形ABCD是平行四边形.

点评：

本题考查了平行四边形的判定，平行线的性质，全等三角形的性质和判定等知识点的应用，关键是推出

AD//BC,主要考查学生运用性质进行推理的能力.

11.如图，在厶ABC中，AD是中线，点E是AD的中点，过A点作BC的平行线交CE的延长线于点F,连接BF.

考点：

平行四边形的判定；全等三角形的判定与性质.

专题：

证明题.

分析：

求出AE=DE，/AFE=/DCE，证△AEF◎△CED，推出AF=DC，得出AF//BD,AF=BD，根据平行四边形的判定推出即可.

解答：

证明：

•••E为AD中点，

•••AE=DE,

•/AF//BC,

•••/AFE=/DCE,

在厶AEF和厶CED中

rZAFE=ZDCE

lAE=DE

•△AEF◎△CED（AAS）,

•AF=DC,

•/AD是厶ABC的中线，

•BD=DC,

•AF=BD,

即AF//B