初一下册奥数1323讲.docx

初一下册奥数1323讲.docx

《初一下册奥数1323讲.docx》由会员分享，可在线阅读，更多相关《初一下册奥数1323讲.docx（72页珍藏版）》请在冰豆网上搜索。

初一下册奥数1323讲

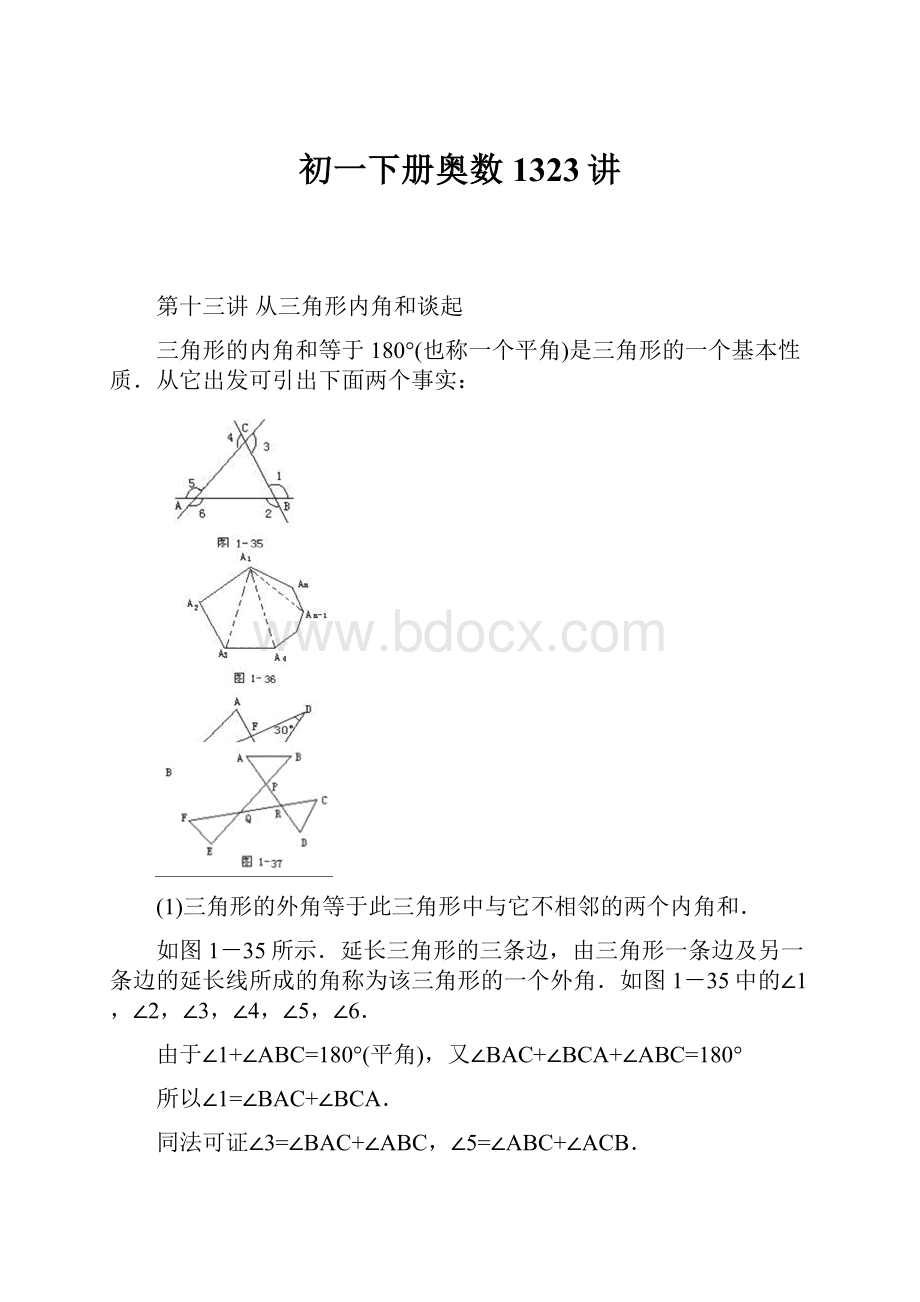
第十三讲从三角形内角和谈起

三角形的内角和等于180°（也称一个平角）是三角形的一个基本性质．从它出发可引出下面两个事实：

（1）三角形的外角等于此三角形中与它不相邻的两个内角和．

如图1－35所示．延长三角形的三条边，由三角形一条边及另一条边的延长线所成的角称为该三角形的一个外角．如图1－35中的∠1，∠2，∠3，∠4，∠5，∠6．

由于∠1+∠ABC=180°（平角），又∠BAC+∠BCA+∠ABC=180°

所以∠1=∠BAC+∠BCA．

同法可证∠3=∠BAC+∠ABC，∠5=∠ABC+∠ACB．

（2）n边形的内角和等于（n-2）×180°

如图1－36所示．以n边形A1A2…An的某一个顶点（如A1）为共同顶点，将这个n边形“分割成”n-2个三角形△A1A2A3，△A1A3A4，…，△A1An-1An．由于每一个三角形的内角和等于180°，所以，这n-2个三角形的内角和（即n边形的内角和）为（n-2）×180°（详证见后面例6）．

三角形内角和等于180°这个事实有着广泛的应用．

例1如图1－37所示．平面上六个点A，B，C，D，E，F构成一个封闭折线图形．求：

∠A+∠B+∠C+∠D+∠E+∠F==360°．

分析所求的六个角分布在三个三角形中，但需减去顶点位于P，Q，R处的三个内角，由图形结构不难看出，这三个内角可以集中到△PQR中．

解在△PAB，△RCD，△QEF中，

∠A+∠B+∠APB=180°①

∠C+∠D+∠CRD=180°②

∠E+∠F+∠EQF=180°③

又在△PQR中,∠QPR+∠PRQ+∠PQR=180°④

又∠APB=∠QPR，∠CRD=∠PRQ，∠EQF=∠PQR（对顶角相等）．

①+②+③-④得∠A+∠B+∠C+∠D+∠E+∠F==360°

说明依据图形的特点，利用几何图形的性质将分散的角集中到某些三角形之中，是利用三角形内角和性质的前提．

例2求如图1－38所示图形中∠A+∠B+∠C+∠D+∠E的大小．

分析如果我们注意力放在三角形内角和上，那么∠ABE=∠ABO+∠OBE，∠AEB=∠AED+∠OEB．而∠ABE，∠AEB属于△ABE，∠OBE，∠OEB属于△OBE，再注意到△OBE及△ODC中，因∠BOE=∠COD（对顶角），因而，∠D+∠C=∠OBE+∠OEB．从而，可求出题中五角和．

解法1连接BE．在△COD中，∠C+∠D+∠COD=180°①

在△ABE中，∠A+∠ABE+∠AEB=180°②

①+②得（∠A+∠C+∠D）+∠COD+∠ABE+∠AEB=360°③

又∠ABE=∠ABO（即为∠B）+∠OBE，∠AEB=∠AEO（即为∠E）+∠OEB．

故③式可化为（∠A+∠B+∠C+∠D+∠E）+（∠COD+∠OBE+∠OEB）=360°④

由于∠COD=∠BOE（对顶角相等），

在△BOE中∠COD+∠OBE+∠OEB=∠BOE+∠OBE+∠OEB＝180°

由④得∠A+∠B+∠C+∠D+∠E=180°

解法2如果我们注意到三角形外角的性质，结合图形（图1－39）会发现

在△OCD中有∠1=∠C+∠D，△APE中∠2=∠A+∠E，在△BOP中∠1+∠2+∠B=180°

从而有∠A+∠B+∠C+∠D+∠E=180°

说明本例解法2比解法1简洁，因为我们应用了关于三角形外角的性质．

例3如图1－40所示．在△ABC中，∠B的平分线与∠C的外角平分线交于D，且∠D=30°,求∠A的度数．

分析D位于△BCD中，A位于△ABC中，它们位于两个不同的三角形之中，欲利用三角形内角和定理解决问题，就必须寻求两个三角形中内角之间的关系，角平分线的条件为我们提供了信息，事实上

以及∠DCB=∠ACB+∠ACD（它是∠C外角的一半）.

解由已知，∠D=30°,在△BCD中，∠CBD+∠BCD=180°-30°=150°①

因为BD是∠ABC的平分线，所以

②

又因为CD是∠ACE的平分线，所以

从而

③

由①，②，③得

又因∠ABC+∠ACB+∠A=180°,所以∠A=60°

说明解决本题的关键在于两条角平分线架起了△ABC与△BCD之间的桥梁，完成了从已知向未知的过渡．细心审题，发现已知与所求之间的联系，常是解题的重要前提．

例4如图1-41所示．∠A=10°,∠ABC=90°,∠ACB=∠DCE，∠ADC=∠EDF，∠CED=∠FEG．求∠F的度数．

分析如果我们能注意到所给的一系列等角条件正反映了内角与外角的关系，问题就不难解决．例如在∠ACB=∠DCE中，∠ACB是△ABC的一个内角，∠DCE是△ACD的外角．∠ADC=∠EDF及∠CED=∠FEG两个等式两边的角也是类似情况，这就为我们利用外角定理解题创造了机会．

解在△ABC中，∠A=10°,∠ABC=90°,所以∠ACB＝80°,因为∠DCE=∠ACB=80°

在△ACD中，∠DCE是它的一个外角，所以∠DCE=∠A+∠ADC，即80°=10°+∠ADC，

所以∠ADC=70°,∠EDF=∠ADC=70°

在△ADE中，∠EDF是它的一个外角，所以∠EDF=∠A+∠AED，即70°=10°+∠AED，

所以∠AED=60°,∠FEG=∠AED=60°

在△AEF中，∠FEG是它的一个外角，所以∠FEG=∠A+∠F，

所以∠F=∠FEG-∠A=60°-10°=50°

例5如图1－42所示．△ABC的边BA延长线与外角∠ACE的平分线交于D．求证：

∠BAC＞∠B．

分析三角形的外角定理的意义中已暗含着“三角形的外角大于三角形中与此外角不相邻的内角”的意义．证明有关三角形角的不等问题可从此下手．

证BAC是△ACD的一个外角，因为∠BAC=∠1+∠D，

所以2∠BAC=2∠1+2∠D=∠ACE+2∠D＞∠ACE①（因为CD是∠ACE的平分线．）

又∠ACE是△ABC的一个外角，所以∠ACE=∠B+∠BAC．②

由①,②得2∠BAC＞∠B+∠BAC，所以∠BAC＞∠B．

由于多边形可以分割为若干个三角形，因而多边形的内角和可以转化为三角形内角和来计算．下面我们来求n（n≥3的自然数）边形的内角和．

例6n边形的内角和等于（n-2）×180°。

分析我们不妨先从具体情况入手．

当n=4时，如图1－43所示．四边形ABCD用一条对角线可以分割成两个三角形，因此四边形ABCD的内角和=三角形ABC的内角和+三角形ACD的内角和=2×180°=360°。

当n=5时，如图1－44所示．五边形ABCDE用两条对角线可以分割为三个三角形．类似于n=4的情况，可证明：

五边形ABCDE的内角和=3×180°=540°。

由这两个具体实例，我们可以找到n边形的内角和的证明方法．

证在n边形A1A2A3…An中，以A1为一个端点，连接对角线A1A3，A1A4，…，A1An-1，共有（n-1）-3+1=n-3条对角线，将这个n边形分割成n-2个三角形．显然，这n-2个三角形的内角“合并”起来恰是这个n边形的n个内角，如图1-45所示．

所以n边形的内角和=（n-2）×180°

说明

（1）从具体的简单的问题入手常能找到解决复杂问题的思路．如本题从n=4，5入手，找到将多边形分割为三角形的方法（这是一个本质的方法），从而可以推广到n为任意自然数的范围中去．

（2）各条边都相等，各个内角都相等的多边形称为正多边形．由本例自然可以推出正n边形每一个内角的大小．

设正n边形的一个内角大小为a，则n边形的内角和=na=（n-2）×180°

所以

例如正五边形的内角的度数为

正十边形的内角度数为

练习十三

1．如图1-46所示．求∠A+∠B+∠C+∠D+∠E的大小．

2．如图1-47所示．求∠A+∠B+∠C+∠D+∠E的大小．

3．如图1-48所示．求∠A+∠B+∠C+∠D+∠E的大小．

4．如图1-49所示．求∠A+∠B+∠C+∠D+∠E的大小．．

5．若多边形内角和分别为下列度数时，试分别求出多边形的边数：

（1）1260°

（2）2160°

6．证明：

n边形的外角和等于360°

第十四讲面积问题

我们已经学过的面积公式有：

（1）

（其中h表示a边上的高）

（2）S平行四边形=ah（其中h表示a边上的高）

（3）

（其中a,b表示梯形中两条平行边的长，h表示平行边之间的距离）

由于多边形可以分割为若干个三角形，多边形的面积等于各三角形面积和，因此，三角形的面积是面积问题的基础．

等积变形是面积问题中富于思考性的有趣问题，它是数学课外活动的重要内容，这一讲中我们将花较多的篇幅来研究多边形的等积变形．

等积变形是指保持面积不变的多边形的变形．

三角形的等积变形是多边形等积变形的基础，关于三角形的等积变形有以下几个主要事实：

（1）等底等高的两个三角形面积相等．

（2）两个三角形面积之比，等于它们的底高乘积之比．

（3）两个等底三角形面积之比，等于它们的高之比．

（4）两个等高三角形面积之比等于它们的底之比．

例1已知△ABC中三边长分别为a，b，c，对应边上的高分别为ha=4，hb=5，hc=3．求a∶b∶c．

解设△ABC的面积为S，则有

所以

说明同一个三角形依面积公式可以有三种不同的表示法，由此获得三边之比．

例2如图1－51，平行四边形ABCD的面积为64平方厘米（cm2），E，F分别为AB，AD的中点，求△CEF的面积．

分析由于△CEF的底与高难以从平行四边行的面积中求出，因此，应设法将四边形分割为三角形，利用面积比与底（高）比来解决．

解连接AC．E为AB中点，所以

（平方厘米）

同理可得S△CDF=16（平方厘米）

连接DE，DB，F为AD中点，所以

（平方厘米）

从而S△CEF=S□ABCD-S△AEF-S△BCE-S△CDF=64-16-16-8=24（平方厘米）．

说明

（1）E，F是所在边的中点启发我们添加辅助线BD，DE．

（2）平行四边形的对角线将平行四边形分成两个三角形的面积相等是由平行四边形对边相等及平行线间的距离处处相等，从而这两个三角形的底、高相等获知的．

例3如图1-52所示，已知△ABC的面积为1,且

求△DEF的面积。

分析直接求△DEF面积有困难，观察图形，发现△DEF与△DCF有共同的顶点D，其底边在同一条直线上，因而，高相同．所以

于是，求△DEF的面积就转化为求△DCF的面积．用同样的办法可将△DCF的面积转化为△ADC的面积，进而转化为△ABC的面积．

解因为

所以EF＝2CE,△DEF与△DCF有共同的项点D,且底边EF，CF在同一条直线上，所以

，即EF∶CF=2∶3，

同理，△DCF与△DCA有共同的顶点C，且底边DF，DA在同一条直线上，由已知DF∶DA=2∶3，

所以

所以

例4面积方法证明：

三角形两边中点连线平行于第三边．

分析与解如图1－53所示．设E，F分别是AB，AC的中点，可求得△EBC与△FBC的面积相等（均为△ABC面积的一半）．由于这两个三角形同底BC，因而这两个三角形的顶点E，F在一条与底边BC平行的直线上，所以EF∥BC．

说明

（1）从证题过程看出，条件“E，F是所在边的中点”可以推广为

等，事实上

从而S△CBE=S△BCF．

这两个三角形同底BC，因此，它们的顶点E，F的连线与底边平行．

（2）同样用面积的方法可以证明如下事实：

三角形ABC中，若EF∥BC且AE∶EB=m，则AF∶FC=m（请同学们自己证明）．

例5如图1－54．在△ABC中，E是AB的中点，D是AC上的一点，且AD∶DC=2∶3，BD与CE交于F，S△ABC=40，求S四边形AEFD．

分析四边形AEFD可分割为△AED与△DEF．从E是AB中点及D分AC为2∶3的条件看，△AED的面积不难推知，关键是如何推求△DEF的面积．为此，需通过添加辅助线的办法，寻求△DEF的面积与已知面积的关系．

解取AD的中点G，并连接EG，在△ABD中，E是AB的中点，由例3知EG∥BD．又CD∶DG=3∶1，从而，在△CEG中，

CF∶FE=CD∶DG=3∶1（例3说明

（2）），

所以S△DFC∶S△DFE=3∶1．

设S△DEF=x，则S△DFC=3x，S△DEC=4x．由于AD∶DC=2∶3，

所以S△EAD∶S△ECD=2∶3，

于时

又因E是AB的中点，所以

，

所以x=3，即S△DEF=3,所以S△ADE=8，所以S四边形AEFD=S△ADE+S+=8+3=11．

说明在三角形中，利用平行线实行比的转移，再利用等积变形，得到相应的面积的比，从而将欲求的△DEF的面积与已知的△ABC的面积“挂上了钩”．这里取AD的中点G，得到BD的平行线EG是关键．

例6如图1-55所示．E，F分别是平行四边形ABCD的边AD，AB上的点，且BE=DF，BE与DF交于O．求证：

C点到BE的距离等于它到DF的距离．

分析过C作CG⊥BE于G，CH⊥FD于H，则CG，CH分别是C到BE，DF的距离，问题就是要证明CG=CH．结合已知，BE=DF，可以断言，△BCE的面积等于△CDF的面积．由于这两个三角形的面积都等于平行四边形ABCD面积的一半，因此它们等积，问题获解．

解连接CF，CE．因为

S△BCE=

所以S△BCE=S△CDF．

因为BE=DF，所以CG=CH（CG，CH分别表示BE，DF上的高），

即C点到BE和DF的距离相等．

说明

（1）△BCE与△CDF是两个形状及位置完全不同的三角形，它们面积相等正是通过等积变形——都等于同一平行四边形的面积之半．

（2）通过等积变形可以证明线段的相等．

练习十四

1．如图1－56所示．在△ABC中，EF∥BC，且AE∶EB=m，求证：

AF∶FC=m．

2．如图1－57所示．在梯形ABCD中，AB∥CD．若△DCE的面积是△DCB面积的

，问△DCE的面积是△ABD面积的的几分之几？

3．如图1－58所示．已知P为△ABC内一点，AP，BP，CP分别与对边交于D，E，F，把△ABC分成六个小三角形，其中四个小三角形的面积已在图中给出．求△ABC的面积．

4．如图1－59所示．P为△ABC内任意一点，三边a，b，c的高分别为ha，hb，hc，且P到a，b，c的距离分别为ta，tb，tc．

求证：

5．如图1－60所示．在梯形ABCD中，两腰BA，CD的延长线相交于O，OE∥DB，OF∥AC且分别交直线BC于E，F．求证：

BE=CF．

6．如图1－61所示．P是△ABC的AC边的中点，PQ⊥AC交AB延长线于Q，BR⊥AC于R．求证：

第十五讲奇数与偶数

通常我们所说的“单数”、“双数”，也就是奇数和偶数，即±1，±3，±5，…是奇数，0，±2，±4，±6，…是偶数．

用整除的术语来说就是：

能被2整除的整数是偶数，不能被2整除的整数是奇数．通常奇数可以表示为2k+1（或2k-1）的形式，其中k为整数，偶数可以表示为2k的形式，其中k是整数．

奇数和偶数有以下基本性质：

性质1奇数≠偶数．

性质2奇数±奇数=偶数，偶数±偶数=偶数，奇数±偶数=奇数．

性质3奇数×奇数=奇数，偶数×偶数=偶数，奇数×偶数=偶数．

性质4奇数个奇数之和是奇数；偶数个奇数之和是偶数；任意有限个偶数之和为偶数．

性质5若干个奇数的乘积是奇数，偶数与整数的乘积是偶数．

性质6如果若干个整数的乘积是奇数，那么其中每一个因子都是奇数；如果若干个整数的乘积是偶数，那么其中至少有一个因子是偶数．

性质7如果两个整数的和（或差）是偶数，那么这两个整数的奇偶性相同；如果两个整数的和（或差）是奇数，那么这两个整数一定是一奇一偶．

性质8两个整数的和与差的奇偶性相同．

性质9奇数的平方除以8余1，偶数的平方是4的倍数.

性质1至性质6的证明是很容易的，下面我们给出性质7至性质9的证明．

性质7的证明设两个整数的和是偶数，如果这两个整数为一奇一偶，那么由性质2知，它们的和为奇数，因此它们同为奇数或同为偶数．

同理两个整数的和（或差）是奇数时，这两个数一定是一奇一偶．

性质8的证明设两个整数为X，y．因为（x+y）+（x-y）=2x为偶数，由性质7便知，x+y与x-y同奇偶．

性质9的证明若x是奇数，设x=2k+1，其中k为整数，于是x2=（2k+1）2=4k2+4k+1=4k（k+1）+1．

因为k与k+1是两个连续的整数，它们必定一奇一偶，从而它们的乘积是偶数．于是，x2除以8余1．

若y是偶数，设y=2t，其中t为整数，于是y2=（2t）2=4t2

所以，y2是4的倍数．

例1在1，2，3，…，1998中的每一个数的前面，任意添上一个“+”或“-”，那么最后运算的结果是奇数还是偶数？

解由性质8知，这最后运算所得的奇偶性同1+2+3+…+1998=999×1999的奇偶性是相同的，即为奇数．

例2设1，2，3，…，9的任一排列为a1，a2，…，a9.求证：

（a1-1）（a2-2）…（a9-9）是一个偶数．

证法1因为（a1-1）+（a2-2）+（a3-3）+…+（a9-9）＝（a1+a2+……+a9）-（1+2+…+9）=0是偶数，

所以，（a1-1），（a2-2），…，（a9-9）这9个数中必定有一个是偶数（否则，便得奇数个（9个）奇数的和为偶数，与性质4矛盾），从而由性质5知

（a1-1）（a2-2）…（a9-9）是偶数．

证法2由于1，2，…，9中只有4个偶数，所以a1，a3，a5，a7，a9中至少有一个是奇数，于是，a1-1，a3-3，a5-5，a7-7，a9-9至少有一个是偶数，从而（a1-1）（a2-2）…（a9-9）是偶数．

例3有n个数x1，x2，…，xn，它们中的每一个数或者为1，或者为-1．

如果x1x2+x2x3+…+xn-1xn+xnx1=0，求证：

n是4的倍数．

证我们先证明n=2k为偶数，再证k也是偶数．

由于x1，x2，…，xn的绝对值都是1，所以，x1x2，x2x3，…，xnx1的绝对值也都是1，即它们或者为+1，或者为-1．设其中有k个-1，由于总和为0，故+1也有k个，从而n=2k．

下面我们来考虑（x1x2）（x2x3）…（xnx1）．一方面，有（x1x2）（x2x3）…（xnx1）＝（-1）k，

另一方面，有（x1x2）（x2x3）…（xnx1）=（x1x2…xn）2=1．

所以（-1）k=1，故k是偶数，从而n是4的倍数．

例4设a，b是自然数，且满足关系式（11111+a）（11111-b）=123456789．求证：

a-b是4的倍数．

证由已知条件可得11111+a与11111-b均为奇数，所以a，b均为偶数．

又由已知条件11111（a-b）=ab+2468，①

ab是4的倍数，2468=4×617也是4的倍数，所以11111×（a-b）是4的倍数，故a-b是4的倍数.

例5某次数学竞赛，共有40道选择题，规定答对一题得5分，不答得1分，答错倒扣1分．证明：

不论有多少人参赛，全体学生的得分总和一定是偶数．

证我们证明每一个学生的得分都是偶数．

设某个学生答对了a道题，答错了b道题，那么还有40-a-b道题没有答．于是此人的得分是

5a+（40-a-b）-b=4a-2b+40，这是一个偶数．

所以，不论有多少人参赛，全体学生的得分总和一定是偶数．

例6证明15块4×1的矩形骨牌和1块2×2的正方形骨牌不能盖住8×8的正方形.

证将8×8正方形的小方格用黑、白色涂色（如图1－62）．每一块4×1骨牌不论怎么铺设都恰好盖住两个白格，

因此15块4×1的骨牌能盖住偶数个白格．一块2×2的骨牌只能盖住一个白格或三个白格，总之能盖住奇数个白格．于是15块4×1骨牌和一块2×2骨牌在图上盖住的白格是奇数个．事实上图上的白格数恰为偶数个，故不能盖住8×8的正方形．

练习十五

1．设有101个自然数，记为a1，a2，…，a101．已知a1+2a2+3a3+„+100a100+101a101=s是偶数，求证：

a1+a3+a5+…+a99+a101是偶数．

2．设x1，x2，…，x1998都是+1或者-1．求证：

x1+2x2+3x3+„+1998x1998≠0．

3．设x1，x2，…，xn（n＞4）为1或-1，并且x1x2x3x4+x2x3x4x5+…+xnx1x2x3=0．求证：

n是4的倍数．

4．

（1）任意重排某一自然数的所有数字，求证：

所得数与原数之和不等于99…9（共n个9，n是奇数）；

（2）重排某一数的所有数字，并把所得数与原数相加，求证：

如果这个和等于1010，那么原数能被10整除．

5．

（1）有n个整数，其和为零，其积为n．求证：

n是4的倍数；

（2）设n是4的倍数，求证：

可以找到n个整数，其积为n，其和为零．

6．7个杯子杯口朝下放在桌子上，每次翻转4个杯子（杯口朝下的翻为杯口朝上，杯口朝上的翻为杯口朝下），问经过若干次这样的翻动，是否能把全部杯子翻成杯口朝上？

7．能否把1，1，2，2，3，3，4，4，5，5这10个数排成一行，使得两个1中间夹着1个数，两个2之间夹着2个数，…，两个5之间夹着5个数？

第十六讲质数与合数

我们知道，每一个自然数都有正因数（因数又称约数）．例如，1有一个正因数；2，3，5都有两个正因数，即1和其本身；4有三个正因数：

1，2，4；12有六个正因数：

1，2，3，4，6，12．由此可见，自然数的正因数，有的多，有的少．除了1以外，每个自然数都至少有两个正因数．我们把只有1和其本身两个正因数的自然数称为质数（又称素数），把正因数多于两个的自然数称为合数．这样，就把全体自然数分成三类：

1、质数和合数．

2是最小的质数，也是唯一的一个既是偶数又是质数的数．也就是说，除了2以外，质数都是奇数，小于100的质数有如下25个：

2，3，5，7，11，13，17，19，23，29，31，37，41，43，47，53，59，61，67，71，73，79，83，89，97．

质数具有许多重要的性质：

性质1一个大于1的正整数n，它的大于1的最小因数一定是质数．

性质2如果n是合数，那么n的最小质因数a一定满足a2≤n．

性质3质数有无穷多个（这个性质将在例6中证明）．

性质4（算术基本定理）每一个大于1的自然数n，必能写成以下形式：

n=p1a1p2a2…prar，这里的P1，P2，…，Pr是质数，a1，a2，…，ar是自然数．如果不考虑p1，P2，…，Pr的次序，那么这种形式是唯一的．

关于质数和合数的问题很多，著名的哥德巴赫猜想就是其中之一．哥德巴赫猜想是：

每一个大于2的偶数都能写成两个质数的和．这是至今还没有解决的难题，我国数学家陈景润在这个问题上做了到目前为止最好的结果，他证明了任何大于2的偶数都是两个质数的和或一个质数与一个合数的和，而这个合数是两个质数的积（这就是通常所说的1+2）．下面我们举些例子．

例1设p，q，r都是质数，并且p+q=r，p＜q．求p．

解由于r=p+q，所以r不是最小的质数，从而r是奇数，所以p，q为一奇一偶．因为p＜q，故p既是质数又是偶数，于是p=2．

例2设p（≥5）是质数，并且2p+1也是质数．求证：

4p+1是合数．

证由于p是大于3的质数，故p不会是3k的形式，从而p必定是3k+1或3k+2的形式，k是正整数．