安徽省皖江名校联盟学年高三上学期第一次联考数学理试题.docx

安徽省皖江名校联盟学年高三上学期第一次联考数学理试题.docx

《安徽省皖江名校联盟学年高三上学期第一次联考数学理试题.docx》由会员分享，可在线阅读，更多相关《安徽省皖江名校联盟学年高三上学期第一次联考数学理试题.docx（28页珍藏版）》请在冰豆网上搜索。

安徽省皖江名校联盟学年高三上学期第一次联考数学理试题

安徽省皖江名校联盟2020-2021学年高三上学期第一次联考数学（理）试题

学校:

___________姓名：

___________班级：

___________考号：

___________

一、单选题

1．函数定义域和值域分别为、，则=（）

A．[-1，3]B．[-1，4]C．[0，3]D．[0，2]

2．复数满足，则（）

A．B．C．D．

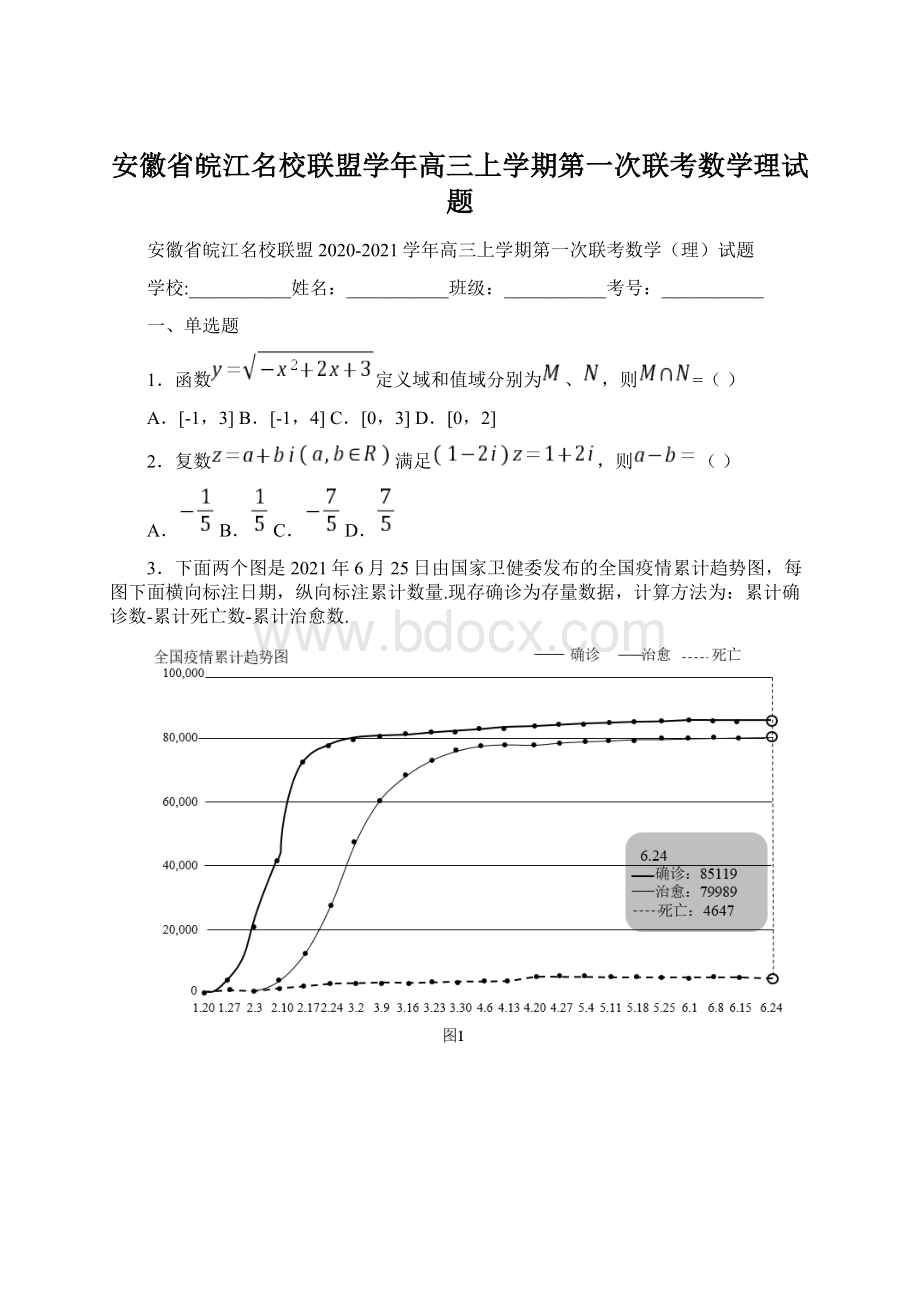
3．下面两个图是2021年6月25日由国家卫健委发布的全国疫情累计趋势图，每图下面横向标注日期，纵向标注累计数量.现存确诊为存量数据，计算方法为：

累计确诊数-累计死亡数-累计治愈数.

则下列对新冠肺炎叙述错误的是（）

A．自1月20日以来一个月内，全国累计确诊病例属于快速增长时期

B．自4月份以来，全国累计确诊病例增速缓慢，疫情扩散势头基本控制

C．自6月16日至24日以来，全国每日现存确诊病例平缓增加

D．自6月16日至24日以来，全国每日现存确诊病例逐步减少

4．已知，，，则（）

A．B．C．D．

5．疫情期间部分中小学进行在线学习，某市教育局为了解学生线上学习情况，准备从10所学校（其中6所中学4所小学）随机选出3所进行调研，其中中学与小学同时被选中的概率为（）

A．B．C．D．

6．函数的部分图象大致为（）

A．B．

C．D．

7．祖冲之是中国古代数学家、天文学家，他将圆周率推算到小数点后第七位.利用随机模拟的方法也可以估计圆周率的值，如图程序框图中rand（）表示产生区间上的随机数，则由此可估计的近似值为（）

A．B．C．D．

8．已知双曲线：

的右顶点为，任意一条平行于轴的直线交于，两点，总有，则双曲线的离心率为（）

A．B．C．D．

9．从一张圆形铁板上剪下一个扇形，将其制成一个无底圆锥容器，当容器体积最大时，该扇形的圆心角是（）

A．B．C．D．

10．数列满足：

，，若数列的前项和，则最小为（）

A．6B．7C．8D．9

11．已知函数，则下列结论正确的是（）

A．的最小正周期为B．的最大值为

C．的图象关于对称D．的图象关于对称

12．在棱长为1的正方体中，，分别为棱，的中点.平面过，两点，且.设平面截正方体所得截面面积为，且将正方体分成两部分的体积比为，有如下结论：

①，②，③，④，则下列结论正确的是（）

A．①③B．①④C．②③D．②④

二、填空题

13．曲线在处的切线方程为______.

14．已知单位向量，满足，则与的夹角为________.

15．由数列和的公共项组成的数列记为，已知，，若为递增数列，且，则=________.

16．已知抛物线的焦点为，准线为，：

过点且与相切，轴被所截得的弦长为4，则=________.

三、解答题

17．在中，角，，的对边分别为，，，，.

（1）求；

（2）若边上中线，求的周长.

18．如图，在三棱锥中，，，侧面底面.

（1）求证：

是直角三角形；

（2）若，求二面角的余弦值.

19．已知某工厂有甲乙两条互不影响的生产线，同时生产一种内径为的零件.为了对它们生产质量进行检测，分别从生产的零件中随机抽取部分零件绘成频率分布直方图如下：

（1）从直方图中数据均值说明哪条生产线加工零件精确度更高?

（同一组中的数据用该组区间的中点值为代表）

（2）记加工的零件内径尺寸落在[25.38，25.42）的零件为一等品，零件内径尺寸落在[25.42，25.50]的为二等品，零件内径尺寸落在[25.30，25.38）的为三等品，每个零件一等品、二等品和三等品的利润分别为200元、100元和50元.

①从两条生产线生产的零件中分别取一个零件，求甲生产线上零件精度等级高于乙生产线上零件等级的概率；

②现有10000个零件需要加工，其中甲生产线加工个，乙生产线加工个，以工厂利润的期望为决策依据，在和之中选其一，应选哪种方案使工厂的利润最大?

20．在中，已知，，直线与的斜率之积为，记动点的轨迹为曲线.

（1）求曲线的方程；

（2）设为曲线上一点，直线与交点的横坐标为4，求证：

直线过定点.

21．已知函数.

（1）讨论的单调性；

（2）若，求实数的取值范围.

22．在平面直角坐标系中，直线过定点且倾斜角为.以为极点，轴的正半轴为极轴，建立极坐标系，曲线的极坐标方程为.

（1）求曲线的直角坐标方程；

（2）已知直线交曲线于，两点，且，求的参数方程.

23．已知不等式的解集为.

（1）求；

（2）若、、，且，求证：

.

参考答案

1．D

【分析】

先求出函数的定义域和值域,得到集合、，再求交集即可.

【详解】

解:

要使函数有意义,

则解得，

故；

由，

所以.故.

则选:

D

【点睛】

本题考查函数的定义域和值域的求法,考查集合的交集运算,是简单题.

2．C

【分析】

由复数除法计算出，然后由复数的定义写出可得其差．

【详解】

由已知，，，

则，

故选：

C．

【点睛】

本题考查复数的除法，复数的概念，属于基础题．

3．D

【分析】

根据图象逐项分析即可.

【详解】

由图一可知A，B均正确.

由图二数据计算得16的现存确诊病例为，

同理可计算18、20、22、24日现存确诊分别为346，383，441，473，

故选：

D

【点睛】

本题考查学生合情推理的能力，数形结合思想，属于基础题.

4．A

【分析】

根据指数函数，对数函数的单调性判断即可；

【详解】

解：

由已知，，

，．，故，

故选：

A.

【点睛】

本题考查指数函数、对数函数的性质的应用，属于基础题.

5．C

【分析】

根据题意，得到总的基本事件个数，以及满足条件的基本事件个数，基本事件的个数比，即为所求概率.

【详解】

从10所学校（其中6所中学4所小学）随机选出3所，所包含的基本事件共个，

其中中学与小学被选中包含个基本事件，

故所求概率为.

故选：

C.

【点睛】

本题主要考查求古典概型的概率，熟记概率计算公式即可，属于基础题型.

6．C

【分析】

根据函数的解析式，求得，得到为奇函数，再结合，即可求解.

【详解】

由题意，函数，

可得函数的定义域为关于原点对称，

又由，即，

故为奇函数，排除A、B；

又由，排除D.

故选：

C.

【点睛】

本题主要考查了根据函数图象的识别，其中解答中熟练应用函数的奇偶性，以及特殊点的函数值进行求解是解答的关键，着重考查推理与运算能力.

7．D

【分析】

在上产生1000对随机数得到点，当时将点的个数累加得到输出值，即可类比为在一个边长为1的正方形中随机产生点，点在以正方形的两边为半径的扇形内的概率等于扇形面积与正方形面积之比即可求的近似值；

【详解】

由程序框图可知，落在正方形内的1000个点，其中落在圆内有（如图），

所以，故，故选：

D.

【点睛】

本题考查了程序流程图、概率，由程序流程图理解应用随机数的几何含义，结合概率与几何图形的面积关系求的近似值；

8．D

【分析】

设，，由可得，对于或恒成立，可得，即可得答案；

【详解】

设，，则，又，

，，由已知，则，

即，对于或恒成立，故，即，

所以.

故选:

A.

【点睛】

本题考查椭圆离心率的求解，考查逻辑推理能力、运算求解能力.

9．D

【分析】

设圆锥的底面半径为，高为，，体积为，求出，表示出体积表达式，利用导数求出函数的最大值，得到结果.

【详解】

解:

设圆锥底面半径为，高为，则，

圆锥的体积为，

，得，

此时圆锥体积最大.故，

由，

故选:

D

【点睛】

本题考查圆锥与扇形展开图的关系体积的计算考查计算能力，导数的应用，必须注意函数的单调性与最值的关系.

10．B

【分析】

根据，，令m=1,得到，再利用累加法求得，进而得到，再利用裂项相消法求解.

【详解】

因为，，

所以，

所以，

所以,

，

所以，

所以，

，

因为，

所以，

解得，

故选：

B.

【点睛】

本题主要考查累加法求通项公式等差数列求和公式以及裂项相消法求和，还考查了运算求解的能力，属于中档题.

11．B

【分析】

根据题意函数不能简化为的形式,

代入特殊点来验证可知的最小正周期不为,的图象也不关于对称

图象不关于对称,结合导数可得的最大值为.

【详解】

解:

因为函数不能简化为的形式,

故最小正周期需要代入特殊点来验证.

，，，故的最小正周期不为,故A错误;

的图象也不关于对称,故D错误;

因为，，故C错误.

令,即或,

当，时，，

当，时,

当，时，，

故,,故B正确.

故选:

B

【点睛】

本题考查三角函数的对称性和周期性,考查函数的最值,属于中档题.

12．D

【分析】

先证明平面即平面.截面为等腰梯形，结合，，，高，可得面积.再根据几何体为棱台，结合上底面积，下底面积，高，可得体积，则，即可得出.从而得出正确答案.

【详解】

解:

取的中点，连接，，，，，

可得，则，故平面即平面.

故截面为等腰梯形，可得，，，

高为，其面积.故①错误,②正确.

另几何体为棱台，上底面积，下底面积，高，

故体积，

另一部分体积，

所以.故③错误,④正确.

故选:

D

【点睛】

本题考查几何体的面积以及体积的运算,考查空间思维和运算能力,属于中档题.

13．

【分析】

由题意知切点为，根据导数的几何意义求切线的斜率，即可得切线方程；

【详解】

，.又曲线过点，故切线方程为.

故答案为：

；

【点睛】

本题考查了利用导数的几何意义求切线方程，首先由切点在曲线上求点坐标，进而由该点导数的几何意义求斜率，写出切线方程，属于简单题；

14．

【分析】

由单位向量，满足，化简得，再结合向量的夹角公式，即可求解.

【详解】

由单位向量，满足，可得，

又因为，可得，

设向量与的夹角为，且，

因为，所以.

故答案为：

.

【点睛】

本题主要考查了平面向量的数量积的运算，以及向量的夹角公式的应用，其中解答中熟记向量的数量积的运算公式是解答的关键，着重考查推理与运算能力.

15．352

【分析】

由已知，设，逐一推导下一项有等量关系的和的值，得到，从而求出时和的值.

【详解】

由已知，设，即，

，不是正整数，所以不是公共项.

，故，

因为，所以，，，，

故当时，，，故.

故答案为:

【点睛】

本题考查等差和等比数列的应用，考查递推关系的应用，考查学生的分析能力和推导能力，属于难题.

16．1或3

【分析】

根据题意，得到圆心在抛物线上，推出；再由抛物线的定义，得到；联立求出；再由圆的性质，由题中条件，得出，进而可求出，从而可求出.

【详解】

由已知得圆心在抛物线上，所以；

又抛物线上的点到焦点的距离等于到准线的距离，则，

所以，

因为轴被所截得的弦长为，

根据圆的性质：

圆心到弦的距离的平方，与弦长一半的平方之和，等于半径的平方；

所以，故.

所以，即，所以或，故或.

故答案为：

1或3.

【点睛】

本题主要考查抛物线的方程与抛物线定义的应用，考查由圆的弦长求参数，属于常考题型.

17．

（1）；

（2）.

【分析】

（1）根据题设条件，利用正弦定理和三角形内角和定理化简得，

求得，再结合两角和的余弦公式，即可求解.

（2）由

（1）和正弦定理求得，设，再由余弦定理，列出方程求得的值，进而求得三角形的周长.

【详解】

（1）因为，由正弦定理得，

由，则，

代入上式得，

又由，可得，故，所以，

又因为，所以.

（2）由

（1）知，，可得

由正弦定理，可得，

设，

在中，由余弦定理得