全等三角形的判定压轴题.docx

全等三角形的判定压轴题.docx

《全等三角形的判定压轴题.docx》由会员分享，可在线阅读，更多相关《全等三角形的判定压轴题.docx（47页珍藏版）》请在冰豆网上搜索。

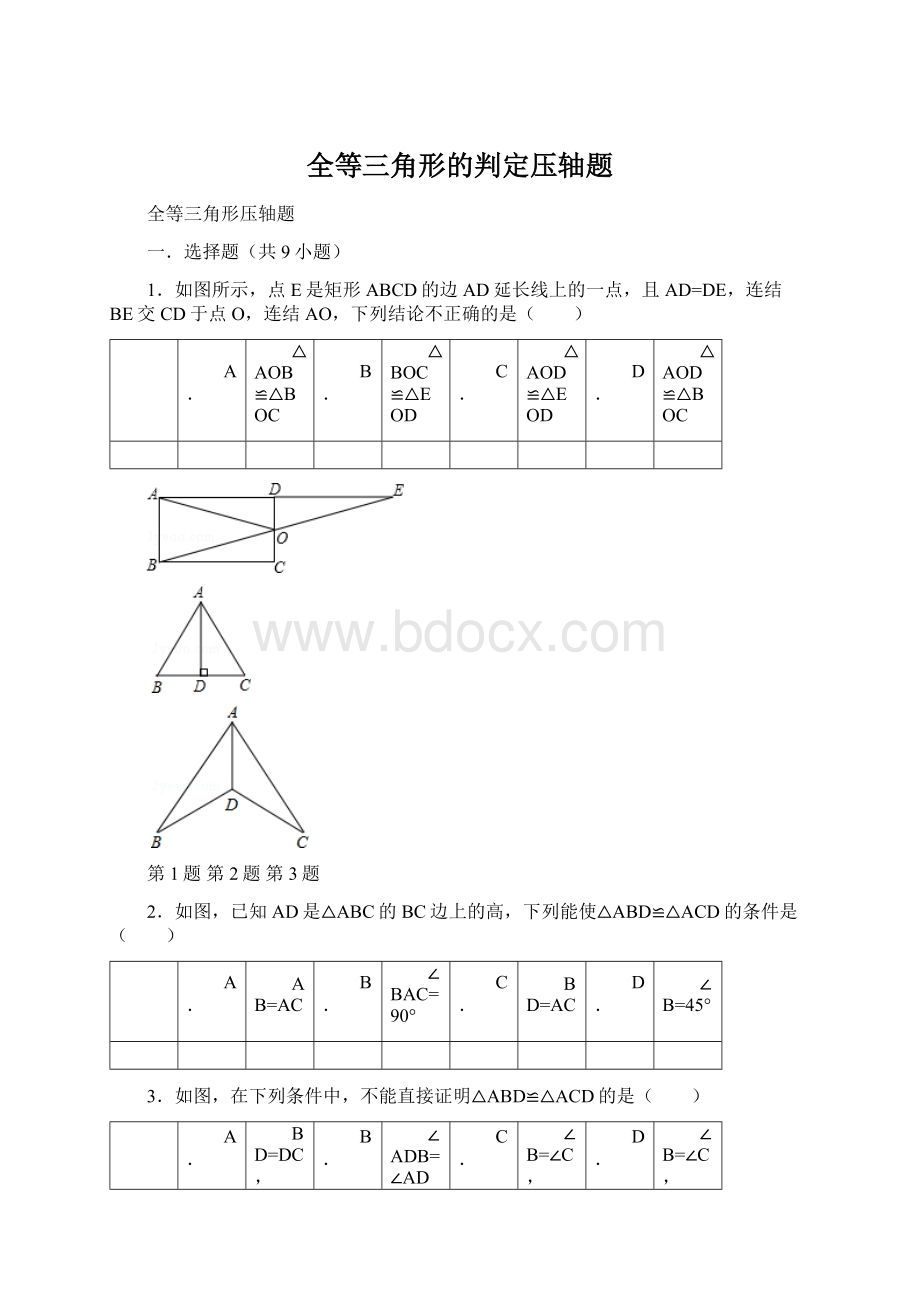
全等三角形的判定压轴题

全等三角形压轴题

一．选择题（共9小题）

1．如图所示，点E是矩形ABCD的边AD延长线上的一点，且AD=DE，连结BE交CD于点O，连结AO，下列结论不正确的是（　　）

A．

△AOB≌△BOC

B．

△BOC≌△EOD

C．

△AOD≌△EOD

D．

△AOD≌△BOC

第1题第2题第3题

2．如图，已知AD是△ABC的BC边上的高，下列能使△ABD≌△ACD的条件是（　　）

A．

AB=AC

B．

∠BAC=90°

C．

BD=AC

D．

∠B=45°

3．如图，在下列条件中，不能直接证明△ABD≌△ACD的是（　　）

A．

BD=DC，AB=AC

B．

∠ADB=∠ADC，BD=DC

C．

∠B=∠C，BAD=∠CAD

D．

∠B=∠C，BD=DC

4．如图，点B、C、E在同一条直线上，△ABC与△CDE都是等边三角形，则下列结论不一定成立的是（　　）

A．

△ACE≌△BCD

B．

△BGC≌△AFC

C．

△DCG≌△ECF

D．

△ADB≌△CEA

第4题第5题第6题

5．在直角梯形ABCD中，AD∥BC，∠ABC=90°，AB=BC，E为AB边上一点，∠BCE=15°，且AE=AD．连接DE交对角线AC于H，连接BH．下列结论：

①△ACD≌△ACE；②△CDE为等边三角形；③

=2；④

．

其中结论正确的是（　　）

A．

只有①②

B．

只有①②④

C．

只有③④

D．

①②③④

6．如图所示，正方形ABCD中，点E是CD边上一点，连接AE，交对角线BD于点F，连接CF，则图中全等三角形共有（　　）

A．

1对

B．

2对

C．

3对

D．

4对

7．下列命题：

①有两个角和第三个角的平分线对应相等的两个三角形全等；②有两条边和第三条边上的中线对应相等的两个三角形全等；③有两条边和第三条边上的高对应相等的两个三角形全等．其中正确的是（　　）

A．

①②

B．

②③

C．

①③

D．

①②③

8．根据下列已知条件，能唯一画出△ABC的是（　　）

A．

AB=3，BC=4，AC=8

B．

AB=4，BC=3，∠A=30°

C．

∠A=60°，∠B=45°，AB=4

D．

∠C=90°，AB=6

9．如图，AB，CD相交于点E，且AB=CD，试添加一个条件使得△ADE≌△CBE．现给出如下五个条件：

①∠A=∠C；②∠B=∠D；③AE=CE；④BE=DE；⑤AD=CB．其中符合要求有（　　）

A．

2个

B．

3个

C．

4个

D．

5个

第9题第10题第11题

二．填空题（共7小题）

10．如图，△ABC≌△DEF，请根据图中提供的信息，写出x=　_________　．

11．如图，已知∠1=∠2=90°，AD=AE，那么图中有　_________　对全等三角形．

12．如图，在△ABC和△BAD中，BC=AD，请你再补充一个条件，要使△ABC≌△BAD．你补充的条件是　_________　（只填一个）．

第12题第14题第15题

13．已知△ABC中，AB=BC≠AC，作与△ABC只有一条公共边，且与△ABC全等的三角形，这样的三角形一共能作出　_________　个．

14．如图，△ABC中，D，E，F分别是AB，BC，AC上的点，已知DF∥BC，EF∥AB，请补充一个条件：

　_________　，使△ADF≌△FEC．

15．如图EB交AC于M，交FC于D，AB交FC于N，∠E=∠F=90°，∠B=∠C，AE=AF．给出下列结论：

①∠1=∠2；②BE=CF；③△ACN≌△ABM；④CD=DN．其中正确的结论有　_________　（填序号）．

16．如图：

△ABC中，AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，请你添加一个适当的条件：

　_________　，使△ABD≌△CBE．

三．解答题（共8小题）

17．如图，已知AB=CD，∠B=∠C，AC和BD相交于点O，E是AD的中点，连接OE．

（1）求证：

△AOB≌△DOC；

（2）求∠AEO的度数．

18．△ABC是等边三角形，点D是射线BC上的一个动点（点D不与点B、C重合），△ADE是以AD为边的等边三角形，过点E作BC的平行线，分别交射线AB、AC于点F、G，连接BE．

（1）如图（a）所示，当点D在线段BC上时．

①求证：

△AEB≌△ADC；

②探究四边形BCGE是怎样特殊的四边形？

并说明理由；

（2）如图（b）所示，当点D在BC的延长线上时，直接写出

（1）中的两个结论是否成立；

（3）在

（2）的情况下，当点D运动到什么位置时，四边形BCGE是菱形？

并说明理由．

19．在△ABC中，AB=AC，点D是直线BC上一点（不与B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．

（1）如图1，当点D在线段BC上，如果∠BAC=90°，则∠BCE=　_________　度；

（2）设∠BAC=α，∠BCE=β．

①如图2，当点D在线段BC上移动，则α，β之间有怎样的数量关系？

请说明理由；

②当点D在直线BC上移动，则α，β之间有怎样的数量关系？

请直接写出你的结论．

20．请阅读，完成证明和填空．

九年级数学兴趣小组在学校的“数学长廊”中兴奋地展示了他们小组探究发现的结果，内容如下：

（1）如图1，正三角形ABC中，在AB、AC边上分别取点M、N，使BM=AN，连接BN、CM，发现BN=CM，且∠NOC=60度．请证明：

∠NOC=60度．

（2）如图2，正方形ABCD中，在AB、BC边上分别取点M、N，使AM=BN，连接AN、DM，那么AN=　_________　，且∠DON=　_________　度．

（3）如图3，正五边形ABCDE中，在AB、BC边上分别取点M、N，使AM=BN，连接AN、EM，那么AN=　_________　，且∠EON=　_________　度．

（4）在正n边形中，对相邻的三边实施同样的操作过程，也会有类似的结论．

请大胆猜测，用一句话概括你的发现：

　_________　．

21．已知，如图，延长△ABC的各边，使得BF=AC，AE=CD=AB，顺次连接D，E，F，得到△DEF为等边三角形．求证：

（1）△AEF≌△CDE；

（2）△ABC为等边三角形．

22．如图，在正方形ABCD中，E是CD边的中点，AC与BE相交于点F，连接DF．

（1）在不增加点和线的前提下，直接写出图中所有的全等三角形；

（2）连接AE，试判断AE与DF的位置关系，并证明你的结论；

（3）延长DF交BC于点M，试判断BM与MC的数量关系．（直接写出结论）

23．我们知道，两边及其中一边的对角分别对应相等的两个三角形不一定全等．那么在什么情况下，它们会全等？

（1）阅读与证明：

对于这两个三角形均为直角三角形，显然它们全等．

对于这两个三角形均为钝角三角形，可证它们全等（证明略）．

对于这两个三角形均为锐角三角形，它们也全等，可证明如下：

已知：

△ABC、△A1B1C1均为锐角三角形，AB=A1B1，BC=B1Cl，∠C=∠Cl．

求证：

△ABC≌△A1B1C1．

（请你将下列证明过程补充完整．）

证明：

分别过点B，B1作BD⊥CA于D，

B1D1⊥C1A1于D1．

则∠BDC=∠B1D1C1=90°，

∵BC=B1C1，∠C=∠C1，

∴△BCD≌△B1C1D1，

∴BD=B1D1．

（2）归纳与叙述：

由

（1）可得到一个正确结论，请你写出这个结论．

24．如图，已知矩形ABCD中，E是AD上的一点，F是AB上的一点，EF⊥EC，且EF=EC，

求证：

△CDE≌△EAF．

参考答案与试题解析

一．选择题（共9小题）

1．如图所示，点E是矩形ABCD的边AD延长线上的一点，且AD=DE，连结BE交CD于点O，连结AO，下列结论不正确的是（　　）

A．

△AOB≌△BOC

B．

△BOC≌△EOD

C．

△AOD≌△EOD

D．

△AOD≌△BOC

考点：

全等三角形的判定；矩形的性质．菁优网版权所有

专题：

压轴题．

分析：

根据AD=DE，OD=OD，∠ADO=∠EDO=90°，可证明△AOD≌△EOD，OD为△ABE的中位线，OD=OC，然后根据矩形的性质和全等三角形的性质找出全等三角形即可．

解答：

解：

∵AD=DE，DO∥AB，

∴OD为△ABE的中位线，

∴OD=OC，

∵在△AOD和△EOD中，

，

∴△AOD≌△EOD（SAS）；

∵在△AOD和△BOC中，

，

∴△AOD≌△BOC（SAS）；

∵△AOD≌△EOD，

∴△BOC≌△EOD；

故B、C、D均正确．

故选A．

点评：

本题考查了全等三角形的判定，判定两个三角形全等的一般方法有：

SSS、SAS、ASA、AAS、HL．注意：

AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．

2．如图，已知AD是△ABC的BC边上的高，下列能使△ABD≌△ACD的条件是（　　）

A．

AB=AC

B．

∠BAC=90°

C．

BD=AC

D．

∠B=45°

考点：

全等三角形的判定．菁优网版权所有

专题：

压轴题．

分析：

此题是开放型题型，根据题目现有条件，AD=AD，∠ADB=∠ADC=90°，可以用HL判断确定，也可以用SAS，AAS，SSS判断两个三角形全等．

解答：

解：

添加AB=AC，符合判定定理HL；

添加BD=DC，符合判定定理SAS；

添加∠B=∠C，符合判定定理AAS；

添加∠BAD=∠CAD，符合判定定理ASA；

选其中任何一个均可．

故选：

A．

点评：

本题主要考查了学生对三角形全等判断的几种方法的应用能力，既可以用直角三角形全等的特殊方法，又可以用一般方法判定全等，关键是熟练掌握全等三角形的判定定理．

3．如图，在下列条件中，不能直接证明△ABD≌△ACD的是（　　）

A．

BD=DC，AB=AC

B．

∠ADB=∠ADC，BD=DC

C．

∠B=∠C，∠BAD=∠CAD

D．

∠B=∠C，BD=DC

考点：

全等三角形的判定．菁优网版权所有

专题：

压轴题．

分析：

两个三角形有公共边AD，可利用SSS，SAS，ASA，AAS的方法判断全等三角形．

解答：

解：

∵AD=AD，

A、当BD=DC，AB=AC时，利用SSS证明△ABD≌△ACD，故正确；

B、当∠ADB=∠ADC，BD=DC时，利用SAS证明△ABD≌△ACD，故正确；

C、当∠B=∠C，∠BAD=∠CAD时，利用AAS证明△ABD≌△ACD，故正确；

D